内孔不穿丝工艺的可行性分析

CVD金刚石薄膜的沉积包括三个主要步骤，分别是反应气体在热丝周围的分解，分解生成的活性基团向基体表面转移以及基体表面的化学反应。DTNFTH中，气体分解同样是在高温热丝周围完成的，可直接通过热丝功率的调整来控制。在低压环境下，从高温热丝向相对低温区域的热辐射是反应环境及基体热量的主要来源，因此本节研究中首先基于面对面辐射模型对辐射强度进行计算，计算示意如图6-33（a）所示，热辐射角系数定义如下：

式中，θi和θj分别为面单元d Ai或d Aj法向与两面连线的夹角；L为两面间距；d Aj为面单元的面积。

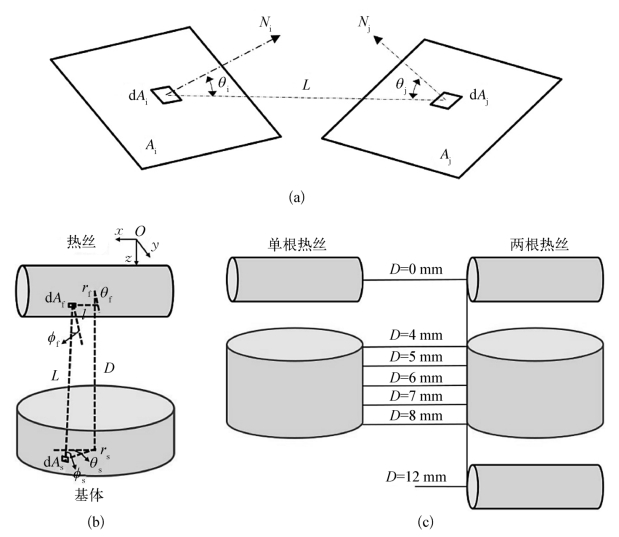
图6-33　（a）面对面辐射模型，（b）DTNFTH工艺中单根热丝向内孔表面的辐射及（c）DTNFTH工艺中单根或两根热丝的排布示意

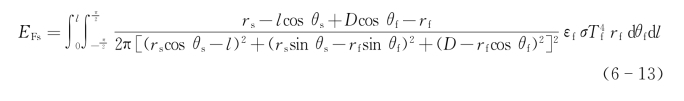
首先采用最简单的应用单根热丝的DTNFTH模型［见图6-33（b）］计算从d Af到d As的辐射强度，然后通过双重积分可以得到从热丝下半侧表面Af到内孔表面某面单元d As的总辐射强度EFs，计算公式如下：式中，l为热丝长度；rf为热丝半径；rs为内孔半径；D为从热丝中心线到内孔参考面的垂直距离；εf为钽丝的表面辐射系数（0.38）；σ为斯特藩-玻尔兹曼常数［5.67×10－8 W/（m2·K4）］；Tf为热丝的绝对温度。所有其他参数如图6-33（b）所示。采用一种典型情况（l＝2 mm，rf＝0.2 mm，rs＝1 mm，Tf＝1 073.15 K）作为示例，计算得到的内孔表面不同位置的辐射强度EFs如图6-34所示，可知EFs随D的增加而下降。对应的不同参考截面（不同D）上的EFs的偏差如表6-18所示。在相同的参考截面上的EFs的偏差很小，这说明沿周向方向的辐射相对比较均匀，这对于在金刚石薄膜沉积过程中保证薄膜厚度均匀性和内孔圆度具有重要作用。但是随着D的增加，EFs会迅速下降，虽然固体部件中的热传导作用或其他辅助夹具的应用可以进一步使内孔表面温度趋于均匀，但是采用单根热丝的简单DTNFTH模型从原理上来讲很难提供均匀的辐射强度和基体温度分布。将基体置于两根热丝之间的模型如图6-33（c）所示，在该情况下，内孔表面沿轴向方向的EFs从88.8%下降到50.14%，可以起到一定的改善辐射强度和基体温度分布均匀性的作用。

图6-34　DTNFTH工艺中单根热丝对内孔表面不同位置的辐射强度犈Fs

在辐射分析基础上，继续采用前文所述的仿真模型，综合考虑热传导、热对流和热辐射的作用研究内孔表面的温度分布，结果如图6-35所示。该仿真中采用的基体尺寸为φ4 mm×4 mm，内孔尺寸为φ2 mm×4 mm，d1和d2均设定为0.4 mm，调整D1和D2（对于单根热丝，只有d1和D1）以使内孔表面最高温度维持在800℃左右，以便直观地对比内孔表面的温度偏差。采用相同的如图6-32所示的基体夹具时，把基体置于两根热丝中间（A型）相比于只采用一根热丝（B型）可以提供明显更为均匀的温度分布。而当不采用基体夹具、直接将基体置于工作台上（C型）时内孔表面的温度分布更不均匀。此外，对于A型和B型而言，其内孔表面温度分布的趋势和表6-18所示辐射强度分布的趋势类似，但是温度偏差没有辐射强度偏差显著，这是因为在辐射强度计算中忽略了所有其他传热途径，尤其是基体自身和基体夹具的热传导作用。

图6-35　采用图6-32所示夹具并将（a）基体置于两根热丝中间及（b）基体置于单根热丝下时的内孔表面温度场分布，（c）采用单根热丝且直接将基体置于工作台上时的内孔表面温度场分布

表6-18　采用单根或两根热丝进行不穿丝沉积时计算得到的辐射强度数值

在我们以往的研究中已经指出，热丝和基体温度除了可通过热丝加热直接控制外，还可以通过采用辅助夹具或辅助散热的方式进行调整［121］。金刚石薄膜沉积过程中的化学反应（主要是氢原子在基体表面的复合反应）也会对基体温度有明显影响。此外，移动到基体表面的活性基团的数量（主要是氢原子和CHx基团）还会对金刚石薄膜的生长产生直接影响。在活性基团从热丝向基体表面的运动过程中，平均自由程对于活性基团的碰撞和复合概率起到决定性作用，典型基团的近似平均自由程如表6-19所示，即使是在较低的反应压力（1 000 Pa）和较高的温度（2 300℃）下，最大的平均自由程数值也仅有0.8 mm，随着反应压力的增加和温度的下降，平均自由程会更小，也就是说所有基团的平均自由程都要比热丝-基体间距小一个数量级，在该情况下，虽然部分活性基团会在运动过程中碰撞复合，但仍然可以有足够的活性基团到达基体表面（大量的沉积试验证明了这一点），但是随着热丝-基体间距的增加，能够达到基体表面的活性基团数量会迅速减少，我们将之称为“距离效应”。此外，在DTNFTH中，活性基团的运动还有别于内孔穿丝工艺（deposition technology with filament through hole，DTFTH），因为通过简单的几何分析可知，该情况下内孔表面部分区域会被基体本身遮挡住，也就是在基体周围分解生成的活性基团没有办法直线运动到这些区域表面，我们称之为“遮挡效应”。从这一角度出发，两根热丝有助于缩短基体内孔下半部到热丝的距离，并且破除部分的遮挡效应，因此更有利于保证内孔表面温度场分布及薄膜沉积的均匀性。(www.xing528.com)

表6-19　与金刚石薄膜沉积相关的典型分子、原子及官能团的近似平均自由程（单位：mm）

图6-36　（a）拉拔模具结构示意图及（b）采用模套结构的优化设计的拉拔模具

基于上述双热丝模型，我们以传统结构不锈钢拉丝模为例，进一步分析DTNFTH的可行性和限制性，拉丝模结构示意如图6-36（a）所示，具体的尺寸参数为：d＝2 mm，H＝14 mm，Ds＝16 mm，h1＝1 mm，h2＝5 mm，h3＝2 mm，α1＝20°，α2＝40°，α3＝90°。采用的沉积参数（MCD）如表6-20所示，热丝直径d1和d2均设定为0.4 mm，D1和D2设定为3 mm，据此制备的金刚石薄膜涂层拉拔模具的照片如图6-37（a）所示，包括沉积过程中测量得到的三个典型位置的温度数值，与前文所述仿真结果趋势一致。位置3的表面形貌如图6-37（b）所示，而位置1和2的截面形貌如图6-37（c）和（d）所示。在该试验中，金刚石薄膜不能完全覆盖内孔表面，在如图6-37（a）所示两条红线之间的区域只有散布的金刚石晶粒，没有形成连续的金刚石薄膜。但是从图6-37（b）可以看出，虽然金刚石晶粒大小只有不到500 nm，但是整体的形核密度较高，这是因为虽然“距离效应”和“遮挡效应”同样会影响到形核过程，没有足够的活性基团就不能保证形核速率和形核密度，但是在长达8 h的整个沉积过程中（不仅仅是形核阶段），断断续续到达中间区域的活性基团仍然会继续参与形核，但是由于缺乏活性基团，薄膜生长极其缓慢，没有办法形成连续的金刚石薄膜。如图6-37（c）和（d）所示，即便是在薄膜连续的区域，薄膜厚度也存在明显差距，随热丝-基体间距的增加，薄膜厚度会显著减小。

表6-20　沉积试验基本参数

图6-37　采用DTNFTH工艺制备的金刚石薄膜涂层拉拔模具（a）照片，（b）位置3的表面形貌及（c）位置1和（d）位置2的截面形貌

某些研究认为热阻塞和热绕流也会对金刚石薄膜的生长有明显影响，而强制气体对流（forced gas convection，FGC）技术可以打破热阻塞或热绕流，从而促进反应气体到达基体表面。如图6-38（a）所示为在采用典型的FGC（入气口靠近上方热丝）情况下模拟得到的气体流场分布。在该情况下，整个内孔区域的流速也低于0.01 m/s，热阻塞效应非常明显，可以等效影响整个内孔区域，这并不能够解释为什么内孔表面金刚石薄膜的生长速率存在明显差异。这是因为宏观的气体流速与微观的基团运动速度相差几个数量级，而活性基团从热丝周围运动到基体表面主要依靠的是扩散质量输送而非气体对流。针对NTNFTH特殊工况设计了专用的FGC夹具并同样进行了试沉积试验，该夹具示意图如图6-38（b）所示，气体直接通入该夹具内部，并且必须通过基体内孔区域才能流出，因此有效保证了内孔区域的气体流速。但是在该情况下的沉积结果类似于前面试验的结果，在中间区域仍然没有连续的金刚石薄膜生成，并且无连续薄膜区域的边界也基本没有变化。这进一步证明了活性基团从热丝向基体的运动主要依赖的是扩散质量输送，而与强制对流带来的气体流速的增加关系不大。

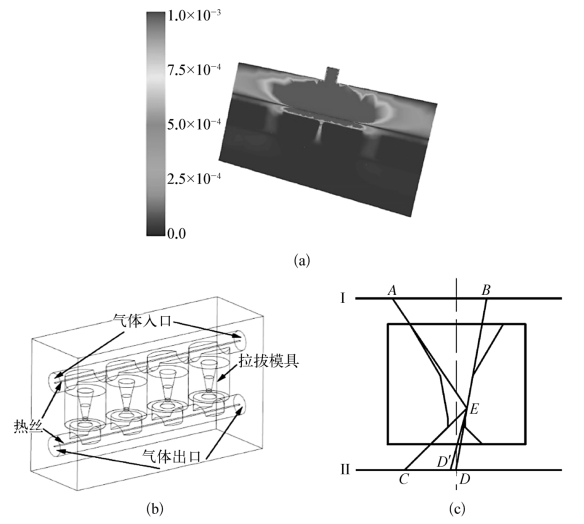
图6-38　（a）采用强制气体对流（FGC）工艺情况下的典型流场分布（单位：m/s），（b）实施FGC的特制夹具，（c）用于分析“遮挡效应”及“距离效应”的示意

内孔表面温度场分布的不均匀会对金刚石薄膜生长的均匀性造成直接影响，但是这依旧不能解释为什么会有非连续薄膜区域的存在，因为通过仿真和测温结果可知，这部分区域的温度（700℃左右）可以满足金刚石薄膜的生长要求。归根结底，可以解释非连续薄膜区域存在的唯一原理就是“遮挡效应”和“距离效应”。如图6-38（b）所示，以E点作为研究对象，从该点到热丝II的垂直距离小于8 mm，该距离已经远大于大多数活性基团的平均自由程，但是通过大部分以往研究表明，该距离还是可以满足金刚石薄膜的生长需求，但是热丝II上可以直接照射到E点的区域只有C至D；从E点到热丝I的垂直距离大于12 mm，实际距离更大，因此从热丝I附近移动到E点的活性基团数量会很少。此外，较小的射入角度（比如从D′点到E点）也不利于活性基团从热丝周围移动到基体表面。总而言之，内孔表面部分区域没有充足的活性基团供应，在遮挡、热丝-基体间距以及基体表面温度的综合作用下导致非连续薄膜区域的出现。根据图6-37（a）及类似试验结果（采用同类基体，D1和D2从3 mm变到6 mm），非连续薄膜区域深度一直处在3～4 mm的范围内，距离入口端面6～6.5 mm，距离出口端面4～4.5 mm。

综上所述，DTNFTH并不适用于所有内孔表面金刚石薄膜的沉积，为了尽量减少遮挡和距离效应的影响，避免非连续薄膜区域的出现，内孔的深径比不能大于4，并且越小越好，因此实际拉拔模具的内孔形状可基于该原则进行改进设计，拉拔模具的典型结构包括入口区、压缩区、定径区和出口区，如图6-36（a）所示。通过以往研究证明，定径区的长度和压缩区的角度对于控制产品的尺寸精度和应力分布至关重要，这两个参数可以通过有限元仿真进行优化，并且必须控制在一定合适的范围内。入口区主要用于引入润滑油，不与线材直接接触，出口区也不与线材直接接触，因此这两个区域的长度可以大幅缩短。此外，在增大α2的基础上，压缩区长度也可以合理缩短。基于上述原则，重新设计的用于不锈钢丝拉拔的模具尺寸参数如下：d＝2 mm，H＝6 mm，Ds＝8 mm，h1＝1 mm，h2＝2 mm，h3＝1 mm，α1＝16°，α2＝50°，α3＝90°。因为该模具的外形尺寸不能满足拉丝设备的需求，因此在沉积金刚石薄膜后，再在模具外面镶套模套，其结构示意如图6-36（b）所示。