1)热丝参数影响性分析
基于前文所述的等边三角形及由此拓展而来的等边多边形热丝排布和已有的内孔金刚石薄膜沉积仿真模型及方法,本节首先以φ80 mm的SiC基体内孔为例,研究热丝排布参数对于内孔表面温度场分布的影响规律,初始基本模型如图6-12所示,采用的基本材料参数如表6-5所示。热丝排布参数定义如图6-13所示,其中,N为热丝数量,α为排布方向,Tf为热丝温度,df为热丝直径,rc为热丝排布圆周半径,h为热丝整体向下偏移的距离。初始的热丝排布参数如下:N=6,α=30°,Tf=2 100℃,df=1 mm,rc=25 mm,h=0。反应气体定义为纯氢气,流量为1 150 mL/min,反应压力为5 000 Pa,所有水冷壁面的表面对流系数定义为55 W/(m2·℃)。在初始条件下的仿真结果及对应的测温结果如图6-14(a)所示,内孔表面的温度数值达到金刚石薄膜生长的要求,但是温差高达30℃,高温区位于模具上方,低温区位于模具下方,这主要是因为模具内孔不同位置与下方水冷工作台的距离不同,因此传导散热速率存在明显差别。此外,测温结果与仿真结果的规律一致,误差约为4%。

图6-12 大孔径内孔金刚石薄膜沉积的初始基本模型
在初始模型计算前及计算过程中进行了以下简化:
(1)实际设备中的冷却水用水冷壁面上的表面对流系数代替,实际设备中的冷却水流量约为10 mL/s,对应的仿真结果如图6-14(b)所示,与图6-14(a)中的仿真结果基本一致。仿真计算中如果考虑实际的冷却水流动,会大幅增加计算量,甚至很容易导致计算发散,因此在后文仿真中均将冷却水用水冷壁面上的表面对流系数代替。
表6-5 初始仿真模型中各部件的尺寸参数及材料特性(室温)

(2)忽略金刚石生长过程中所有化学反应。化学反应尤其是氢原子在基体表面复合反应会提供大量热量,导致基体温度上升,这是仿真与测温结果出现误差的主要原因。

图6-13 热丝排布参数定义示意
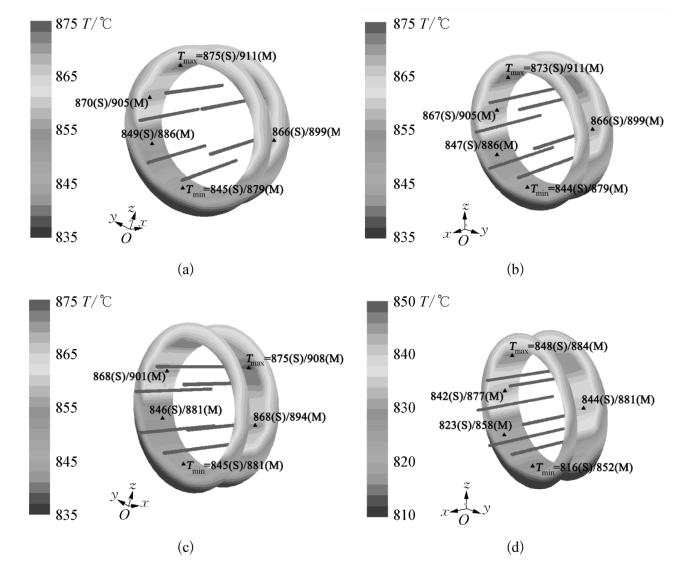
图6-14 不同条件下的温度场分布及对应测温结果
(a)初始模型,纯氢气氛围,表面对流系数55 W/(m2·℃)代替冷却水作用;(b)初始模型,纯氢气氛围,冷却水流量10 mL/s;(c)初始模型,97%氢气+3%丙酮(吸收系数AC=0.2,散射系数SC=0.3);(d)初始模型,40%氢气+60%氩气(AC=0.1,SC=0.2)
(3)氢气是具有典型的对称分子结构的双原子气体,因此将其定义为热辐射透明气体,吸收系数和散射系数均为零。所有固体均定义为辐射不透明体。
(4)金刚石薄膜沉积过程中除氢气外还会采用丙酮、甲烷、甲醇、乙醇等碳源气体以及氩气等惰性气体,这些气体不能视为辐射透明气体。但是在该研究中,由于丙酮的含量很低,并且热传导系数接近氢气,因此其作用被忽略。如图6-14(c)所示为当反应气体定义为97%氢气和3%丙酮(吸收系数AC为0.2,散射系数SC为0.3)的混合气体时的仿真结果,与图6-14(a)的结果基本一致。
(5)在NCD沉积过程中常常会通入大量氩气,氩气的辐射参数对于仿真结果有明显影响,但是没有数据资料可以直接获得氩气的辐射参数,因此本研究中定义反应气体为40%氢气和60%氩气的混合气体,然后采用了多组AC和SC的组合进行仿真,结果发现当两参数分别为0.1和0.2时仿真结果与测温结果比较吻合,如图6-14(d)所示。当沉积NCD时,氩气含量很高,氩气的辐射特性与氢气差异较大,并且氩气的热传导系数也明显小于氢气,因此在仿真时不能忽略其作用。
基于上述论述、验证及模型简化,首先以常规的MCD薄膜沉积为例,深入分析上述热丝参数对于内孔表面温度场分布的具体影响。采用内孔直拉热丝工艺在较小直径(<30 mm)的内孔表面沉积金刚石薄膜时,采用粗细合适、置于内孔轴线上、加热到2 000~2 400℃的单根热丝即可为反应气体分解和加热基体提供足够的能量,并且通过控制热丝温度和热丝直径可以控制基体表面温度在800~900℃的范围内。随着内孔直径的增加,热丝-基体间距增加,一方面热丝辐射难以保证内孔表面的温度达到金刚石薄膜生长所需的数值,另一方面,热丝-基体间距增加,在热丝周围分解生成的活性基团到达基体表面的概率大幅降低,因此热丝根数必须增加且合理排布,方可满足内孔表面金刚石薄膜均匀沉积的要求。用于内孔表面金刚石薄膜均匀沉积的基本的热丝排布方式是以内孔轴线成中心对称的等边多边形热丝排布方式。
在等边多边形热丝排布方式基础上,首先研究了热丝根数N对于内孔表面温度场分布的影响[Tf=2 100℃,df=1 mm,rc=25 mm(单根热丝不适用),h=0,α=变量(单根热丝不适用,N根热丝180°/N,空出零点方向)],结果如图6-15(a)所示,其中温度偏差定义为温差和最小温度的比值,用于评价内孔表面温度场分布的均匀性。随着N的增加,整体辐射热量等比增加,因此内孔表面温度数值急剧上升。不同热丝根数情况下内孔表面温度场分布趋势基本一致,即上方较高下方较低,但是温度偏差会随着N的增加明显减小,说明更多的热丝有助于改善内孔表面温度场分布的均匀性。由于金刚石薄膜沉积过程中热丝温度和基体温度分别需要控制在2 000℃以上以及800~900℃,并且过多热丝在内孔中的协同排布非常困难,因此本研究中将N近似定义为6。
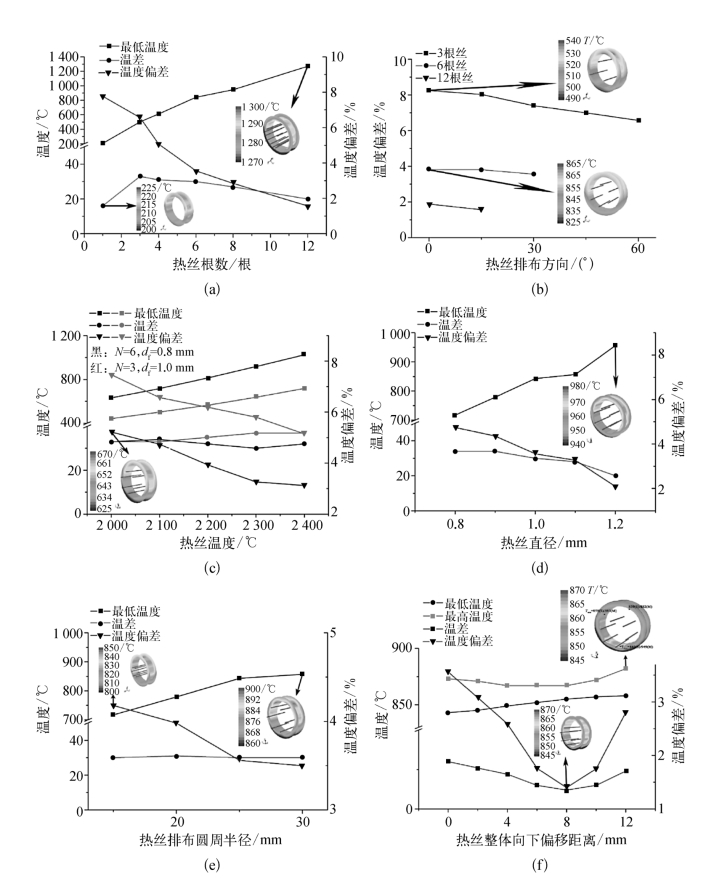
图6-15 热丝排布参数对内孔表面温度场分布的影响
(a)N[Tf=2 100℃,df=1 mm,rc=25 mm(单根不适用),h=0 mm,α可变(单根不适用,N根热丝180°/N)];(b)α(Tf=2 100℃,df=1 mm,rc=25 mm,h=0 mm);(c)Tf(α=180°/N,rc=25 mm,h=0 mm);(d)df(N=6,α=180°/N,Tf=2 100℃,rc=25 mm,h=0 mm);(e)rc(N=6,α=180°/N,Tf=2 100℃,df=1 mm,h=0 mm);(f)h(N=6,α=180°/N,Tf=2 100℃,df=1 mm,rc=25 mm)
在固定的热丝根数情况下,热丝排布的方向α也会显著影响温度分布,相应结果如图6-15(b)所示。当α趋近于0°,即当某根热丝趋近于零点方向时,温度偏差会逐渐增加,这是因为温度最高点原本就位于零点方向,当有一根热丝恰好位于该位置时,温度最高点的温度上升会更加明显。热丝温度Tf和热丝直径df对于内孔表面温度场分布的影响分别如图6-15(c)和(d)所示。随着Tf的升高,内孔表面的温度数值整体上升,但是温差基本保持不变,因此温度偏差略有下降。df的增加可起到类似Tf升高的效果,但是改善内孔表面温度场分布均匀性的效果更明显,温差即随之略有下降,而温度偏差下降更明显,这主要是因为热丝辐射面积增大。
热丝-基体间距不但会影响从热丝到基体的温度梯度,还会影响活性基团到达基体表面的概率,因此对平面或复杂形状外表面金刚石薄膜的沉积都会有显著影响。在内孔区域,虽然热丝-基体间距的调整受到内孔直径的限制,但仍然可以通过采用不同数量的热丝来进行调整,当热丝数量确定后,还可以通过改变热丝排布圆周的半径rc进一步进行调整,其影响规律如图6-15(e)所示,整体温度会随rc的增加略有上升,但是温差基本保持不变,因此温度偏差略有减小。但是如果rc过大,热丝-基体间距很小,靠近基体表面的热丝在金刚石薄膜沉积过程中如果发生抖动,很容易碰触内孔表面。综合以上因素,rc初步确定为20~30 mm。
如前文所述,内孔表面温度分布的基本规律是上方高下方低,因此考虑将所有热丝整体向下平移可能有助于改善温度场分布的均匀性。热丝整体向下偏移的距离h对于内孔表面温度场分布的影响如图6-15(f)所示,最低温度会随着h的增加而增加,但是最高温度、温差和温度偏差都会随着h的增加先降低再升高,当h=8 mm时温度偏差最小。随着h的增加,由于热丝与内孔下方的距离越来越近,因此温度最高点也会逐渐从上方向下方移动。此外,当h增加到12 mm时,内孔下方的仿真结果与测温结果的偏差高达7.5%,而上方的偏差仅有2.6%,实际的温差和温度偏差要比仿真结果更高,这是因为当热丝靠近内孔下方时,热丝周围分解生成的氢原子到达内孔下方表面的概率更高,氢原子复合反应从而可以提供更多的能量。通过测温试验发现,当h大约为5.6 mm时可以获得最小的温差和温度偏差,这说明对h而言,仿真优选的结果与实际优选的结果之间约有30%的偏差,试验数值要采用0.7的补偿系数进行补偿。
2)φ80 mm内孔热丝参数优化及沉积试验
根据前文的讨论结果,针对φ80 mm内孔表面金刚石薄膜沉积过程,α设定为30°,其他参数也可初步限定在合适的范围内。为了进一步优化热丝排布参数,本节中采用L9(34)正交表格安排优化仿真,相应的因素和水平如表6-6所示,因为h还会受到rc的限制,因此表格中的h′定义为11.2-0.288rc。用于优化仿真的L9(34)正交表及相应的仿真分析结果如表6-7所示,其中,Tmin为最低温度,Td为温度偏差,An为对应水平n的平均结果,Rj为极差。所有因素的影响曲线如图6-16所示,Tmin会随四个因素的上升而增加,Td会随Tf、df和rc的上升而减小,当h=2h′mm时Td最小,与前面的讨论结果吻合。在φ80 mm内孔表面沉积MCD的最优热丝排布参数为:Tf=2 200℃,df=0.8 mm,rc=30 mm,h=2h′=2×(11.2-0.288rc)=5.12 mm,对应的温度分布仿真结果如图6-17(a)所示,考虑到仿真与测温试验中对于h值要求的偏差,在测温及实际的金刚石薄膜沉积过程中采用的h=1.4h′=1.4×(11.2-0.288rc)=3.584 mm,如图6-17(a)中所示的测温结果即该情况下得到的结果,与仿真结果具有很好的一致性。
表6-6 用于优化仿真的因素和水平

表6-7 用于优化仿真的L9(34)正交表及相应的仿真分析结果
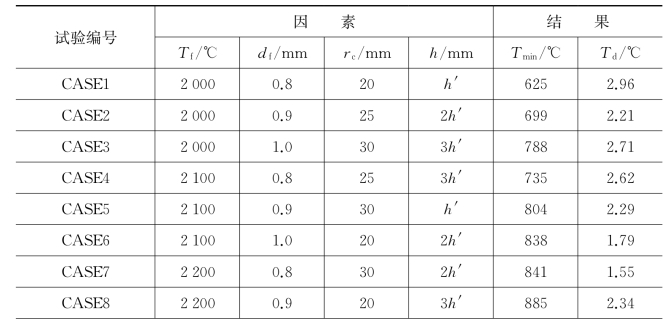
(续表)
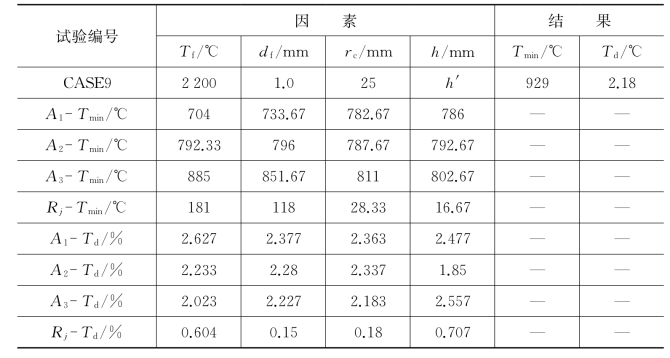
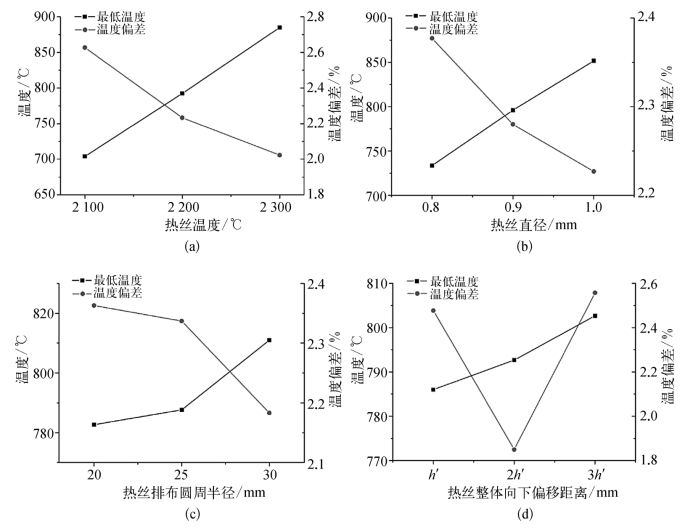
图6-16 (a)Tf、(b)df、(c)rc和(d)h的影响曲线
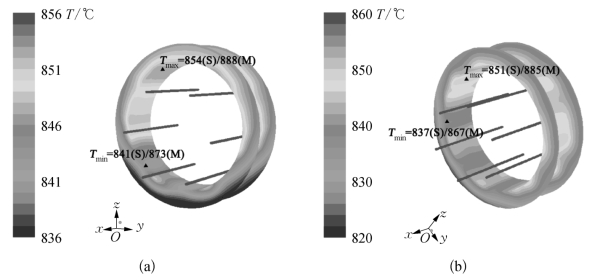
图6-17 用于(a)MCD和(b)NCD薄膜生长的优化热丝排布方案下的仿真及测温结果(https://www.xing528.com)
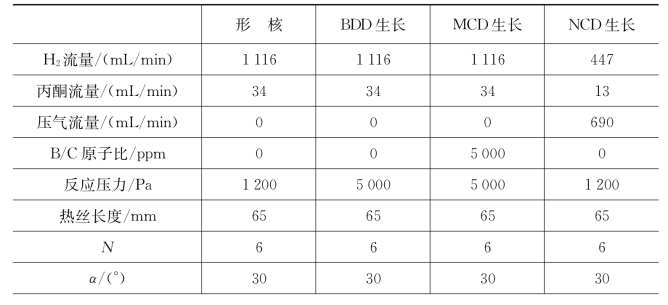
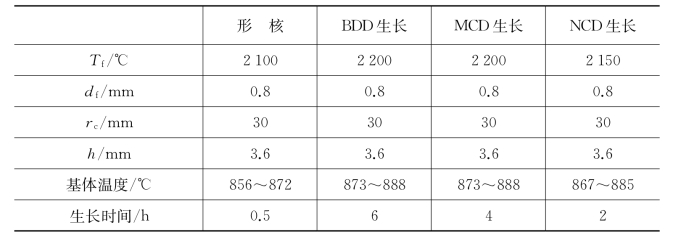
BD-UM-NCCD三层复合金刚石薄膜具有优异的综合性能。因此该薄膜被用作大部分圆孔拉拔模具内孔表面的耐磨涂层。同理,本研究中针对大孔径的SiC紧压模,同样选用该薄膜作为内孔表面保护涂层。BDMCD的生长条件和MCD类似,因此用于其沉积的优化的热丝排布参数同MCD一样。NCD薄膜沉积过程中采用的反应气源是40%的氢气(含丙酮)和60%的氩气,反应压力为1 200 Pa,针对该情况同样对其热丝排布参数进行优化,优化结果如下:Tf=2 150℃,df=0.8 mm,rc=30 mm,h=1.4h′=3.6 mm,对应该情况的仿真及测温结果如图6-17(b)所示。此外,针对形核工况(97%氢气+3%丙酮,反应压力1 200 Pa)的优化结果如下:Tf=2 100℃,df=0.8 mm,rc=30 mm,h=1.4h′=3.6 mm。综上所述,用于BD-UM-NCCD薄膜沉积的具体参数如表6-8所示。
表6-8 φ80 mm内孔表面BD-UM-NCCD薄膜沉积的参数
(续表)
采用如表6-8所述的优化参数在SiC紧压模内孔表面不同位置(温度最高点和温度最低点)沉积的底层BDMCD和BD-UM-NCCD薄膜表面和截面示意图如图6-18(a)和(b)所示,均具有均匀的晶粒尺寸和薄膜厚度。采用初始参数(N=6,α=30°,Tf=2 100℃,df=1 mm,rc=25 mm,h=0 mm)生长6 h的BDMCD薄膜截面形貌如图6-18(c)所示,两个取样点的薄膜厚度存在非常明显的差别,这充分证明了热丝排布参数优化的必要性。图6-18(d)则给出了采用未补偿的热丝排布参数生长6 h的BDMCD薄膜截面形貌,两个取样点的薄膜厚度同样存在明显差别,这证明了对h优化结果进行补偿的必要性和有效性。薄膜拉曼光谱如图6-19所示,薄膜的质量和残余应力也具有较好的均匀性。
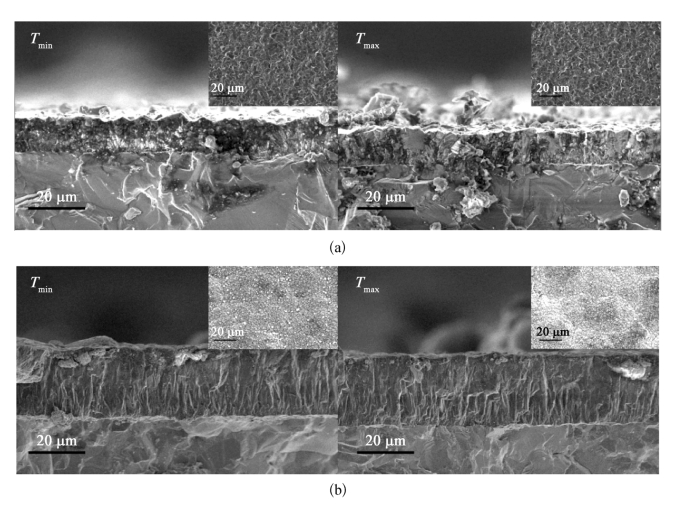
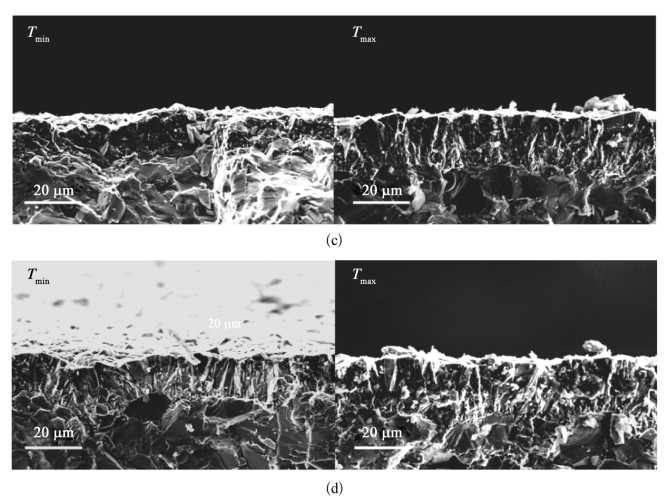
图6-18 采用补偿优化参数在内孔表面温度最高点和最低点沉积的(a)底层BDMCD和(b)BD-UM-NCCD的表面和截面形貌;采用(c)初始参数和(d)未补偿参数(h=5.12 mm)沉积6 h的BDMCD截面形貌
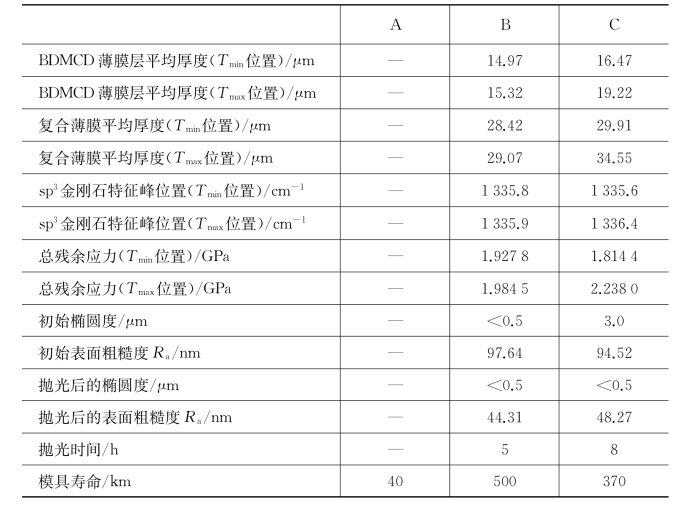
典型模具样品的表征结果及应用性能如表6-9所示,内孔表面薄膜厚度的均匀性会直接影响内孔椭圆度,连同薄膜质量的均匀性会进一步影响抛光的均匀性。抛光过程实质上是对薄膜的一种机械损伤,当内孔椭圆度较高时,抛光同时还要起到整形的作用,因此抛光时间会更长,对于薄膜性能的影响也就更显著。此外,残余应力的均匀性也会影响到金刚石薄膜的使用效果。综上所述,采用补偿优化参数制备的复合金刚石薄膜涂层紧压模的寿命可以达到未涂层模具的12倍,并且要显著长于采用初始参数制备的涂层紧压模寿命。
3)φ50~120 mm内孔热丝排布归一化模型
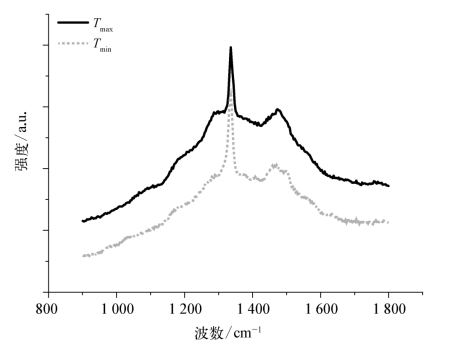
图6-19 采用补偿的最优参数在内孔表面温度最高点和最低点沉积的BD-UM-NCCD薄膜拉曼光谱
表6-9 未涂层SiC紧压模(A)、采用补偿优化参数制备的涂层紧压模(B)及采用初始参数制备的涂层紧压模(C)的表征结果及应用高性能一览表
除SiC材料外,WC-6%Co(质量分数)(YG6/K20)硬质合金材料是更常用的一种模具材料。基于上述热丝排布参数优化方法,我们针对孔径φ50~120 mm的SiC或WC-6%,Co(质量分数)内孔表面金刚石薄膜沉积也进行了相应的热丝排布参数优化、测温及沉积验证试验,部分典型结果如表6-10所示。以这些数据为基础,我们可以归纳出内孔热丝排布的归一化模型。
表6-10 在孔径φ50~120 mm的SiC或WC-6%Co(质量分数)基体内孔表面沉积MCD的优化参数
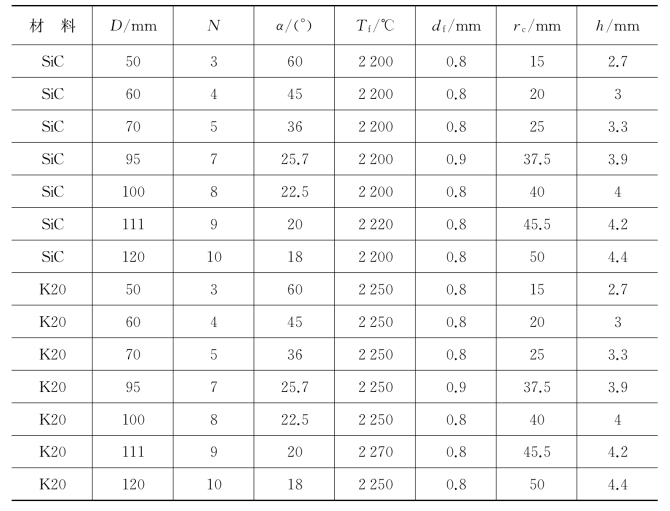
为了保证能够提供充足的能量供应并且获得合适的热丝-基体温度梯度,热丝数量N应该随着基体孔径D的增加而增加。一般来说,对50 mm≤D<60 mm的内孔可采用3根热丝;对60 mm≤D<80 mm的内孔可采用4根或5根热丝;对80 mm≤D<100 mm的内孔可采用6根或7根热丝;对100 mm≤D≤120 mm的内孔可采用8~10根热丝,其规律归纳如下:
![]()
热丝排列角度α会随热丝根数而改变,为了尽量减小内孔上下区域的温差,热丝必须要避开零点方向,因此α可定义为
![]()
热丝温度Tf和热丝直径df是对内孔表面温度数值影响最显著的因素,而二者对于内孔表面温度场分布均匀性的影响相对较小,因此对这两个参数进行调整的主要目的是获得适宜的内孔表面温度。用于确定这两个参数的基本原则是:在一定的D范围内确定热丝数量N,在此基础上df随D的增加而增加;在一定的D范围内确定N和df,Tf可以随D的增加无级增加,具体如下:
![]()
![]()
调整rc的主要目的是调整热丝-基体间距,在前期大量研究中发现,比较合适的热丝-基体间距是10 mm。h的确定需要考虑0.7的补偿系数,因此这两个参数的定义如下:
![]()

上述归一化模型适用于SiC基体内孔表面MCD和BDMCD薄膜的沉积,对于形核阶段(反应气源一样,反应压力1 200 Pa),只需要对热丝温度进行调整即可满足优化要求,热丝温度的定义调整如下:
![]()
对于NCD薄膜的沉积(总反应气体流量一样,包含40%的氢气丙酮和60%的氩气,反应压力1 200 Pa),热丝温度的定义调整如下:
![]()
对于具有较高热传导系数的WC-6%Co(质量分数)基体,热丝温度的定义调整如下:
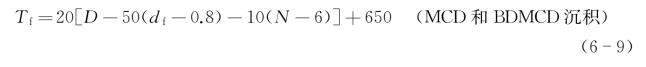
![]()
![]()
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




