无芯头拉管模有限元仿真与优化设计

1）管材无芯头拉拔过程中的缩径缺陷

图5-36　管材无芯头拉拔过程示意

管材无芯头拉拔示意图如图5-36所示，其中模具压缩区与定径区同管材直接接触。传统无芯头拉管模具采用的是锥形压缩区，压缩区的半角α、压缩区与定径区的过渡圆弧半径R以及定径区的长度L成为影响拉拔过程的重要几何参数。在变形过程中，管材与模具压缩区的内壁接触，受压力作用下直径逐渐收缩。管材在无芯头拉拔过程中会产生缩径的质量缺陷。所谓缩径是指无芯头拉拔后的管子外径比其所通过的模孔直径值小的现象。传统的锥形模无芯头拉拔时缩径现象非常普遍，严重的缩径会造成管材的尺寸不合格，导致报废。传统的硬质合金无芯头拉管模具可以通过修模的手段来扩大模具的孔径，减小拉拔产品实际直径同设计要求的差距。而金刚石薄膜一旦涂覆到模具表面，修模会破坏金刚石薄膜涂层，成本太高。因此，需要在沉积金刚石薄膜涂层之前设计好无芯头拉管模具，减小管材的缩径。本节以低碳钢管的拉拔过程为例，研究了金刚石薄膜涂层无芯头拉管模具拉拔过程的有限元仿真及优化设计，金属材料的力学性质在前文中通过拉伸试验得到，金属材料同抛光的金刚石薄膜之间的摩擦系数通过如3.4节所述的标准摩擦磨损试验测量而得。管材的初始直径为14.00 mm，壁厚2.00 mm，拉管模具的内孔直径为12.60 mm。

为了解释缩径现象产生的机理，本节采用有限元仿真分析的方法对管材无芯头拉拔过程进行模拟，以便直观的观测金属管材在变形过程中的流动规律。如图5-37所示为压缩区半角α为12°、过渡圆弧R为3 mm、定径区长度L为3 mm时，低碳钢管材无芯头拉拔的有限元模拟结果。从图5-37（a）中可以看出，当管材进入定径区之后，塑形应变仍然继续增大，这说明管材仍然发生塑形变形。同样的结论可以从金属流动的速度的规律中可以得到，如图5-37（b）所示，随着管材进入压缩区，模具的截面面积逐渐缩小，管材流动的速度逐渐增大。而其沿径向方向的分量也随之增大，在压缩区的末端时达到最大值，如图5-37（c）所示。当管材进入定径区之后，金属流动速度沿径向方向的分量无法立刻降为0，管材还会继续收缩一段距离，由此产生了缩径现象。最终管材的直径为12.331 mm。通常金属管材产品允许的公差带为±0.02 mm，由当前设计的无芯头拉管模具生产出来的低碳钢管尺寸超出了公差带的范围，属于不合格产品。

图5-37　使用传统拉拔模具进行低碳钢管无芯头拉拔有限元结果

（a）塑形应变；（b）金属流动速度；（c）金属流动速度沿径向的分量

为了对比不同设计参数无芯头拉管模具的缩径情况，改变锥形无芯头拉管模具的设计参数（压缩区半角α、压缩区与定径区的过渡圆弧R以及定径区长度L）进行有限元仿真分析，实验方案如表5-16所示。图5-38给出了仿真结果同公差带的比较，从图中可知传统的锥形无芯头拉管模具的缩径现象十分严重，难以作为金刚石薄膜涂层无芯头拉管模具的设计。

图5-38　使用传统锥形无芯头拉管模具拉拔生产的管材直径同公差带的比较

表5-16　使用不同设计参数的锥形无芯头拉管模具拉拔所得的管材直径

（续表）

2）改进型无芯头拉管模具

为了解决金属管材无芯头拉拔过程当中的缩径问题，本节提出一种改进型的无芯头拉管模具设计，如图5-39所示为其示意图。相比传统的锥形无芯头拉管模具，改进型的无芯头拉管模具的压缩区由两个锥面组成。通过增加一个次压缩区，改善了金属管材在压缩区的流动情况。改进型的无芯头拉管模具的主要设计参数包括定径区长度L1、模具主压缩区半角α1、次压缩区半角α2及次压缩区的长度L2，比传统的锥形无芯头拉管模具多一个设计变量，通过优化模具的几何参数，达到减小缩径的目的。

图5-39　改进型无芯头拉管模具示意

本节对改进型无芯头拉管模具的拉拔过程进行了有限元仿真分析，以研究应用改进型无芯头拉管模具时金属管材流动的情况。初始的设计参数定径区长度L设定为3 mm，主压缩区半角α1为12°，次压缩区半角α2为5°，次压缩区长度L2为4 mm。仿真结果如图5-40所示。从图5-40（a）中可以看出，当管材进入定径区后，塑形应变基本就稳定下来，不再增长。同使用锥形无芯头拉管模具时一样，随着管材进入压缩区，模具的截面面积逐渐缩小，管材流动的速度逐渐增大。而金属流动速度沿径向分量的变化情况则有所不同。如图5-40（c）所示，当管材达到主压缩区的末端时，金属流动速度沿径向的分量达到最大值；但当管材进入次压缩区时，虽然金属流动的速度仍然增大，但由于金属流动的方向发生改变，因此其沿径向分量反而逐渐减小。当管材进入定径区时，其值降到很小，管材收缩的量大幅减少。使用当前设计参数的改进型无芯头拉管模具仿真计算所得的管材直径为12.558 mm。由此可见改进型无芯头拉管模具设计能够大幅度改善金属管材无芯头拉拔过程中的缩径现象。

图5-40　使用改进型无芯头拉管模具的低碳钢管无芯头拉拔有限元结果

（a）塑形应变；（b）金属流动速度；（c）金属流动速度沿径向的分量

3）改进型模具无芯头拉拔有限元仿真结果分析

如图5-41（a）所示为低碳钢管无芯头拉拔过程中管材的轴向应力分布云图。测量管材上距离内壁不同位置上的点，得到轴向应力随时间变化的曲线如图5-41（b）所示（T为管材壁厚，t为观测点所在位置距内壁的距离，t/T从0到1表示了从轴心到外表不同的点）。在无芯头拉拔过程中，管材的内表面处于自由运动的状态，而外表面与模具接触，由于摩擦力的作用，使得管材的外表面比内表面承受了更大的流动阻力，造成管材断面上金属流动的不均匀。从应力分析的结果中可以看出，管材在无芯头拉拔过程中的轴向应力大致经历了三个变化的过程。在进入压缩区之前，管材由于受到前方收缩的金属的作用，管材发生向内的弯曲，使得管材的外表面产生轴向拉应力，而内表面产生轴向压应力。在进入压缩区之后，管材外表面与模具内孔发生接触，由于模具压缩区的挤压作用，使管材的轴向应力产生与进入压缩区之前完全相反的应力模式，外表面为轴向压应力，内表面为轴向拉应力。管材进入定径区之后，发生向外的弯曲，变形过程与定径区内的变形相反，其外表面产生较大的拉应力，内表面产生较大的压应力。如果管材轴向的拉应力过大，管材表面容易产生横向的裂纹，影响产品的质量，严重时甚至会造成管材的断裂，不仅浪费金属材料，而且极大地降低了管材生产的效率。

图5-41　低碳钢管无芯头拉拔过程中的轴向应力

（a）低碳钢管无芯头拉拔过程中的轴向应力云图；（b）低碳钢管无芯头拉拔过程中管材上不同位置的轴向应力随时间变化的比较

如图5-42（a）所示为低碳钢管无芯头拉拔过程中的径向应力云图，测量管材上距离内表面不同位置上的点，即可得到径向应力随时间变化的曲线，如图5-42（b）所示。由于受到模具压缩区的挤压，管材处于压应力的状态。进入定径区之后，管材的内表面和外表面的应力值比较小，而管材中心部位处于压应力状态，径向应力在管材截面上的分布是不均匀的。

图5-42　低碳钢管无芯头拉拔过程中的径向应力

（a）低碳钢管无芯头拉拔过程中的径向应力云图；（b）低碳钢管无芯头拉拔过程中管材上不同位置的径向应力随时间变化的比较

图5-43　低碳钢管无芯头拉拔过程中的环向应力

（a）低碳钢管无芯头拉拔过程中的环向应力云图；（b）低碳钢管无芯头拉拔过程中管材上不同位置的环向应力随时间变化的比较

如图5-43（a）所示为低碳钢管无芯头拉拔过程中的管材的环向应力云图。测量管材上距离内表面不同距离的点，即可得到环向应力随时间变化的曲线，如图5-43（b）所示。在管材与模具压缩区接触之后，由于受到压缩区的挤压，管材处于压应力的状态，外表面的压应力值最大。进入定径区之后，管材在金属弹性回复的作用下，环向应力沿着直径方向出现不均匀的分布，最大的压应力值出现在管材的外表面，内部呈现压应力值状态，中心位置的压应力值最大。当定径区管材外表面的环向应力过大时，管材外表面容易产生纵向的裂纹，影响产品的质量。

如图5-44所示为金刚石薄膜涂层无芯头拉管模具在低碳钢管无芯头拉拔过程中所产生的von-Mise等效应力分布云图，从图中可以观察到，在管材和模具开始接触的地方和压缩区的末端出现了应力集中的现象。如果这两处的应力值过大，会引起金刚石薄膜涂层剥落，导致金刚石薄膜涂层拉丝模具失效，缩短工作寿命。

图5-44　低碳钢管无芯头拉拔过程中模具上的von-Mises等效应力

4）无芯头拉管模具优化设计

改进型金刚石薄膜涂层无芯头拉管模具需要设计的几何参数主要包括定径区长度L1、模具主压缩区半角α1、次压缩区半角α2及次压缩区的长度L2。在实际生产当中，如何正确地选择金刚石薄膜涂层无芯头拉管模具的几何参数对于提高无芯头拉拔生产管材的产品质量和生产效率、减小残余应力以及延长模具工作寿命具有十分重要的作用。因此，有必要研究金刚石薄膜涂层无芯头拉管模具的几何参数对金属管材的拉拔过程的影响规律，以提高管材产品的质量和拉拔过程的生产效率。本节采用有限元仿真的方法研究了金刚石薄膜涂层无芯头拉管模具几何参数对金属管材无芯头拉拔过程的影响规律，并采用响应面法对无芯头拉管模具的几何参数进行了优化设计［128］。

为了获得最有的管材无芯头拉管模具的几何参数，以改进型无芯头拉管模具的定径区长度L1、模具主压缩区半角α1、次压缩区半角α2及次压缩区的长度L2作为设计变量。结合实际生产经验，各个变量的具体取值范围见表5-17。

表5-17　设计变量及其取值范围

管材无芯头拉拔过程中的缩径缺陷十分普遍，严重的缩径会导致产品不合格而报废。因此，将拉拔后的产品管径作为优化问题的约束条件。然后，本节以无芯头拉拔过程中管材表面的轴向应力、模具上的von-Mises等效应力以及拉拔力作为优化问题所需要进行优化的目标。通常，管材表面轴向应力过大会导致横向裂纹的产生，而较大的von-Mises等效应力会导致模具的磨损加剧，造成模具寿命的减短，因此优化设计的目标是这两个应力值越小越好。在管材无芯头拉拔生产过程当中，过大的拉拔力会导致管材断裂，严重影响生产效率，浪费原材料，因此拉拔力也应该越小越好。

基于Box-Behnken实验设计方法，针对所选的四个设计变量进行搭配组合，共29组实验方案，相应的设计数据如表5-18所示。对于得到的每一组实验方案，重新构建几何模型，利用有限元软件ANSYS Workbench进行数值计算，得到相应的产品直径D、线材轴向应力S1、模具von-Mises等效应力S2及拉拔力F，模拟结果如表5-19所示。

表5-18　根据Box-Behnken中心组合设计确定实验点

表5-19　有限元仿真结果(www.xing528.com)

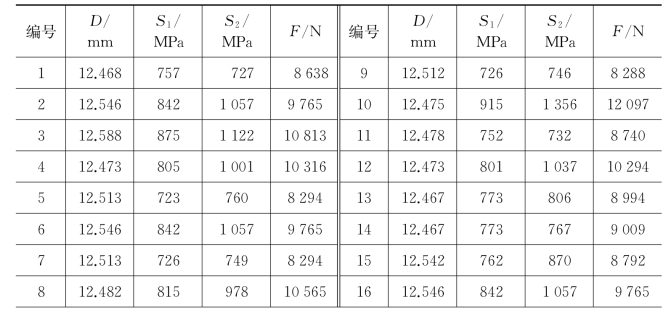
（续表）

根据表5-19中的数据，利用最小二乘法拟合响应面，得到管材无芯头拉拔时产品直径D、轴向应力S1、模具von-Mises等效应力S2及拉拔力F与拉拔模具各设计变量的响应模型如下：

以上四个响应面模型可以用来预测不同设计变量下的无芯头拉拔管材产品直径D、轴向应力S1、模具von-Mises等效应力S2及拉拔力F。图5-45（a）、（b）、（c）和（d）分别是不同响应通过响应面模型的预测值和有限元模拟的实际值的对比，可以看出，预测值和模拟结果基本一致，说明回归模型的预测结果较为准确。

图5-45　预测值和实际值对比

（a）管材直径；（b）管材轴向应力；（c）模具应力；（d）拉拔力

为了进一步定量地分析各个设计变量对模拟结果的影响以及评价实验结果的可靠性及数学模型的可信度，需要对模拟的结果进行方差分析。如表5-20所示为低碳钢管直径的方差分析结果，模型的校正系数为0.931 2，说明模型能够解释93.12%的响应值变化，仅有6.88%的变异不能通过此模型来解释。相关系数为0.965 6，说明模型的拟合程度良好，误差较小。模型的信噪比为18.806，大于4，说明模型具有足够的分辨能力。从表5-20中可以看出其中C、D、CD及D2是低碳钢丝直径响应模型的显著项。

表5-20　低碳钢管直径的方差分析

如表5-21所示为低碳钢管轴向应力响应模型的方差分析结果。由表可知，模型的拟合程度良好，误差较小。模型中B、C、D和D2是管材轴向应力响应模型的显著项。如表5-22所示为模具应力响应模型的方差分析结果。由表可知，模型的拟合程度良好，误差较小。模型中B、C、D、BC、BD、CD和D2是模具应力响应模型的显著项。如表5-23所示为拉拔力的响应模型的方差分析结果。由表可知，模型的拟合程度良好，误差较小。模型中B、C、D、BC、BD、CD和D2是拉拔力响应模型的显著项。

表5-21　低碳钢管轴向应力的方差分析

（续表）

表5-22　模具应力的方差分析

表5-23　拉拔力的方差分析

本节借助二阶响应面研究了无芯头拉管模具的几何参数对优化目标的影响。图5-46（a）和（b）给出了L1＝4 mm、α1＝14°时，α2和L2对低碳钢管直径的交互作用的响应面及等高线图。从图中可知随着次压缩区半角的增大，低碳钢管的直径逐渐减小；当次压缩区半角固定时，管材直径随次压缩区长度的变化存在极大值；而当次压缩区半角比较小时，管材直径随次压缩区长度变化的幅度比较大。

图5-46　不同设计变量对低碳钢管直径的影响

（a）次压缩区半角和次压缩区长度的交互作用响应面；（b）次压缩区半角和次压缩区长度的交互作用等高线

图5-47给出了α1、α2和L2对低碳钢管轴向应力的影响。从图中可以看出，管材的轴向应力随着主压缩区半角的增大而增大，随着次压缩区半角的增大而减小。当其他设计变量固定不变时，管材轴向应力随着次压缩区长度变化存在极大值。

图5-47　不同设计变量对低碳钢管轴向应力的影响

（a）主压缩区半角；（b）次压缩区半角；（c）次压缩区长度

图5-48给出了α1、α2和L2及其之间的交互作用对模具应力的影响。图5-48（a）和（b）给出了α1和α2对模具应力的交互作用的响应面及等高线。从图中可以看出轴向应力随着主压缩区半角的增大而增大，随着压缩区半角的增大而减小。当主压缩区半角较大时，轴向应力随次压缩区半角变化的幅度较大；当次压缩区半角较小时，轴向应力随主压缩区半角变化的幅度较大。图5-48（c）和（d）给出了α1和L2对模具应力的交互作用的响应面及等高线。从图中可以看出轴向应力随着压缩区长度的增大而减小；当主压缩区半角较大时，轴向应力随次压缩区长度变化的幅度较大；当次压缩区长度较小时，轴向应力随主压缩区半角变化的幅度较大。图5-48（e）和（f）给出了α2和L2对模具应力的交互作用的响应面及等高线。从图中可以看出当次压缩区半角较大时，轴向应力随次压缩区长度变化的幅度较大；当次压缩区长度较大时，轴向应力随次压缩区半角变化的幅度较大。

图5-48　不同设计变量对模具应力的影响

（a）主压缩区半角和次压缩区半角的交互作用响应面；（b）主压缩区半角和次压缩区半角的交互作用等高线；（c）主压缩区半角和次压缩区长度的交互作用响应面；（d）主压缩区半角和次压缩区长度的交互作用等高线；（e）次压缩区半角和次压缩区长度的交互作用响应面；（f）次压缩区半角和次压缩区长度的交互作用等高线

如图5-49所示为α1、α2和L2及其之间的交互作用对拉拔力的影响。拉拔力随着主压缩区半角的增大而增大，随着压缩区半角的增大而减小。当主压缩区半角较大时，拉拔力随次压缩区半角变化的幅度较大；当次压缩区半角较小时，拉拔力随主压缩区半角变化的幅度较大。拉拔力随着压缩区长度的增大而减小。当主压缩区半角较大时，拉拔力随次压缩区长度变化的幅度较大；当次压缩区长度较小时，拉拔力随主压缩区半角变化的幅度较大。当次压缩区半角较大时，拉拔力随次压缩区长度变化的幅度较大；当次压缩区长度较大时，拉拔力随次压缩区半角变化的幅度较大。

图5-49　不同设计变量对拉拔力的影响

（a）主压缩区半角和次压缩区半角的交互作用响应面；（b）主压缩区半角和次压缩区半角的交互作用等高线；（c）主压缩区半角和次压缩区长度的交互作用响应面；（d）主压缩区半角和次压缩区长度的交互作用等高线；（e）次压缩区半角和次压缩区长度的交互作用响应面；（f）次压缩区半角和次压缩区长度的交互作用等高线

通过以上分析，可以看出无芯头拉管模具几何参数对管材的直径、轴向应力、模具应力及拉拔力的影响十分显著。为了保证管材产品的尺寸和质量，提高模具寿命，减小拉拔力，本节以管材直径落在公差带范围内（±0.02 mm）为约束条件，以管材轴向应力、模具应力和拉拔力的综合影响最小为优化目标，使用满意度函数法将多目标优化问题转化为单一目标优化问题，对无芯头拉管模具的几何参数进行优化。整个优化问题可以通过以下数学模型进行描述：

Find：L1，α1，α2，L2

Minimize：f（S1（L1，α1，α2，L2），S2（L1，α1，α2，L2），F（L1，α1，α2，L2））

Subject to constraints：12.58 mm≤D（L1，α1，α2，L2）≤12.62 mm

Within ranges：2 mm≤L1≤5 mm，10°≤α1≤18°，4°≤α2≤8°，1 mm≤L2≤5 mm

根据满意度函数法，利用之前所建立的各个优化目标与设计变量之间的响应模型，得到最优的低碳钢管金刚石薄膜涂层无芯头拉管模具的几何参数。对得到的优化参数进行进一步的有限元模拟分析，优化参数和模拟结果如表5-24所示。

表5-24　优化参数及其有限元模拟结果