基于响应面法的多目标优化设计方法

1）试验设计

要确定设计参数对拉拔过程的影响，必须进行试验设计，使得计算的结果适用于科学分析，从而得出有效和客观的结论。CVD金刚石薄膜涂层拉拔模具需要设计的几何参数主要包括压缩区工作半角α、过渡圆弧R和定径区长度L。可以进行响应面分析的试验设计方法有很多种，其中最常用的为中心复合设计和响应面优化分析。

中心复合设计（central composite design，CCD）也称为星点设计。图5-4（a）给出了其样本采集点的分布。通常来讲，CCD是由2k的析因设计、2k个坐标试验点和一定数量的中心试验点组成，试验设计安排表见表5-2。

表5-2　CCD和BBD 试验次数比较

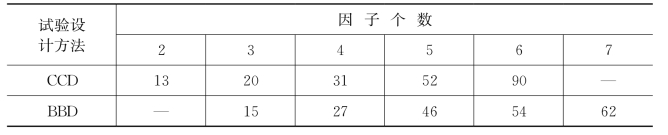
响应面优化分析（Box-Behnken design，BBD）也是响应面优化法常用的试验设计方法，其样本采集点如图5-4（b）所示。在相同因子数条件下，一般BBD试验设计比CCD试验设计的试验点数目少，如表5-2所示，效率更高，且所有的影响因素不会同时处于高水平。本书采用BBD试验设计方法选取采样点。

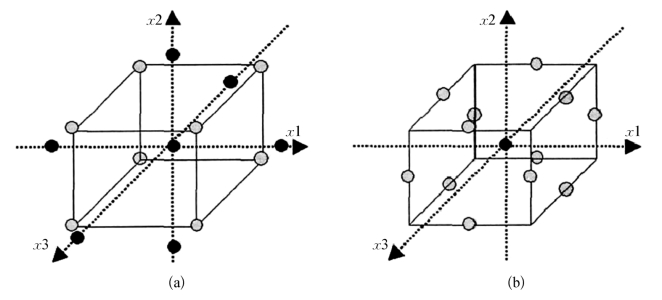
图5-4　CCD和BBD的样本采集点

（a）CCD；（b）BBD

2）响应面法

响应面法（response surface methodology，RSM）是数学方法和统计方法相结合，针对多个变量和响应的分析方法，通过近似的思想、实验设计及拟合等手段对工程问题进行优化设计。模具几何参数优化中，目标函数与设计变量之间的关系通常很难用精确的数学函数来表达。因此，采用响应面法近似表达变量与目标之间的关系，非常适用于金刚石薄膜涂层拉拔模具的优化设计。

响应面法可用来对响应受到多个变量影响的问题进行建模和分析，其目的是优化该响应。按照统计学术语，设计变量为以因子，设计目标和约束称为响应。响应面是指响应y与一组输入之间存在函数关系式

由式（5-6）所表示的曲面称为响应面。广泛采用响应和一组因子x相关的低阶多项式作为响应面近似函数。本书选择二阶响应曲面模型来预测不同设计变量组合下的响应值，其表达式为

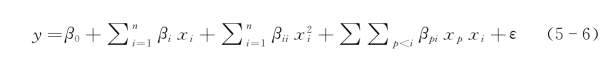
式中，xi为设计变量；ε为残余误差；β0、βi、βii、βpi均为待定系数。

可将上式转换成多元线性回归模型，即

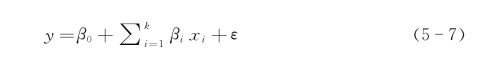
为了估计参数β0，β1，…，βk，采用最小二乘法，设b0，b1，…，bk分别是参数β0，β1，…，βk的最小二乘估计，则回归方程为

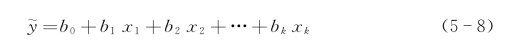
由最小二乘法可知，b0，b1，…，bk应使全部观测值yi与回归值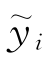之间的偏差平方和Q达到最小，即(www.xing528.com)

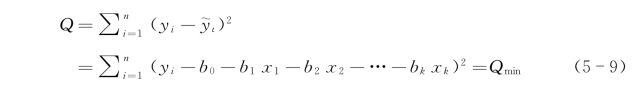
根据微积分学的极值定理知b0，b1，…，bk应是下列方程组的解

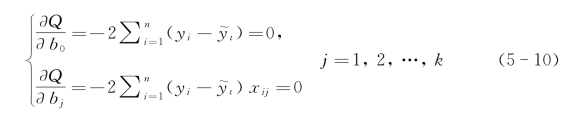
解以上方程组可得系数向量β的无偏差估计为

3）满意度函数法多目标优化

金刚石薄膜涂层拉拔模具优化设计问题是一个多目标优化问题，通常多个目标之间是相互矛盾的，因此需要权衡多个目标并得到折中最优解。为解决这一多目标问题，本书采用的方法是使用满意度函数法将多目标优化问题转化为单一目标的优化问题。

满意度函数法是一种简便易行、应用广泛的多目标优化的方法。其总体思想是将所有的优化目标的值转化为0到1之间的数，即d（Yi）（i＝1，2，…，q），且d（Yi）随着优化目标的满意度增大而增大，将这些d（Yi）的几何平均定义为多目标优化问题的总体满意度函数，从而可实现从多目标优化问题转化为单目标优化问题。

对于望大特征的响应，其满意度函数为

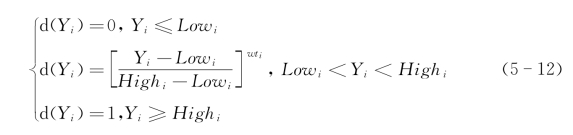
对于望小特征的响应，其满意度函数为

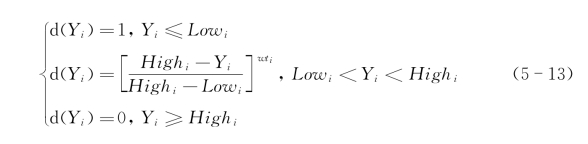
对于望目特征的响应，其满意度函数为

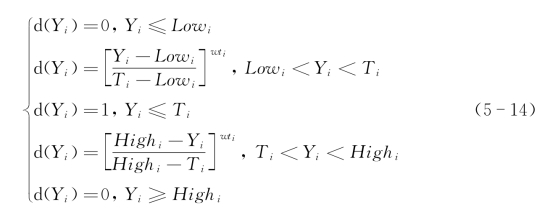
式中，Yi为第i个响应的预测值，Lowi为响应i的下限，Highi为响应i的上限，ti为响应i的目标值，wti为常数，决定满意度函数的形状。图5-5展示了不同常数下的满意度函数曲线。

多目标优化问题的总满意度函数为

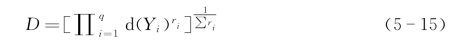
式中，ri为响应i的权重，，q为响应个数。

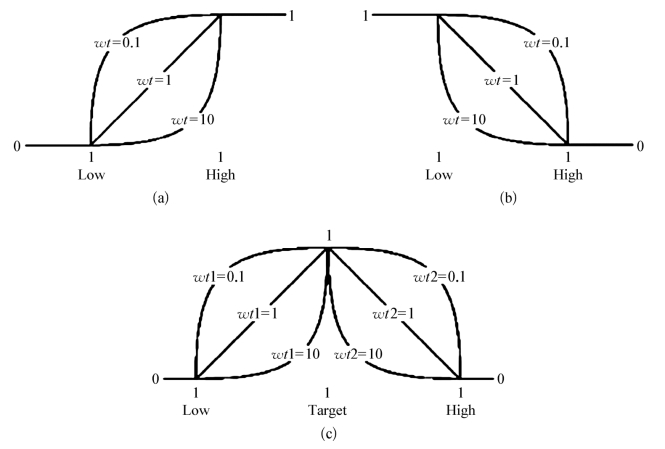
图5-5　满意度函数

（a）望大特征；（b）望小特征；（c）望目特征