主坝有限元分析优化方案

上水库主坝最大坝高94.80m，属1级建筑物，地震设计烈度8度，按《混凝土面板堆石坝设计规范》（DL/T 5016—1999）中11.2.1条和11.2.3条规定，针对坝体的静力和动力应力应变、材料参数敏感性、局部地质明显变化段进行有限元分析计算。

有限元计算采用清华大学岩土工程研究所TOSS3D土石坝应力应变分析程序，TOSS3D包含有线弹性、黏弹性、非线性弹性、弹塑性模型等多种岩土材料本构模型以及理想弹塑性、Clough Duncan非线性弹性、弹塑性损伤模型等多种土与结构接触面本构模型。

坝体堆石料的静动力学特性及计算模型参数利用室内大型高压多功能静动三轴试验机进行静动力三轴等项试验获得，在此基础上，模拟坝体施工过程和蓄水过程，进行坝体的二维、三维静动力非线性有限元应力变形分析。

4.1.5.1　主坝有限元计算参数试验成果分析

试验主要通过坝料静动三轴试验分析模型计算参数，主要包括如下内容：

（1）对上水库主坝的主要坝料和坝基覆盖层材料进行了大型或中型静力三轴试验，测定了其应力-应变-体变关系，进行试验的土石料包括：坝体主堆石料、次堆石料、过渡料、垫层料、排水带料、河床覆盖层料、左岸覆盖层料1（含石量80%）、左岸覆盖层料2（含石量40%）共8种材料。

（2）强度及模型计算参数：根据上述大型常规三轴试验成果，分别求取了各种材料的强度参数、邓肯张EB非线性弹性模型计算参数、沈珠江双屈服面弹塑性模型计算参数和清华非线性解耦KG模型计算参数，为坝体的有限元稳定和应力变形计算分析提供依据。

（3）动剪切模量与动阻尼比试验：对坝体主堆石料、次堆石料、过渡料、垫层料、河床覆盖层料和排水带料共六种材料，通过一系列动三轴试验测定其动剪切模量和动阻尼比，并求取计算用模型参数。

（4）动残余变形试验：对坝体主堆石料、次堆石料、过渡料、垫层料、河床覆盖层料和排水带料共6种材料，通过一系列动三轴试验测定其动残余变形，并求取计算用模型参数。

试验于2005年初进行，当时大坝填筑高程在710.00m左右，试验土料由施工现场开采运至北京实验室，可以反映施工真实状况下坝体应力应变。

1.强度及模型静力计算参数

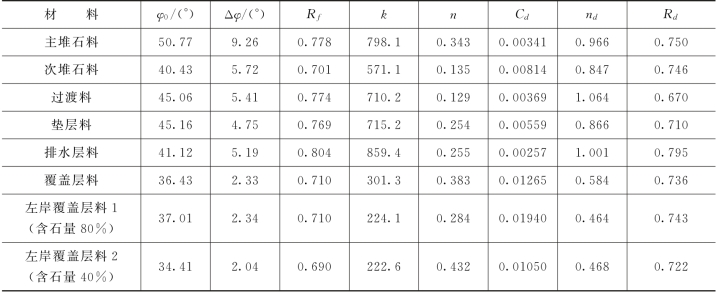
根据常规三轴试验结果整理得到材料的抗剪强度参数，对堆石体常采用非线性强度指标，黏聚力c取为0，试验成果见表4.1-16。

表4.1-16　各种材料的强度参数

邓肯张EB模型属于非线性弹性模型，φ0、Δφ、Rf、k、n、kb、m和kur八个模型参数可由常规三轴试验确定，一般取kur=（1.5～2.0）k，试验得到的各种土料的邓肯张EB模型计算参数见表4.1-17。

沈珠江双屈服面模型属于弹塑性模型，采用体积屈服面和剪切屈服面两个屈服面来描述土体的屈服特性，模型共有φ0、Δφ、Rf、k、n、cd、nd、Rd和Eur 9个模型参数，由一组常规三轴压缩试验结果确定，除cd、nd和Rd外，其余参数均同邓肯张模型共用，计算参数见表4.1-18。

表4.1-17　邓肯张EB模型计算参数表

表4.1-18　沈珠江双屈服面弹塑性模型计算参数表

清华非线性解耦KG模型研究了变形参数的增量回归方法，计算参数见表4.1-19。

表4.1-19　清华非线性解耦KG模型计算参数表

2.动剪切模量与动阻尼比试验成果

通过对主堆石料、次堆石料、过渡料、垫层料、河床覆盖层料和排水带料6种材料的系列动三轴试验测定其动剪切模量和动阻尼比，求取模型参数见表4.1-20。

表4.1-20　各种材料动剪模量和阻尼比参数

3.动残余变形试验成果

通过对主堆石料、次堆石料、过渡料、垫层料、河床覆盖层料和排水带料6种材料的系列动三轴试验测定其动残余变形，求取模型参数见表4.1-21。

表4.1-21　各种材料动残余变形参数

4.1.5.2　主坝静力应力应变分析与安全评价

在主坝有限元计算参数试验成果分析的基础上，土石料分别采用邓肯张EB模型、沈珠江双屈服面模型、清华非线性解耦KG模型，面板沥青混凝土材料分别采用弹性模型和黏弹性模型，模拟坝体的施工和水库的蓄水过程，对坝体进行了静力非线性有限元应力变形分析，研究上水库主坝堆石体及面板的应力和变形特性，对工程的安全性进行评价。

1.二维计算剖面与计算网格

坝体二维计算分析选取坝体的最大剖面坝0+326.50（B17-B17剖面）作为典型断面进行计算分析，为比较分析考虑不同范围的坝后堆渣对大坝及其上游面板应力和变形分布的影响，并为坝体三维计算分析中计算断面的选取提供依据，对所选取的坝体最大剖面（B17-B17剖面）分别采用了三种计算范围，下文中分别简称为方案Ⅰ、方案Ⅱ和方案Ⅲ。在上述的3个剖面中，坝体部分完全相同，主要区别为它们所考虑的坝后堆渣的范围不同，其中方案Ⅰ考虑了下游堆渣区的全部；方案Ⅱ考虑了下游部分堆渣区的影响（具体取高程768m堆渣平台宽度20m，下游坡1∶2.5）；方案Ⅲ只考虑了下游碾压堆渣区的影响。

单元以4结点四边形单元为主，辅以少数三角形过渡单元。其中，方案Ⅰ对应的计算网格共包括单元总数566，结点总数604；方案Ⅱ对应的计算网格共包括单元总数517，结点总数553；方案Ⅲ对应的计算网格共包括单元总数488，结点总数523。

2.三维计算剖面与计算网格

上库主坝整体具有一反拱形式的坝轴线，为反映坝体空间特殊形状的影响，在三维计算中，除了坝体的主体部分之外，还选取坝体两端库岸面板段和坝前库底的一部分作为计算区域，三维有限元计算分析采用考虑了部分下游堆渣区影响（具体取768m堆渣平台宽度20m，下游坡1∶2.5）的计算分析区域，该有限元计算网格共包含结点总数11183，单元总数10879，沿坝轴线（圆弧状）方向的计算断面共分30个断面。

3.左岸冲沟影响的三维计算

选取左岸典型坝段采用三维静力有限元法，计算分析了左岸坝段岸坡基础冲沟对坝体尤其是沥青混凝土面板应力和应变性状的影响，计算的区域选取左岸0+000.00～0+070.00，三维计算网格共包括4567个结点，4078个单元。

4.右岸面板连接处的二维计算分析

选取右岸弧形面板和直线形面板连接处的两个典型剖面，进行了二维有限元计算分析，研究了连接过渡段由于混凝土导墙以及廊道处面板下部压缩覆盖层厚度的突变所致的不均匀变形对面板应力和应变性状的影响。

5.施工顺序与计算分级

有限元计算根据坝体填筑过程和水库蓄水过程共分5级：

（1）地基覆盖层。

（2）上游坝脚线与下游坝脚线以内范围坝体堆石填筑，上游库底填渣、下游堆渣的填筑随主坝同步上升。主堆料、垫层料和过渡料平起作业，整个坝体填筑均衡上升，计算中上述坝体的填筑过程又分为多个荷载分级进行模拟；另外，对于全部考虑下游堆渣的计算方案，为了模拟堆渣的先期填筑过程，还增加了若干个针对下游堆渣的荷载分级。

（3）沥青混凝土面板施工。

（4）库区黏土铺盖层的填筑。

（5）水库的蓄水过程：初步蓄水至758.00m，5个月完成；后期蓄水758.00～789.60m，初步考虑按3.0m/d的平均加载，每3m隔2天，1个月完成。

对所有的计算方案，均考虑和模拟了上述坝体填筑和水库蓄水过程。

6.静力计算模型参数

在非线性有限元计算基本分析方案中，沥青混凝土面板采用线弹性模型，坝基覆盖层料和各种坝体堆石料均采用邓肯张EB非线性弹性模型来描述。为研究本构模型对计算结果的影响，还采用沈珠江双屈服面模型进行了二维和三维计算。

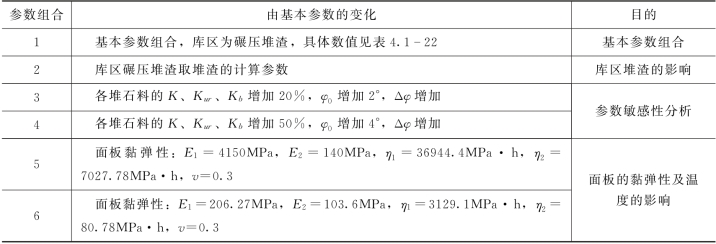
各种材料邓肯张EB和双屈服面本构模型的基本计算参数组合见表4.1-22。

表4.1-22　材料计算参数-第1组（基本参数组合）

注 覆盖层料2为左岸坝基覆盖层料，含石量取40%。

考虑坝料的变异性，对坝料的变形参数进行了敏感性计算分析，表4.1-23列出了参数敏感性分析所采用的几组参数组合。

表4.1-23　静力计算其他参数组合

7.静力计算方案

计算方案编号由计算维数、本构模型名称、计算的材料参数组合和下游堆渣考虑范围或计算剖面复合而成。静力计算的各种方案汇总于表4.1-24。

表4.1-24　静力计算方案及计算内容一览

续表

注 剖面k k对应桩号为坝0+568.38，剖面d d为坝0+600.37断面处沿廊道向剖面。

方案编号的具体形式为：

P+“-计算维数”+“-本构模型名称”+“-材料参数组合号”+“-下游堆渣考虑范围或计算剖面”。其中：

（1）P：“Plan”的简写，代表方案。

（2）计算维数：为“2D”和“3D”，分别代表二维和三维有限元计算。

（3）本构模型名称：为“EB”、“SH”或“VE”，代表计算中堆石料和沥青混凝土面板所使用的本构模型，“EB”表示堆石料采用邓肯-张EB模型，沥青混凝土面板使用弹性模型；“SH”表示堆石料采用沈珠江双屈服面模型，沥青混凝土面板使用弹性模型；“VE”代表表示堆石料采用邓肯张EB模型，沥青混凝土面板使用黏弹性模型。

（4）材料参数组合号：计算中使用的材料参数的组合，具体见表4.1-22和表4.1-23。

（5）下游堆渣考虑范围或计算剖面：对下游堆渣的考虑范围分别为“Ⅰ”“Ⅱ”和“Ⅲ”分别代表考虑全部堆渣、部分堆渣和仅考虑碾压堆渣的情况；对计算剖面分别为“冲沟”“右k”和“右d”，分别代表左岸典型坝段冲沟影响、右岸面板连接段k-k剖面和d d剖面的计算分析。

如计算方案编号为“P 2D EB 1-Ⅱ”的计算方案，表明该计算方案为二维计算方案、堆石料采用EB模型、沥青混凝土面板使用弹性模型、使用第1组计算参数组合，考虑部分下游堆渣的影响进行计算。再如“P-3D EB 1-冲沟”的计算方案，表明该计算方案为三维计算方案、堆石料采用EB模型、沥青混凝土面板使用弹性模型、使用第1组计算参数组合，采用左岸典型坝段进行计算分析，研究了左岸岸坡基础冲沟对坝体和沥青混凝土面板应力和应变性状的影响。

8.计算成果

静力计算各种方案结果的典型数值汇总于表4.1-25。

表4.1-25　静力计算结果总表

注 表中最大位移均是指发生在坝体中的最大位移，不包括发生在下游堆渣中的位移。
① 表示顺坡向最大位移值。

9.成果结论

坝后堆渣敏感性分析、二维、三维坝体和面板应力应变分析、沥青混凝土面板黏弹性计算成果分析如下。

（1）坝后堆渣敏感性分析表明：下游堆渣对坝体下游次堆石区的应力和变形有较大的影响，可显著提高坝体下游坝坡的稳定性，对坝体上游主堆石区尤其是沥青混凝土面板应力和变形的影响不大，考虑部分堆渣区的计算工况Ⅱ已基本反映了下游堆渣对坝体变形的影响，可作为三维计算的基本剖面。

（2）二维计算结果表明：

1）主坝坝体变形的分布规律主要受到坝基覆盖层、库底碾压堆渣和次堆石料这三种变形模量较小材料的影响。坝体最大竖直沉降发生在坝体中部，水平位移均指向下游，最大水平位移发生在坝体中部的下游坝坡处，坝体在施工期和蓄水期的最大沉降量为103.1cm和103.9cm，相应最大水平位移为38.4cm和43.3cm。

2）坝体在竣工期和蓄水期的大主应力最大值为1.7MPa和1.85MPa，小主应力最大值为0.8MPa和0.9MPa，坝体剖面中大部分区域的应力水平小于0.65，说明坝体从稳定角度看也是安全的。

3）蓄水期上游面板的挠度在其底部末端最大，其值约为27.4cm；面板底部的反弧段基本为受拉区，倾斜直线段应力和变形均较小，面板顺坡向拉应力、拉应变的峰值均出现在反弧段上部的起点附近，拉应力的峰值为3.41MPa，拉应变的峰值为0.51%。

4）沈珠江双屈服面模型与邓肯张EB模型的二维计算结果相比，所得坝体包括沥青混凝土面板应力和变形的分布规律十分相似，由沈珠江双屈服面模型计算所得坝体变形以及面板变形、应力和应变的数值较小。

5）堆石体变形参数的敏感性计算分析表明，随着堆石体变形模量和强度参数的增加，坝体水平向和竖直向位移均明显减小，沥青混凝土面板的挠度、顺坡向拉应力和拉应变也逐步减小，因此控制上坝坝料质量，提高压实度，是有效的控制坝体变形和减少沥青混凝土面板挠度、最大拉应力和拉应变的手段。

（3）三维条件下坝体和面板的应力变形特性计算结果分析：

1）坝体的最大变形发生在坝体的最大剖面（17-17剖面）处，竣工期坝体中的最大水平位移为42.3cm，发生在下游坝坡的中部；最大竖直位移为103.4cm，发生在下游次堆石中，蓄水期坝体最大水平位移增大为46.5cm；最大竖直位移增大为104.0cm，它们发生的位置和竣工期基本相同。

2）坝体的最大剖面二维、三维计算的坝体沉降变形相差不大，但由于坝体向下游呈反拱状的影响，三维计算结果略大；在三维条件下计算得到的面板变形相对较为均匀，计算得到的最大拉应力和最大拉应变峰值相对较小。

3）坝体左岸坝0+070.00（左岸5-5剖面）计算得到的面板的拉应力和拉应变数值最大，这是由于该处靠近河床部位覆盖层较厚，覆盖层材料含泥量较大，该处坝体下部变形量较大，沥青混凝土面板的位移具有相对较大的变化率，拉应力和拉应变峰值均出现在反弧段与直线段交点附近，顺坡向拉应力的峰值为4.06MPa，顺坡向拉应变的峰值为0.557%，根据计算成果，设计在该部位采取压实或部分置换此处河床覆盖层料，局部的岩石陡岸坡进行适当消坡，以减小此处沥青混凝土面板变形的变化率，降低拉应变的峰值，并在反弧段底部设置加强网格、加厚防渗层。

4）由于库区堆渣并不为坝体的直接组成部分，对坝体及面板应力和变形的计算结果影响较小，但对上水库库底的变形有较大影响，对库区采用堆渣的计算方案，库底在竣工期和蓄水期的最大沉降变形分别为约30cm和80cm，为防止过大不均匀沉降导致黏土铺盖发生裂缝，设计对库盆基础开挖、回填提出了明确的技术要求。

5）沈珠江双屈服面模型与邓肯张EB模型的三维计算结果相比，所得坝体包括沥青混凝土面板应力和变形的分布规律十分相似，但所得数值相对较小。

6）坝体中大部分区域的计算应力水平值小于0.65，从稳定角度看坝体是安全的。

（4）沥青混凝土面板的黏弹性计算分析：

1）对采用柔性沥青混凝土面板的堆石坝，坝体的内部应力及位移的大小和分布主要取决于堆石体的变形特性，面板所采用的模型和参数对其影响不大。

2）当考虑面板沥青混凝土的黏弹性特性时，面板的变形特性主要取决于坝后堆石体的变形，温度和时间对面板的挠度和应变计算结果的影响不大，面板的黏弹性响应主要体现在应力松弛方面。

3）面板沥青混凝土为典型的黏弹性材料，其力学特性对温度的变化较为敏感，一般低温情况仍为面板抗拉设计的控制工况。

4）沥青混凝土的力学性能取决于温度和应变速率，故首次蓄水时间一般应选在气候适宜的条件下进行，以避免首次蓄水坝体变形较大而低温条件下面板变形能力较小所造成的破坏，同时由于沥青混凝土的极限拉应变同应变速率有关，所以应控制水库初次蓄水的速率。

（5）左岸冲沟影响的三维计算分析。在局部三维条件下，水库蓄水期上游面板的挠度在其下部段末端最大，约为38.6cm，坡向拉应力和拉应变的峰值均出现在面板中部附近，顺坡向拉应力的峰值为4.62MPa，顺坡向拉应变的峰值为0.675%。与整体三维计算结果相比，局部三维条件下面板挠度、应力和应变分布规律一致，局部三维计算结果中的面板挠度、应力和应变最大值稍大。

（6）右岸面板连接处二维计算分析。针对k-k、d-d剖面重点计算分析了混凝土廊道两侧由于可压缩层厚度的突然变化对沥青混凝土面板所可能带来的影响。计算结果表明，面板最大挠度为13.6cm，发生在面板底端；面板最大拉应变为0.22%，最大拉应力为1.41MPa，均发生在廊道右上方，对沥青混凝土面板所可能带来的影响有限，施工过程中应注意对廊道两侧堆石料压实质量的控制。

10.可研补充阶段成果结论(www.xing528.com)

2002年可研补充阶段华东院所做坝体应力应变计算采用河海大学研制的BCF平面有限元比奥固结程序平面非线性有限元程序，沥青混凝土及填筑料的本构模型均采用邓肯-张E-μ模型并考虑卸荷影响，采用中点增量法求解此非线性问题，并用逐级加荷模拟土石坝施工与运行过程。

网格中共分8种材料类型，共计单元194个，结点216个。

荷载分级：

第一级，荷载为地基；

第二级至第八级，坝体土石料六级施工；

第九级，沥青混凝土面板施工；

第十级，库区黏土填筑；

第十一级至第十三级为水荷载；

水荷载分三级。

748.00→758.00　（第十一级）；

758.00→773.30　（第十二级）；

773.30→789.60　（第十三级）。

计算参数参照类似工程及其他有关资料，拟定材料设计参数及成果见表4.1-26～表4.1-28。

表4.1-26　材料设计参数表

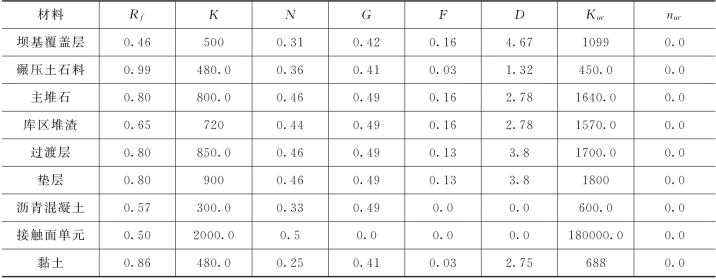
表4.1-27　材料设计参数表

表4.1-28　二维有限元应力应变计算成果表

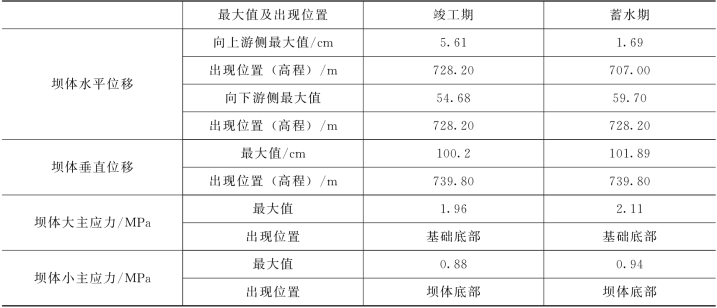
面板变形及应变：蓄水后面板的挠度随着水压力的增加而增加，底部最大垂直位移为14.79cm，挠跨比为0.13%。沥青混凝土护面与库底连接部位的最大拉应变较大，约为3.78×10-3。

与施工阶段最大断面平面计算成果比较：垂直位移计算值基本一致，水平位移较施工阶段计算值偏大，面板了拉应变偏小，这和材料参数的选择有直接的关系。

11.主要计算成果与监测成果对比分析

截至2007年12月5日，预埋土体位移计读数正常，观测到的坝体最大水平位移量170mm，见图4.1-8。

图4.1-8　主坝水平位移观测值

蓄水期最大水平位移量为175mm，于2008年5月16日测得。

有限元二维计算的竣工期和蓄水期最大水平位移为分别为38.4cm和43.3cm，发生在下游坝坡的中部；三维条件下竣工期和蓄水期最大水平位移为分别为42.3cm和46.5cm，与观测结果比较，计算值偏大。

4.1.5.3　主坝动力有限元计算

静力计算程序可进行土石坝和面板堆石坝的动力反应分析，本构模型采用沈珠江提出的非线性黏弹性模型，分析方法采用分段等效线性化方法。这一方法的基本思想是，把整个地震过程分成若干个时段，对每个时段，先假定动剪模量和阻尼比，采用逐步积分的分析方法，时间差分按Wilson法进行；在该时段计算得到的动剪应变可能与假定的动剪模量和阻尼比不匹配，因而需进行2～3次迭代；在该时段结束后按经验公式计算出该时段内各单元残余变形增量，并把它们转换成初应变或初应力后进行静力计算，得出节点位移、单元应变和应力的变化。如此逐个时段进行计算，就能得出整个过程的动力应力应变和变形的发展过程。

1.输入地震波

根据《混凝土面板堆石坝设计规范》（DL/T 5016—1999）和《水工建筑物抗震设计规范》（DL 5073—2000）规定：设计烈度为8度以上坝高大于70m的土石坝，应采用拟静力法进行抗震稳定计算，同时用有限元法对坝体、坝基进行动力分析，综合判定其抗震安全性。

动力计算中采用的地震波输入时程曲线共3组，分别简称为坝址波、规范波和实测波，每组地震波含顺河向、横河向以及竖直向3条地震波。其中规范波为根据《水工建筑物抗震设计规范》（DL 5073—2000）的规定由人工合成得到的地震波，坝址波由类比工程得到，实测波为澜沧耿马实测地震波。

各输入地震波顺河向分量峰值加速度均为2.00m/s2；坝址波在坝轴向和竖直向的峰值加速度分别为1.92m/s2和1.28m/s2；规范波在坝轴向和竖直向的峰值加速度分别为2.11m/s2和1.34m/s2；实测波在坝轴向和竖直向的峰值加速度分别为1.04m/s2和0.57m/s2。坝址波的持续时间为13s，加速度较大的时间范围约8s；规范波的持续时间为20s，加速度较大的时间范围约17s；实测波持续时间为15s，加速度较大的时间范围约5s。

2.动力计算材料参数及方案组合

动力计算采用沈珠江建议的修正非线性黏弹性模型，动力反应计算部分包含有5个模型参数，分别为k1、n、k2、μd和λmax；残余变形计算部分包括有5个模型参数，分别为c1～c5。

材料动力计算参数的基本参数组合见表4.1-29，其中主堆石料、次堆石料、二种坝基覆盖层料、垫层料、过渡料和排水带料共7种坝料的动力计算参数根据大型动三轴试验结果确定，其他材料的动力模型计算参数由工程类比根据经验得到。

表4.1-29　动力反应分析材料参数组合1-基本参数

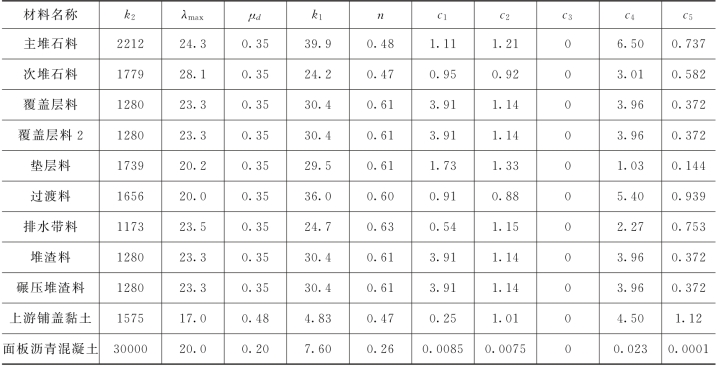
注 覆盖层料2为左岸坝基覆盖层料，含石量取40%。

材料参数的选取对计算结果影响很大，考虑到试验结果具有一定的离散性和随机性，可能与实际工程中的材料特性具有一定差异；另外对如面板沥青混凝土等材料其动力计算参数在文献中可供参考的资料较少，因而针对计算参数进行敏感性分析。

3.动力计算方案

由于计算的方案较多，为了表述的方便，对动力计算定义了一套计算方案的编号规则，见表4.1-30。动力计算方案的编号由计算维数、动力计算的材料参数组合和输入地震波名称复合而成。

表4.1-30　动力计算方案及计算内容一览

P+“-计算维数”+“-动力材料参数组合号”+“-输入地震波组合号”。其中：P：“Plan”的简写，代表方案；

计算维数：为“2D”和“3D”，分别代表二维和三维有限元动力计算；

动力材料参数组合号：计算中使用的动力材料参数的组合，具体见表4.1-31；

输入地震波组合号：为“G”、“B”或“S”，分别代表输入地震波为规范波、坝址波和实测波。

表4.1-31　敏感性分析参数组合

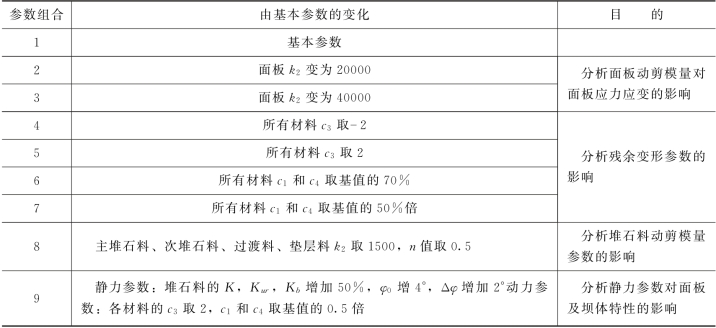
4.二维有限元分析

（1）坝体反应分析。二维动力反应分析各基本计算方案计算结果见表4.1-32。

表4.1-32　二维动力计算坝体反应（动力参数组合1）

注 动力参数组合基于静力计算基本参数组合。

坝体动应力分析结论如下：

1）从最大加速度放大系数等值线分布图可以看出，加速度反应在坝体内总体反应较弱，但在接近坝顶和堆渣内时有所放大。

2）在覆盖层和排水带内加速度放大系数减小较快，特别是顺河向加速度放大系数，覆盖层和排水带起到了一定的减震作用。

3）各种地震波作用下坝体内产生的残余变形整体较大。其中，坝址波引起的坝体残余变形最大，其次是规范波，实测波引起的坝体残余变形最小。

4）由残余变形后的轮廓图可以看出，地震后坝体上游、库底和下游堆渣部位有较大的震陷。

5）下游堆渣区的各种反应和库底堆渣内的竖向反应较大。

（2）面板反应分析。各种地震波作用下二维动力计算的面板应力和变形的最大值列于表4.1-33。

表4.1-33　二维动力计算面板反应最大值（动力参数组合1）

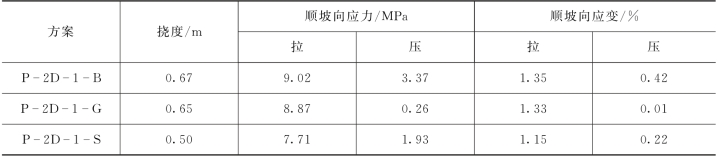
分析结论如下：

1）在地震作用下面板挠度、顺坡向拉应力和和拉应变同原静力方案的计算结果相比均有较大的增加。

2）在叠加地震所导致的面板挠度后，面板的总挠度分布较为均匀，最大拉应力和拉应变的最大值均发生在面板下部的反弧段，与静力计算发生的位置基本一致。

5.三维有限元分析

三维动力反应分析各基本计算方案计算结果见表4.1-34和表4.1-35。

表4.1-34　三维动力计算坝体内反应（动力参数组合1）

表4.1-35　三维动力计算面板反应最大值（动力参数组合1）

由三维动力反应分析所得到的最大加速度放大系数在坝体剖面上的分布规律同二维计算基本相同，数值略大于二维计算成果。

6.参数敏感性分析

各方案坝体和面板反应的参数敏感性分析计算结果见表4.1-36和表4.1-37。

表4.1-36　二维动力计算参数敏感性分析坝体反应

表4.1-37　二维参数敏感性分析动力计算面板反应最大值

分析结论如下：

（1）面板模量参数k2对坝体总体动力计算结果的影响不大。

（2）材料残余体变指数c3降低（残余体应变随应力水平增加而变大），坝体中的最大加速度放大系数和残余变形均有较大增加，面板最大挠度、顺坡向拉应力和压应力有所增加。

（3）随着残余体变和残余剪应变系数c1和c4的降低，坝体的残余变形均有所减小，顺河向加速度放大系数稍有减少，竖直向加速度放大系数变化不大；面板挠度有所减小，顺坡向拉应力和拉应变几乎没有变化，顺坡向压应力稍有增加。

（4）坝料的动剪模量参数降低后，坝体加速度放大系数有所减小，残余变形稍有增加，这与上述材料参数变化后坝体的整体刚度减小，动模量降低有关。

（5）动剪模量的变化对面板挠度、顺坡向拉应力和拉应变的影响不大，顺坡向压应力和压应变有所增加。

（6）材料静力参数对坝体和面板的动力反应有较大的影响，其原因是静力参数变化使得作为动力计算起点的静力状态发生了变化。

（7）当输入地震波的峰值增大后，计算所得坝体的最大加速度放大系数有所减小，残余变形稍有增加，面板挠度和顺坡向拉应力拉应变变化不大，顺坡向压应力和压应变有所增加。

4.1.5.4　坝体有限元稳定分析

抗剪强度折减有限元法利用弹塑性有限元法求取边坡等土工结构物的整体安全系数。

1.计算条件

计算采用抗剪强度折减有限元法进行坝体边坡的二维和三维稳定分析，计算参数见表4.1-38，其中主堆石料、次堆石料、覆盖层料、覆盖层料2、垫层料、过渡料和排水层料7种坝料的强度参数c′和φ′根据大型三轴试验结果确定。

表4.1-38　材料计算参数表

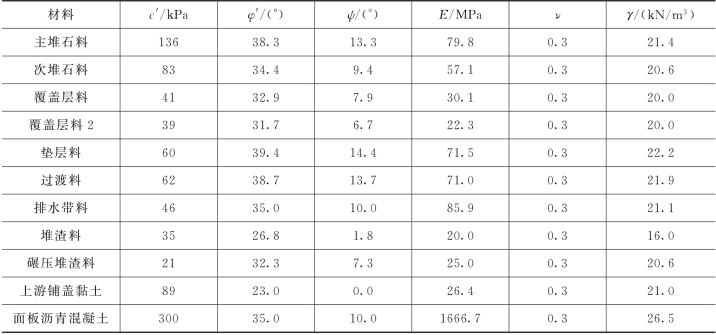
注 覆盖层料2为左岸坝基覆盖层料，含石量取40%。

计算中未考虑地震的影响，计算剖面分两种情况：

（1）考虑部分下游堆渣的影响，其具体采用的计算剖面与静力计算的剖面Ⅱ相同。

（2）不考虑下游堆渣和下游碾压堆渣的影响，采用仅考虑坝体本身的计算剖面，以下称为计算剖面Ⅳ。

2.计算成果及分析

用抗剪强度折减有限元法进行边坡稳定分析的优点包括：不需假定潜在滑裂面的形状和位置，计算中能自动找出潜在的滑裂面；能考虑土与结构物的相互作用及塑性变形，因而能计算较复杂的边界及荷载条件，且能根据变形协调条件进行应力调整。

表4.1-39　稳定分析计算结果

从表4.1-39可以看出，采用计及条块间作用力的计算方法时，正常运用条件下1级建筑物坝坡稳定最小安全系数为1.50，两剖面计算均满足设计要求。