应用纳米压痕法进行材料性能测试

1.电沉积镍镀层残余应力的测量

利用NanoIndenterⅡ纳米压痕仪加载得到电沉积镍镀层的载荷-位移曲线，并对镍镀层中的残余应力进行计算^[1]。

（1）试验材料及方法 电沉积镍镀层为普通镀镍带（镀层厚度约为17μm）、普通T处理镀镍带（镀层厚度约为2μm，450℃）、再结晶处理镀镍带（镀层厚度约为17μm，620℃）、普通T处理轧制带（镀层厚度约为2μm，3%的轧制变形）、再结晶处理轧制带（镀层厚度约为17μm，3%的轧制变形）。选取厚度为0.05mm、纯度为99.99%的镍箔作为无应力状态的镍镀层。

试验过程包括以下6个步骤。

1）压头逼近试样表面，确定表面的接触零点。

2）以10nm/s的速率加载至最大载荷。

3）在最大载荷3.5mN时保持10s，以减小蠕变对卸载位移的影响。

4）以10nm/s的速率卸载至最大载荷的90%。

5）在最大载荷的90%保持100s，获得仪器的热漂移速率，对试验数据进行热漂移校正。

6）以10nm/s的速率将载荷从最大载荷的90%卸载到零。对每个试样压入5次，取平均曲线进行计算。

（2）试验结果 图4-1～图4-5分别是普通镀镍带与镍箔、T处理镀镍带与镍箔、再结晶处理镀镍带与镍箔、T处理轧制带与镍箔、再结晶处理轧制带与镍箔的载荷-位移曲线。普通镀镍带、T处理镀镍带内的残余应力为拉应力，再结晶处理镀镍带、T处理轧制带、再结晶处理轧制带内的残余应

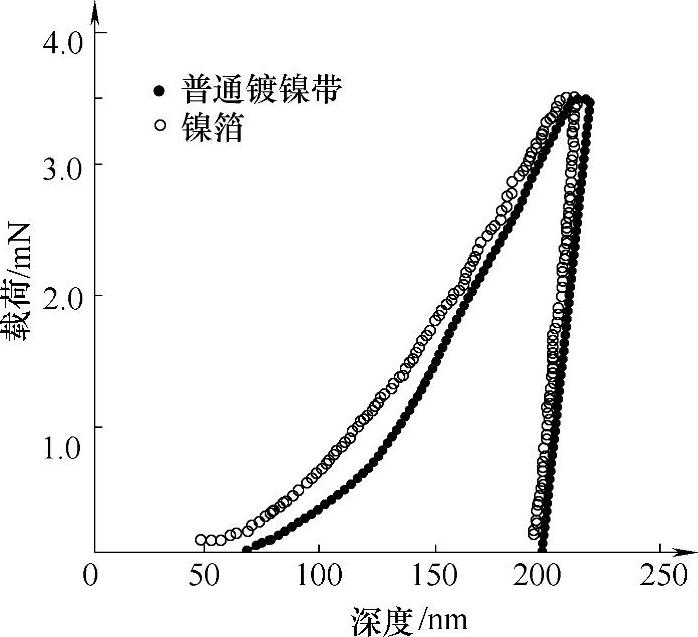
图4-1 普通镀镍带与镍箔的载荷-位移曲线^[1]

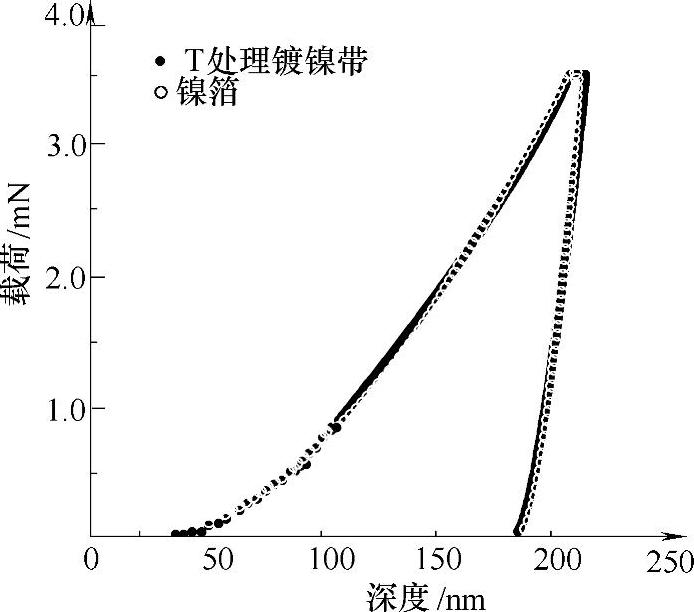
图4-2 T处理镀镍带与镍箔的载荷-位移曲线^[1]

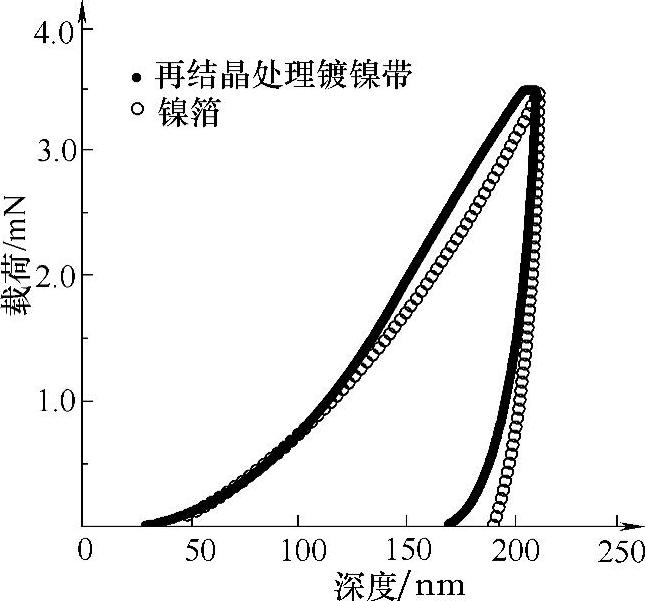
图4-3 再结晶处理镀镍带与镍箔的载荷-位移曲线^[1]

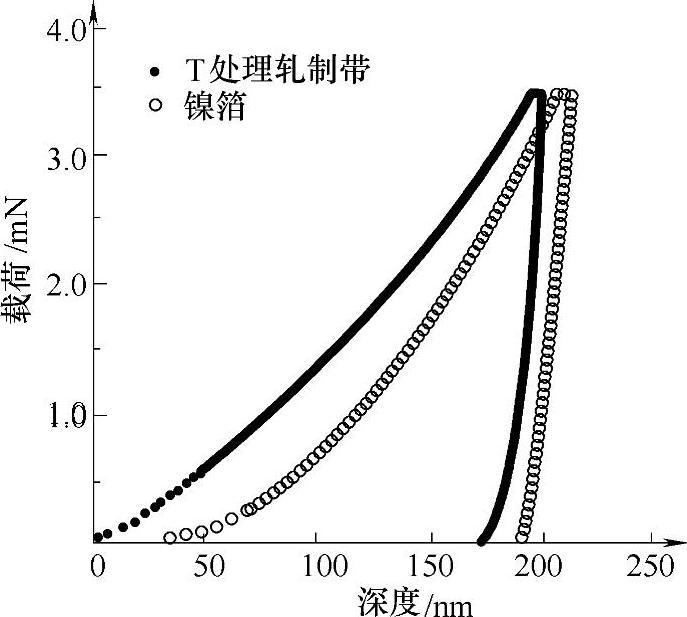
图4-4 T处理轧制带与镍箔的载荷-位移曲线^[1]

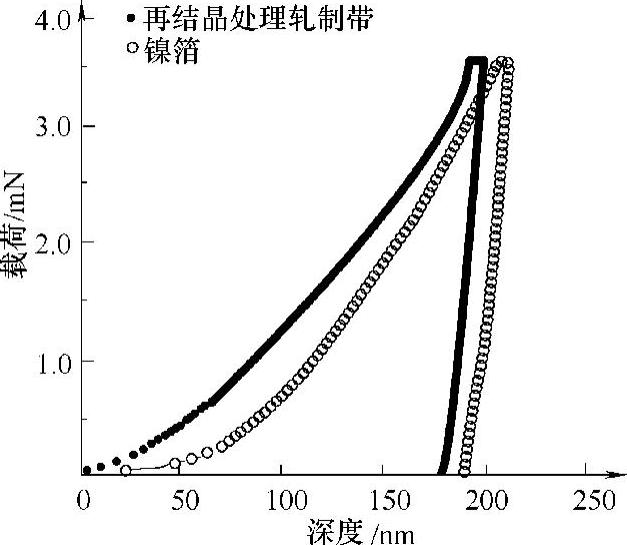
图4-5 再结晶处理轧制带与镍箔的载荷-位移曲线^[1]

力为压应力。将所有试样的纳米压痕试验参数和用Suresh理论模型^[2]计算出的残余应力结果列于表4-1中。

表4-1 5种电沉积镀镍层的试验和计算结果^[1]

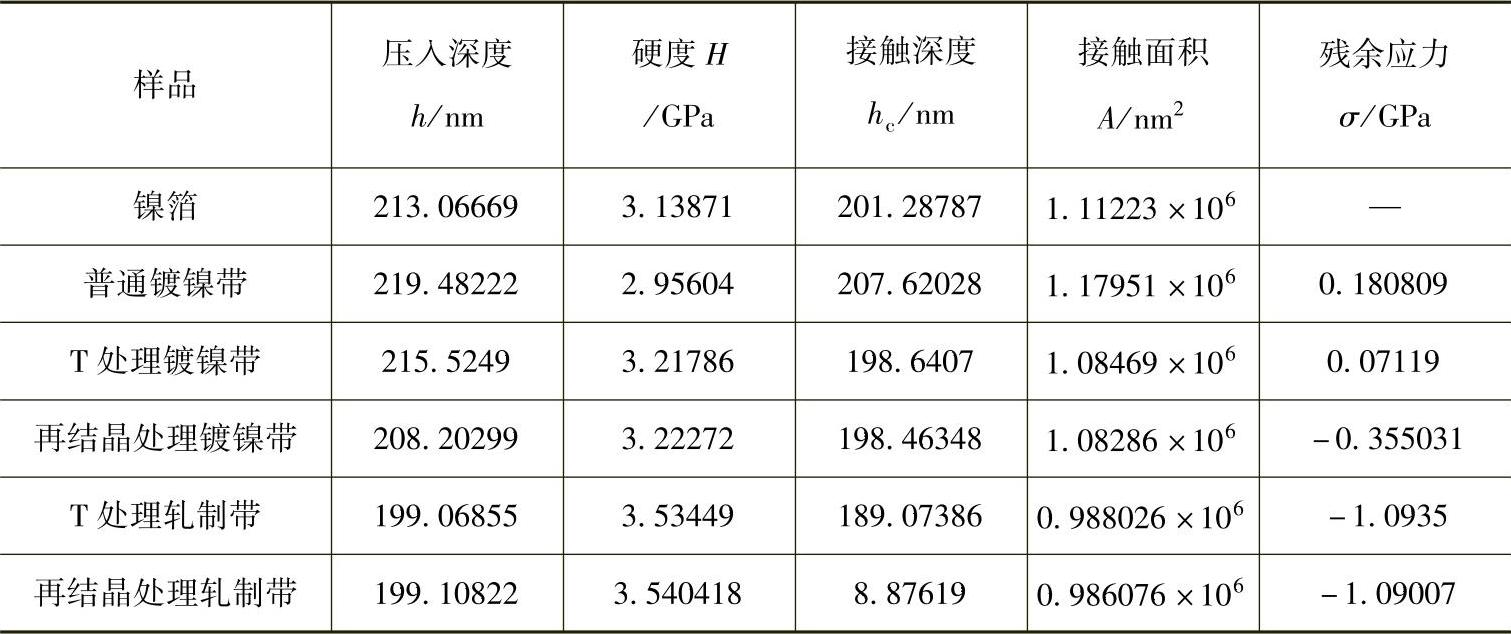
5种样品的硬度与镍箔相差不大，符合纳米压痕法测量残余应力的前提条件。未经处理的普通镀镍带中存在较大的残余拉应力，T处理能够减小镍镀层的残余应力（T处理镀镍带与镍箔的载荷-位移曲线相近，这说明其内部残余应力较小，如图4-2所示）。轧制后的T处理镀镍带的残余应力变为压应力，再结晶处理使得镀层的拉应力变为压应力，轧制后的再结晶处理镀镍带中的压应力变大。因为镀层的疲劳破坏和应力腐蚀破坏主要是应力集中引起的，所以在材料表面预先产生压应力能够显著提高材料的使用寿命。因此，普通镀镍带在经过T处理轧制或再结晶处理轧制后质量能够得到显著地提高。

2.离子注入残余应力的测量

离子注入法作为一种表面处理技术，被广泛地用来提高金属表面的力学性能。由于离子、原子间的相互作用，以及靶材基体与离子注入层之间的热膨胀不匹配，在离子注入过程中会引入残余应力。离子注入层一般为微米级或亚微米级，因此，纳米压痕技术被广泛用来表征离子注入层的力学性能，特别是残余应力的测量。

采用纳米压痕技术测量离子注入过程中引入的残余应力，分别对试样的离子注入和无离子注入区域进行纳米压痕试验，分析残余应力与离子注入后压痕载荷变化的关系。通过这种关系计算出离子注入后引入的残余应力，计算得到的残余应力与有限元模拟结果一致^[3]。

（1）试验材料及方法 试样从2mm厚的商用不锈钢SUS304-CSP（相当于06Cr19Ni10）板上切割下来。该板的化学成分（质量分数，%）为：C 0.05，Si 0.62，Mn 0.80，P 0.031，S 0.002，Cr 18.12，Ni 8.14，剩余为Fe。用NEC串联珠链式静电加速器，将3MeV Fe²⁺注入不锈钢板中。离子注入后，在室温下，用纳米压痕仪（Berkovich压头）对不锈钢板的离子注入和无离子注入区域进行压痕试验。压痕载荷逐渐增大到预设值，然后减小到0（完全卸载）。记录出每个压痕的载荷-深度曲线。在相同位置分别对离子注入和无离子注入区域进行10次压痕试验（加载和卸载）。利用平均压痕载荷-深度曲线计算出离子注入引入的残余应力值。

压痕表面为等双轴残余应力，且沿压痕深度方向均匀分布。图4-6所示为用来计算残余应力的有应力和无应力试样的加载和卸载曲线。残余应力的计算公式为

式中，F₁为有应力试样的最大载荷；F₂为无应力试样的最大载荷；α为残余压痕的半锥角，可以作为其他压头的几何校正因子，α可以从有限元模拟和纳米压痕试验的最佳拟合中估算出来；h_r为残余压痕深度。

（2）试验结果 通过拟合试验曲线与有限元模拟结果，几何校正因子α为65.3°。采用试验数据（F₁=36mN，F₂=33mN，h_r=40nm），则用式（4-1）计算出的残余压应力为631MPa。

对离子注入和无离子注入不锈钢板进行10组压痕试验，所得到的载荷-深度曲线如图4-7所示。由该图可以看出，离子注入引入的为压应力，因为压痕深度相同时，穿透离子注入表面所需的载荷较大。这与位错强化模型的预测一致。有报道说，原子/离子注入过程中，离子具有向前的冲力并转移到晶格，这种效应导致了位错强化，并在离子注入表面产生压应力。

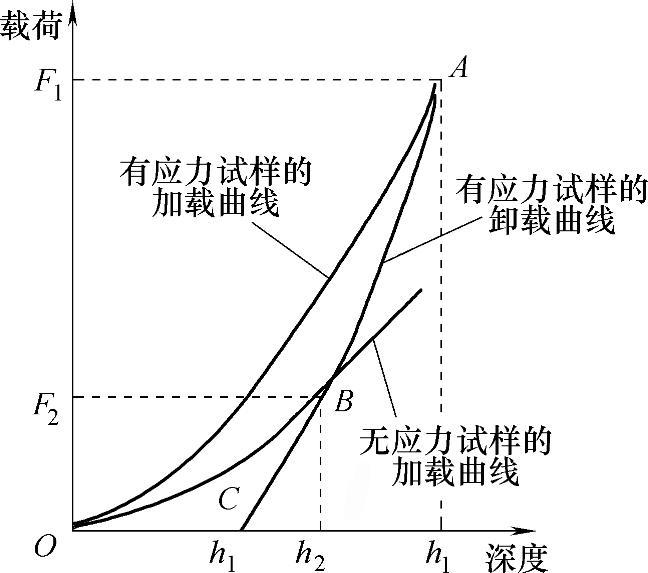
图4-6 用来计算残余应力的有应力和无应力表面的加载和卸载曲线^[3]

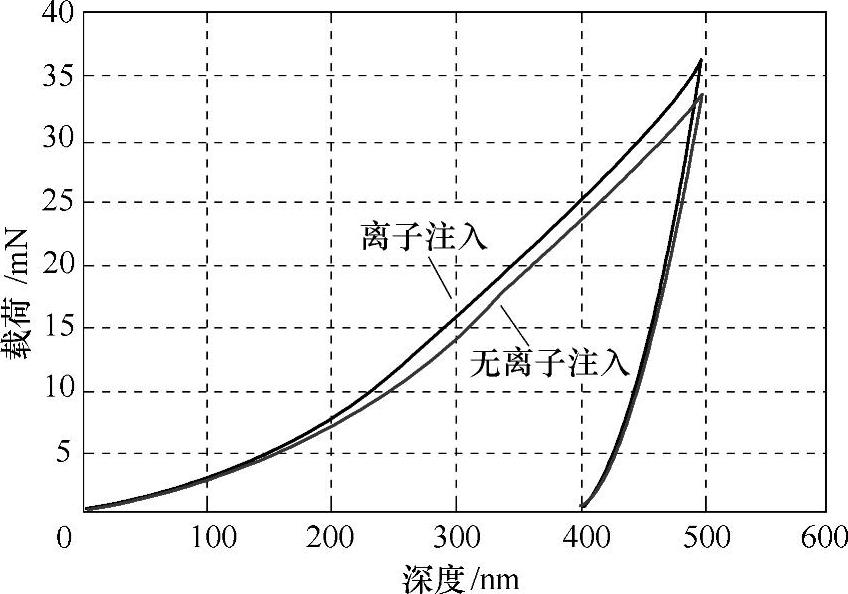
图4-7 离子注入和无离子注入不锈钢板的载荷-深度曲线^[3]

3.复合材料残余应力的测量

用纳米压痕技术（球形压头）测量了具有代表性的Al基复合材料的残余热应力，证实了用纳米压痕技术对多相组分材料的残余应力进行局部性测量的可行性^[4]。

（1）试验方法 采用未增强和SiC增强的（体积分数为10%、20%、30%）Al-Cu-Mg合金作为试验材料，将它们分别用2080、2080/SiC/10p、2080/SiC/20p和2080/SiC/30p表示。所有材料由粉末冶金和挤压工艺制备。挤压后，2080/SiC/10p、2080/SiC/20p和2080/SiC/30p增强颗粒的平均尺寸分别为6μm、6μm、23μm。图4-8所示为具有代表性的2080/SiC/20p复合材料的金相照片。将未增强合金和复合材料在493℃加热2h，然后再进行水淬。这种热处理是复合材料中产生残余热应力的主要原因。为了防止室温下的沉淀生成，将淬火后的试样储存在制冷器中，随后进行加工、抛光和试验。

图4-8 2080/SiC/20p复合材料的金相照片^[4]

用带有球形压头的XP纳米压痕仪对SiC颗粒间的Al基体压痕。压头由金刚石制成，压头的实际半径为（9.5±0.3）μm，深度为30～50nm。纳米压痕试验采用固定载荷模式，位移和载荷分辨率分别为0.01nm和50nN。施加固定载荷的速率为25μN/s；在最大载荷处保持15s，在相同的速率下进行卸载，直到载荷被完全移除。每个试样采用3个载荷最大值：1mN、2mN和3mN。在每个试样每个载荷下进行8～15次压痕试验。由于载荷相对较低，未对数据进行热漂移校正。然而，试验前设定的热漂移临界值小于0.05nm/s。

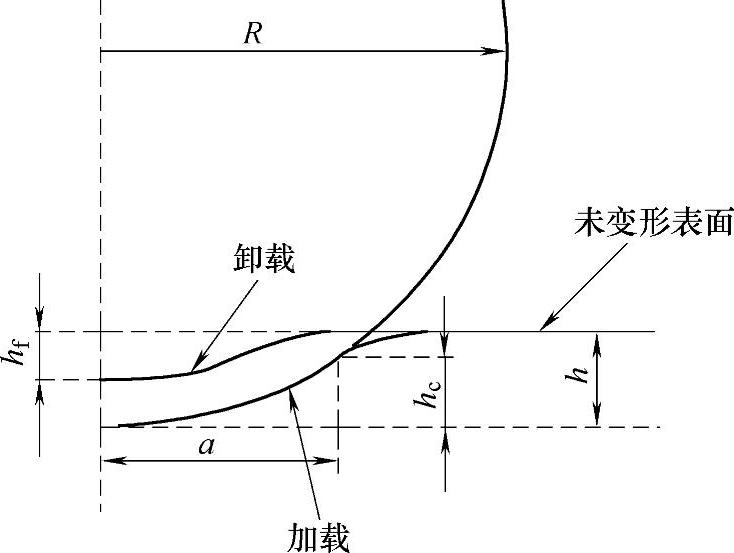
图4-9 压痕几何参数^[4]

（2）理论分析 用外推法估测后屈服状态的球形压痕数据来测量开始屈服时的接触半径。需要已知材料的屈服强度，就可基于封闭型分析法，计算出双轴应力。有关几何参数如图4-9所示，图中R为压头半径，a为接触半径，h为压载过程中的总压痕深度，h_c为加载过程中的接触深度，h_f为卸载时的残余压痕深度。压痕过程中，当a小于R时，初始屈服阶段可以采用典型的Hertz接触理论。

总深度h与接触半径a的关系为

外加载荷F与h之间的关系为

式中，E_e为有效弹性模量，可以表示为

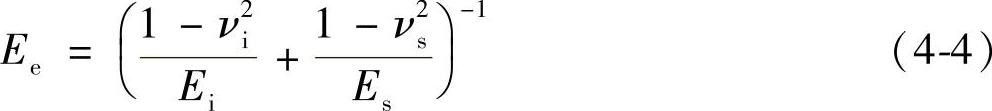
式中，E和ν分别为弹性模量和泊松比，下角标i和s分别代表压头和试样。平均接触应力，定义为总载荷与投影面积的比值，由式（4-2）和式（4-3）得

该方法需要测量出以下参数：压痕载荷最大值F_max、最大压痕深度h_max、最终接触深度h_f和接触半径a。F_max和h_max可以从载荷-位移数据中直接获得。h_f的测定过程是基于：压痕卸载是由另一个半径为R₂的球形接触压痕产生的半径为R₁的球形弹性卸载。卸载数据可以表示为

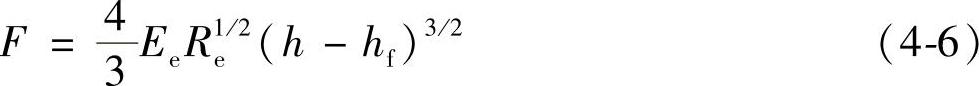
式（4-6）是式（4-3）的修正形式，R_e是与R₁、R₂有关的有效半径。h_f是通过拟合卸载曲线上部的90%而得到的。注意R₂同样是未确定的，被看成是回归分析中的一个未知数。

为测定接触半径a，再次用到基于Hertz接触理论的结果。接触深度可以表示为

则接触半径可以从压头的几何尺寸中得到，即

a=（2Rh_c-h²_c）1/2 （4-8）(www.xing528.com)

该方法需要知道开始屈服时的平均接触应力。开始屈服时的接触半径需要从试验中得到，即通过不同载荷下测量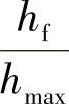与非量纲参数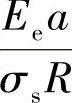之间的关系得到（σ_s为被测材料的屈服强度）。因为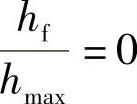表示完全弹性变形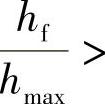，时，塑性变形开始，因此在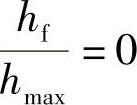时的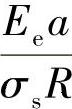值表示屈服开始，可用来测量这个临界点的接触半径a₀。之前的数学分析已经显示了在弹塑性过渡区的较宽范围内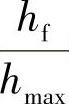，和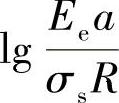呈近似线性关系。因而，通过外推离散的数据，将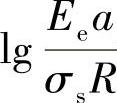设为0，则可得到a₀。

现在只剩下将σ_m与屈服状态联系起来。在弹性区内，距离压头表面深度约0.5a的地方，球形压痕的最大切应力约为0.47σ_m。将最大切应力设为0.5σ_s，则得到σ_m=1.06σ_s。当材料中存在双轴残余应力σ_r时，根据Mises或Tresca屈服准则将得出以下接触应力的表达式：

σ_m =1.06（σ_s-σ_r） （4-9）

只要沿着对称轴发生亚表面屈服，则由式（4-5）和式（4-9）可得

如果已知被测材料的σ_s，则通过测量出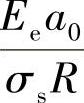，即可得出残余应力。铝合金2080基体的屈服强度为390MPa。计算E_e所需要的弹性常数为：E_s=74GPa，v_s=0.33，E_i=1140GPa，v_i=0.07。

（3）试验结果 将每种材料的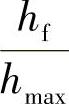的3个点（对应压痕载荷的3个最大值）和它们各自的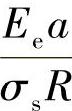值绘成曲线，如图4-10所示。通过对数回归以y=Alg（x）+B进行曲线拟合，其中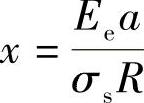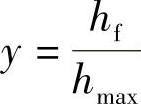，。通过外推法线性拟合为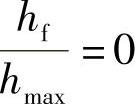，则得到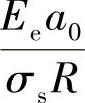值。由式（4-10）计算，2080、2080/SiC/10p、2080/SiC/20p和2080/SiC/30p的残余应力分别为6.36MPa、152.8MPa、161.3MPa和268.8MPa。

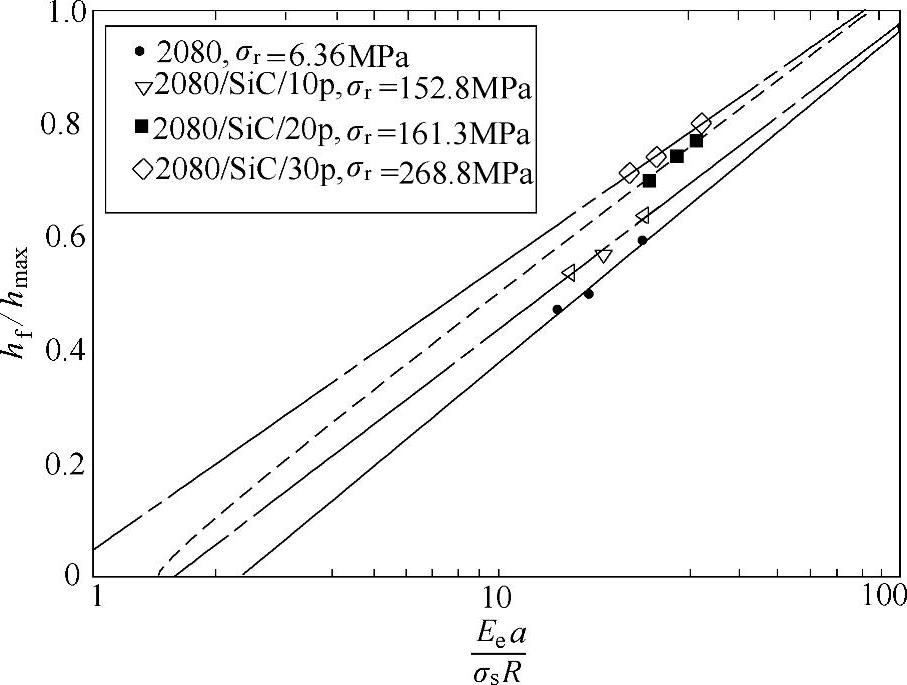
图4-10 四种材料的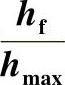随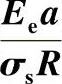的变化^[4]

4.陶瓷薄膜残余应力的测量

用传统的X射线衍射法和压痕技术测量了CrN、MoN、ZrN和Zr四种不同陶瓷薄膜的残余应力^[5]。用压痕法测得的陶瓷薄膜的残余应力是X射线法测得的3倍多。通过将Suresh模型中Vicker锥形压头的几何因子设为1可以消除这种差异。

通过电弧物理气相沉积（PVD）在高速工具钢上沉积了CrN和MoN薄膜，在冷作工具钢上沉积了ZrN和Zr。压痕试验的压入载荷为25mN，产生的压痕深度小于薄膜厚度的10%。对于每种薄膜，至少进行10次重复测量。采用传统的X射线衍射法也测量了四种陶瓷薄膜中的残余应力。

压痕法计算残余应力σ_r的公式为

A/A₀=[1+（σ_rf/σ_m）]^-1 （4-11）

式中，A和A₀为有应力和无应力时的压痕接触面积；f为几何因子，f=sinα，式中α与压头的压痕角有关，如果Vicker锥形压头的α=22°，则f=0.375。σ_m为平均接触应力或等同于硬度。

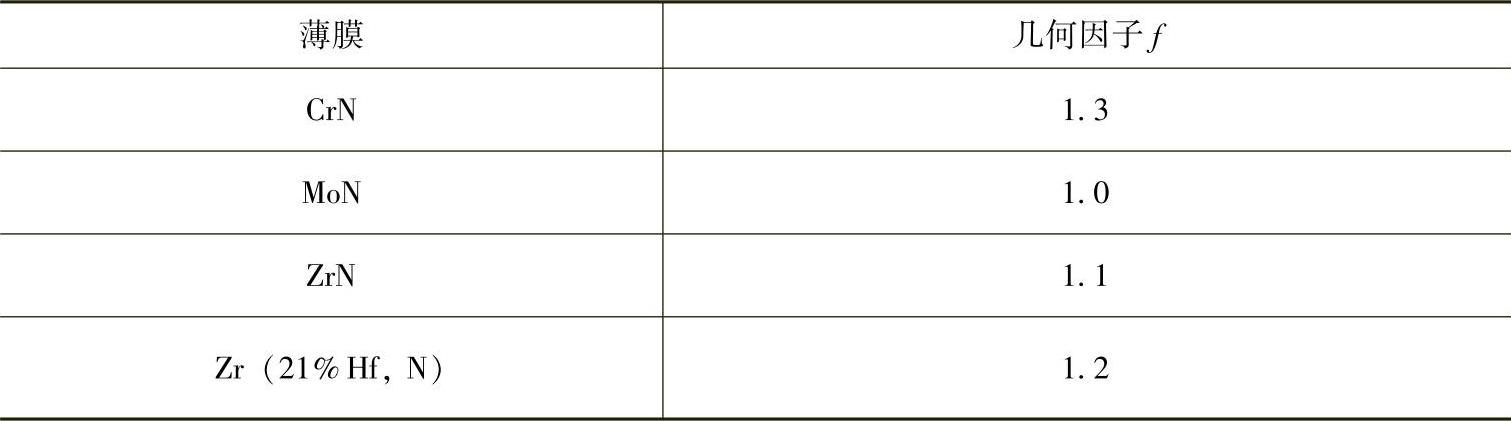
表4-2列出了根据传统的X射线衍射法测得的CrN、MoN、ZrN和Zr四种陶瓷薄膜的残余应力值，以及根据压痕法用式（4-11）计算的残余应力值。用压痕法测得的陶瓷薄膜的残余应力是X射线衍射法测得的3倍多。由于传统的X射线衍射法已经被广泛用于薄膜，且很成熟，因此认为这种高估值来自于式（4-11）中的f值。在残余应力计算中f取0.375。因此，通过将X射线衍射法得到的应力值代入式（4-11），计算出压痕法的几何因子f，如表4-3所示。几何因子计算为1，对应于α值为90°。因此，如果对于Vicker锥形压头，测量压痕法的理论方程式（4-11）修正为：A/A₀=[1+（σ_r/σ_m）]^-1，则可以得到与X射线衍射法近似的残余应力值。

表4-2 根据传统X射线衍射法和压痕法得到的陶瓷薄膜残余应力值^[5]

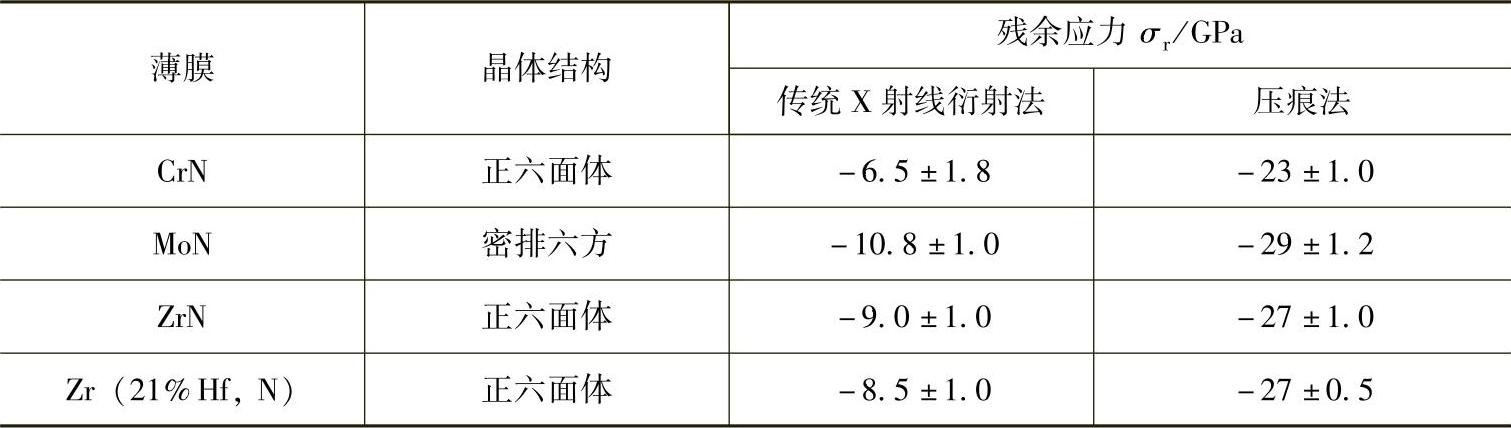
表4-3 试验计算得到的几何因子值^[5]

5.等离子熔覆Fe314涂层的残余应力测量

（1）试验方法 基底材料为Q235钢，熔覆结束后获得Fe314熔覆层的厚度大约为2mm^[6-8]。将制备获得的微弧等离子熔覆Fe314涂层试样平均分为四组，第一组保持原熔覆状态，编号为1号；其他三组分别置于SX-4-10M型箱式电阻炉中进行退火处理，温度分别设定为500℃、600℃、800℃，保温时间均为1h，之后随炉冷却，编号分别为2号、3号和4号。分别使用400#、600#、800#、1000#、1200#砂纸对所有试样的熔覆层表面进行打磨处理，随后在抛光机上进行抛光处理。使用纳米压痕仪XP系统对微弧等离子熔覆Fe314涂层（包括1号未处理、2号500℃退火、3号600℃退火、4号800℃退火）进行了固定压痕深度分别为200nm、350nm、610nm、860nm、1050nm的压痕试验；另外对1号和3号试样进行了固定载荷为20mN、50mN、100mN、150mN、200mN的压痕试验，将2号经过600℃退火的试样作为无应力状态样品。使用S.Suresh模型及Yun-Hee Lee模型进行固定压痕深度及固定载荷的残余应力计算。

（2）试验结果 对载荷-位移曲线进行分析计算，结果如表4-4～表4-9所示。根据两种压痕模型的残余应力测量结果，绘制出不同涂层残余应力随压痕深度及载荷的变化分别如图4-11～图4-13所示。

表4-4 1号未处理熔覆层不同压痕深度时的力学性能^[6]

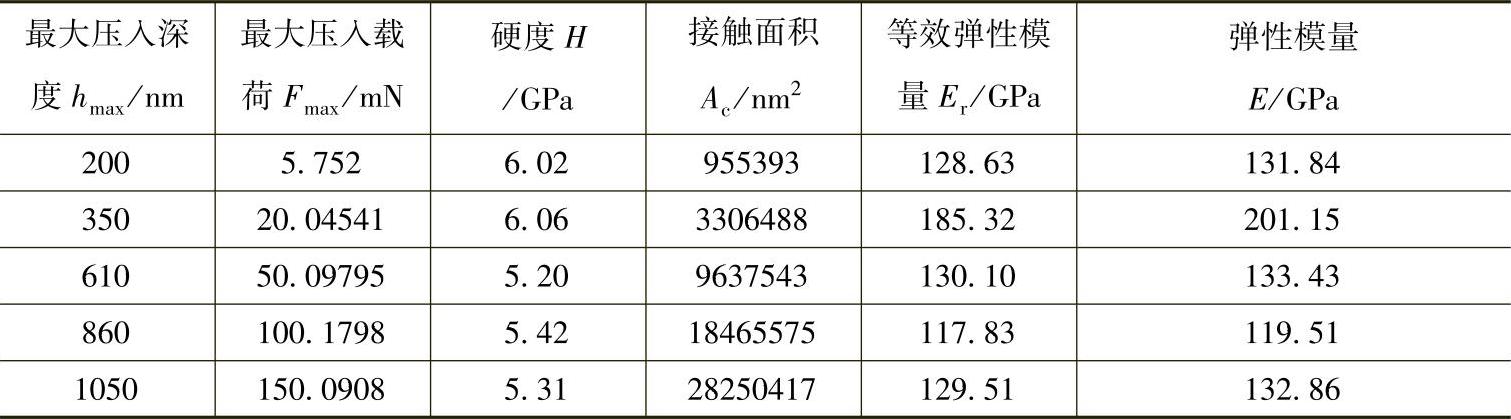
表4-5 1号未处理熔覆层不同压痕深度时的残余应力^[6]

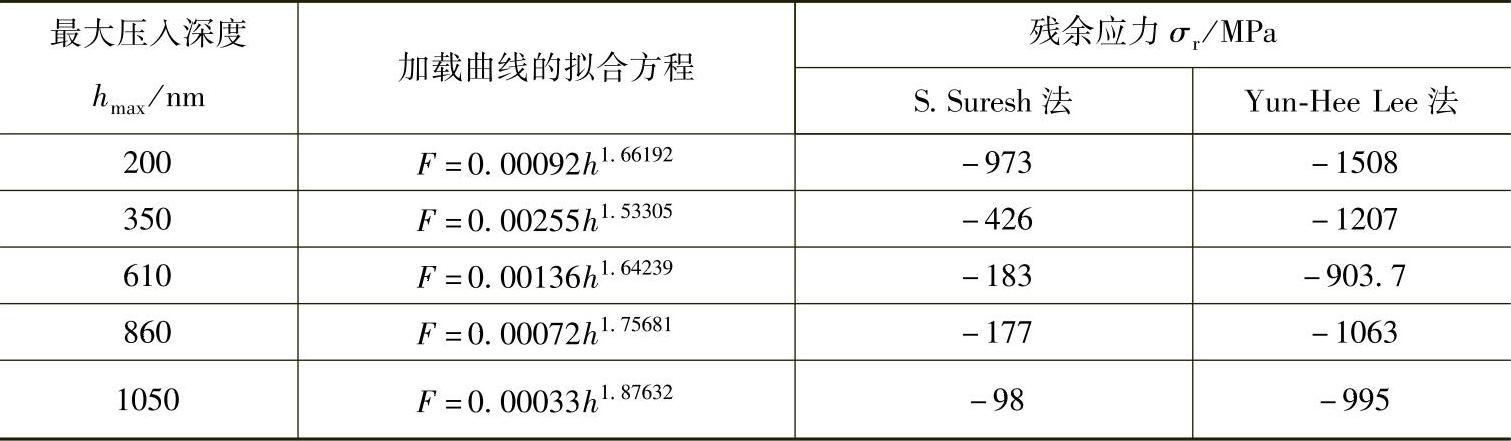
表4-6 1号未处理熔覆层不同载荷时的力学性能^[6]

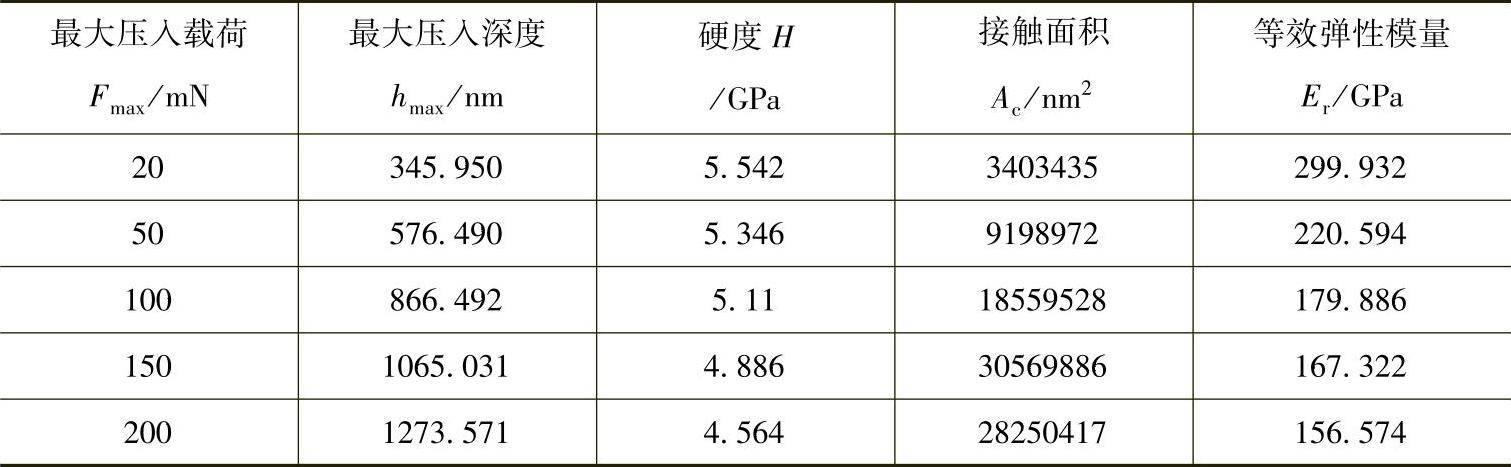
表4-7 1号未处理熔覆层不同载荷时的残余应力^[6]

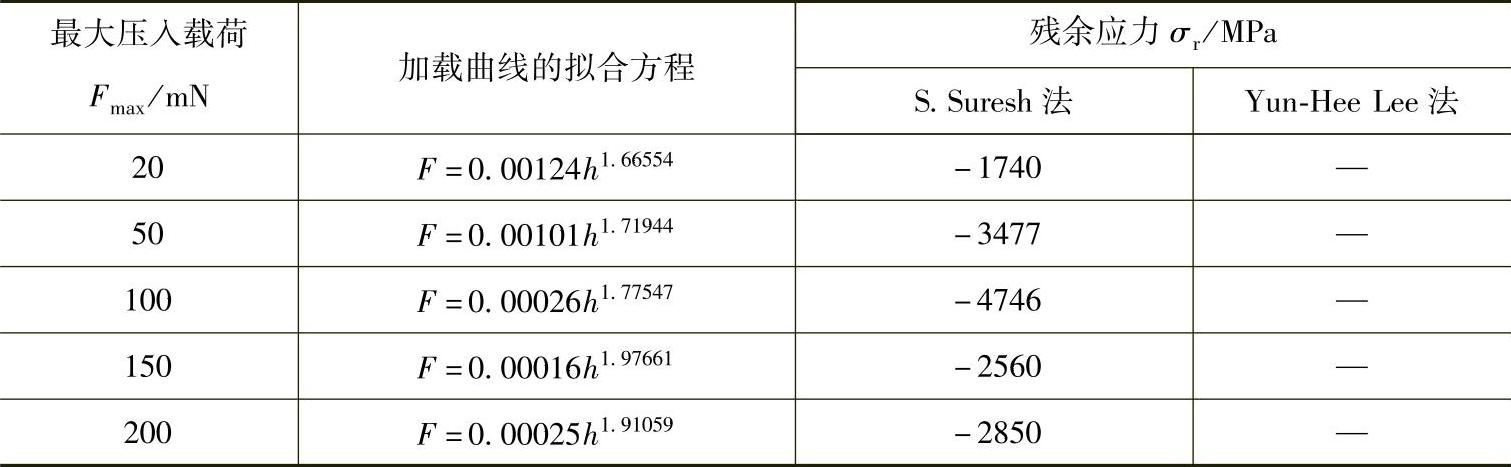
表4-8 2号500℃退火熔覆层不同压痕深度时的力学性能^[6]

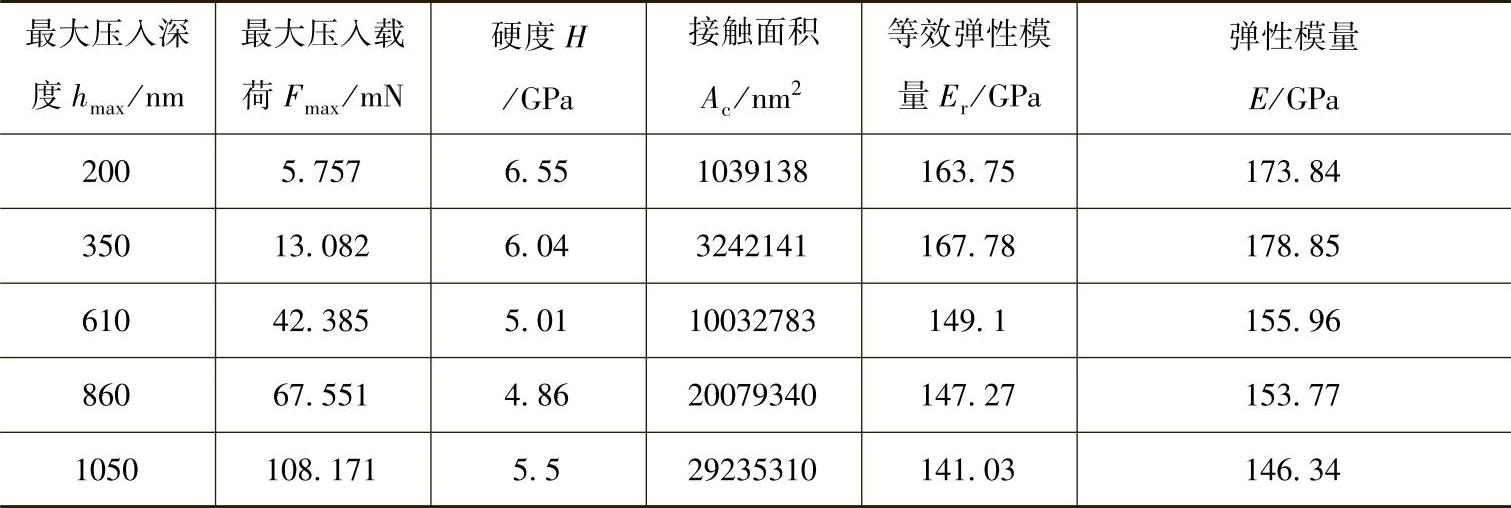
表4-9 2号500℃退火熔覆层不同压痕深度时的残余应力^[6]

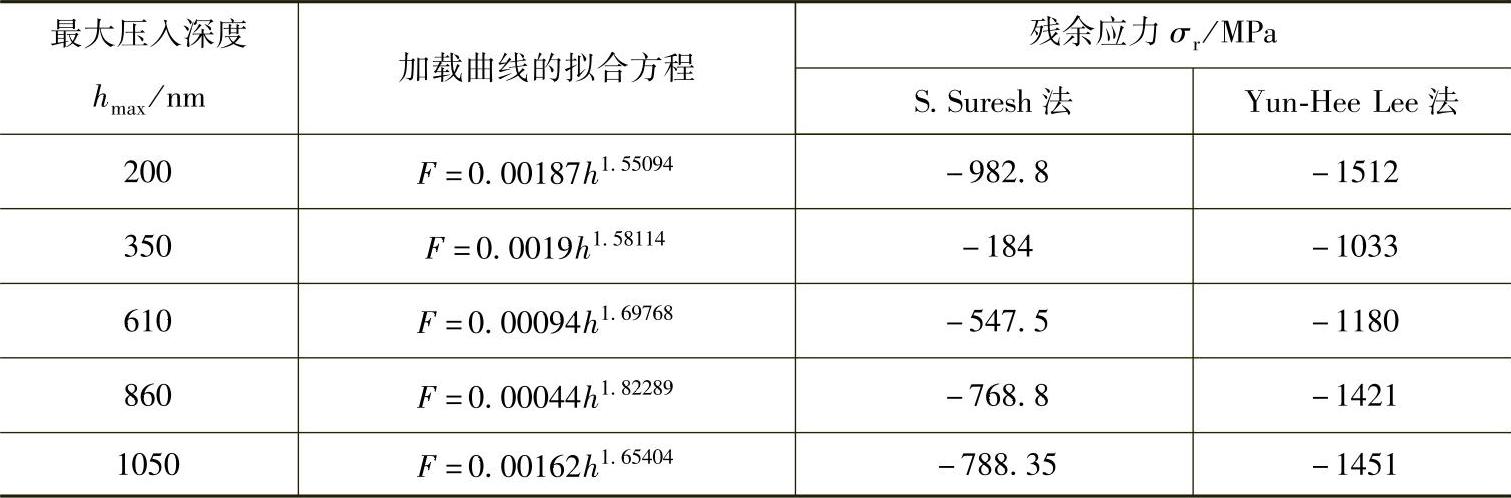
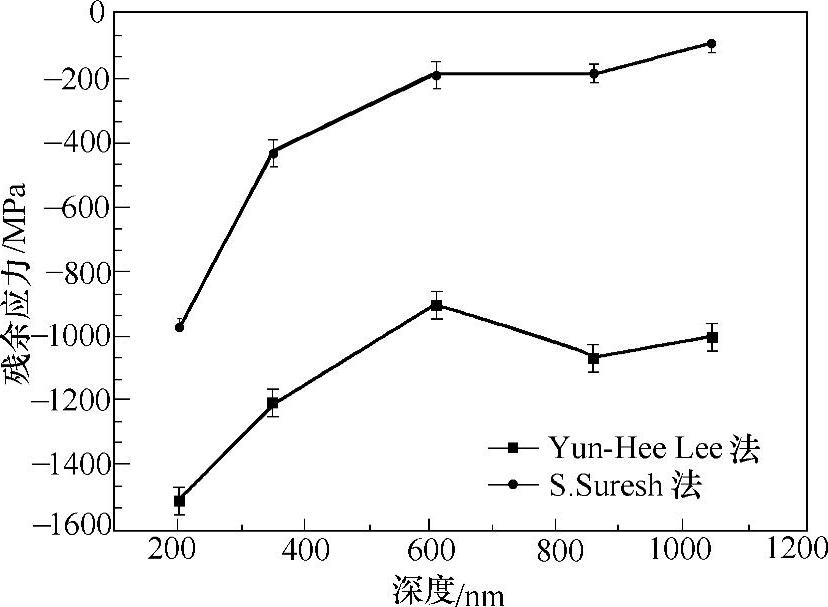
图4-11 不同压痕模型计算1号未处理熔覆层残余应力随压痕深度的变化^[6]

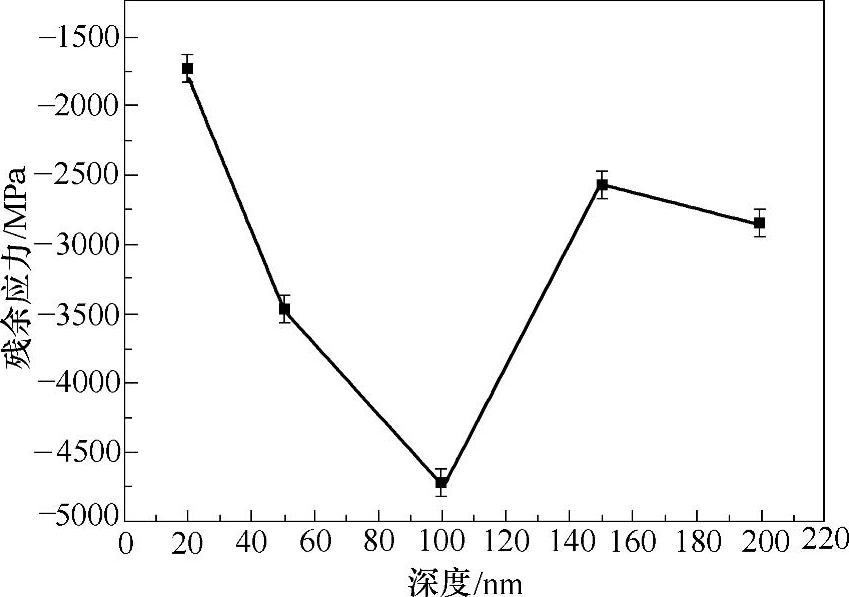
图4-12 S.Suresh模型计算1号未处理熔覆层残余应力随载荷的变化^[6]

利用X射线衍射法对Fe314涂层的残余应力进行了辅助测量，测量了微弧等离子熔覆Fe314涂层及不同退火处理后涂层的表面残余应力，结果如图4-14所示。等离子熔覆Fe314涂层的表面呈压应力，应力值约为（-544±20）MPa。经过500℃退火后，残余应力没有下降，反而略有上升。这是因为在此退火温度处理后，涂层发生了二次硬化现象，新产生的残余应力，使得整体的残余应力较原始熔覆层增加。另外，随着退火温度的继续上升，涂层的残余应力明显降低，600℃退火后涂层的残余应力最小。

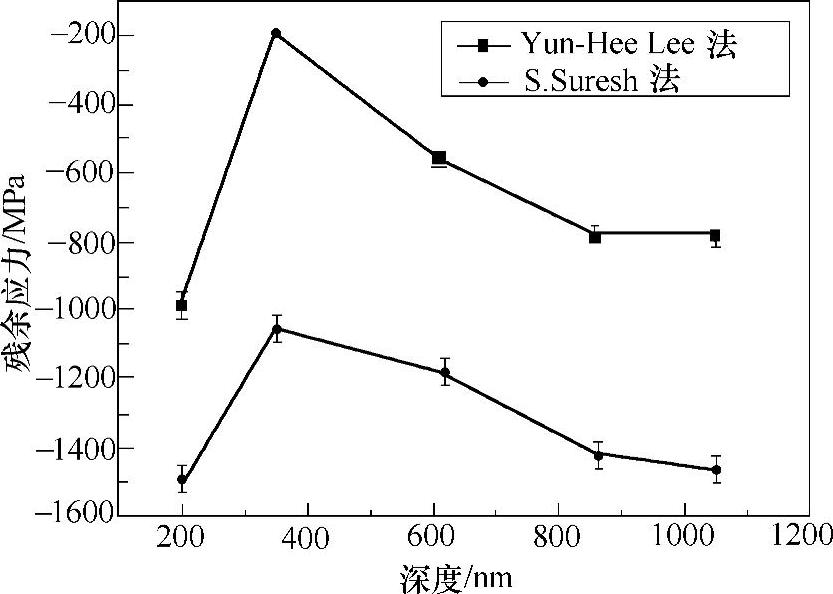
图4-13 不同压痕模型计算2号500℃退火熔覆层残余应力随压痕深度的变化^[6]

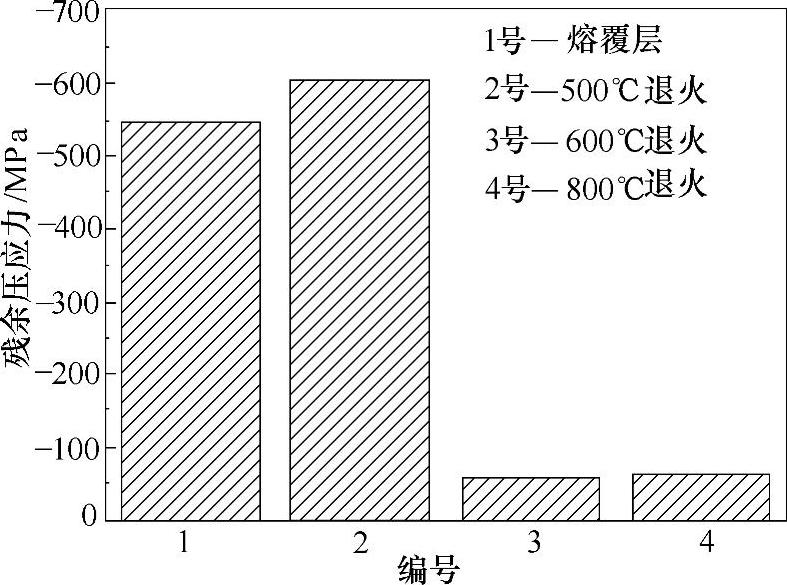
图4-14 X射线衍射法测量的不同温度退火Fe314涂层残余压应力^[6]

从图4-11可以看出，与X射线衍射法得到的测量结果一致，原始熔覆层整体呈现压应力。无论使用哪种模型计算，都发现表面处（压痕最浅200nm处）的压应力最大，这可能是由于试样制备过程中打磨抛光等过程对表面施加压力的结果。另外，两种模型计算的残余应力沿压痕深度的变化趋势基本一致，即随着压痕深度的增加，残余压应力减小并逐渐趋向平衡。还可以发现，使用Yun-Hee Lee模型计算的残余应力要远大于使用S.Suresh模型计算的结果，使用S.Suresh方法计算的结果在数值大小上更趋近于X射线衍射法得到的结果。

图4-12给出了1号未处理熔覆层残余应力随载荷的变化情况。使用S.Suresh模型中的固定载荷法测量得到的1号未处理熔覆层残余应力随载荷的变化情况，涂层内部的残余压应力随着载荷的增加迅速增加，在100mN左右处达到最大值，随后逐渐减小并趋于平衡。可以发现，该结果与图4-11的结果呈现较大差异，同时与X射线衍射法的测量差距也较大，故可以推断在使用S.Suresh压痕模型计算残余应力时，选择固定载荷法能更加准确地反应出材料的真实残余应力变化情况。

从图4-13可以看到，与1号未处理熔覆层的测量结果类似，500℃退火后涂层整体仍呈现压应力，同时，最大压应力仍然存在于表面处。这说明涂层的制备方法对涂层残余应力的测量有着不可忽视的影响。另外与图4-11不同的是，对于500℃退火涂层，随着压痕深度的增加，涂层的残余压应力增加，当压痕深度达到800nm后涂层的残余压应力趋于稳定。同时可以发现，使用Yun-Hee Lee模型测量的结果仍明显大于使用S.Suresh模型计算的结果。这说明造成这种差距的原因不在于涂层材料的变化，而在于模型本身的不同。具体来说，可能归结于模型过程中假设条件的建立，S.Suresh模型中假设卸载过程中的力不变，而Yun-Hee Lee则假设为线性卸载过程。

6.复合电刷镀n-Al₂O₃/Ni涂层的残余应力测量

使用纳米压痕仪XP系统对复合电刷镀n-Al₂O₃/Ni涂层（包括1号未处理、2号400℃退火）进行了固定压痕深度分别为100nm、150nm、200nm、250nm、300nm的压痕试验。将2号经过400℃退火的试样作为无应力状态样品，基于S.Suresh和Yun-Hee Lee模型进行残余应力的计算。

使用S.Suresh模型及Yun-Hee Lee模型进行固定压痕深度的残余应力计算得到的结果如表4-10、表4-11所示。

表4-10 400℃退火复合电刷镀n-Al₂O₃/Ni涂层不同压痕深度的残余应力^[6]

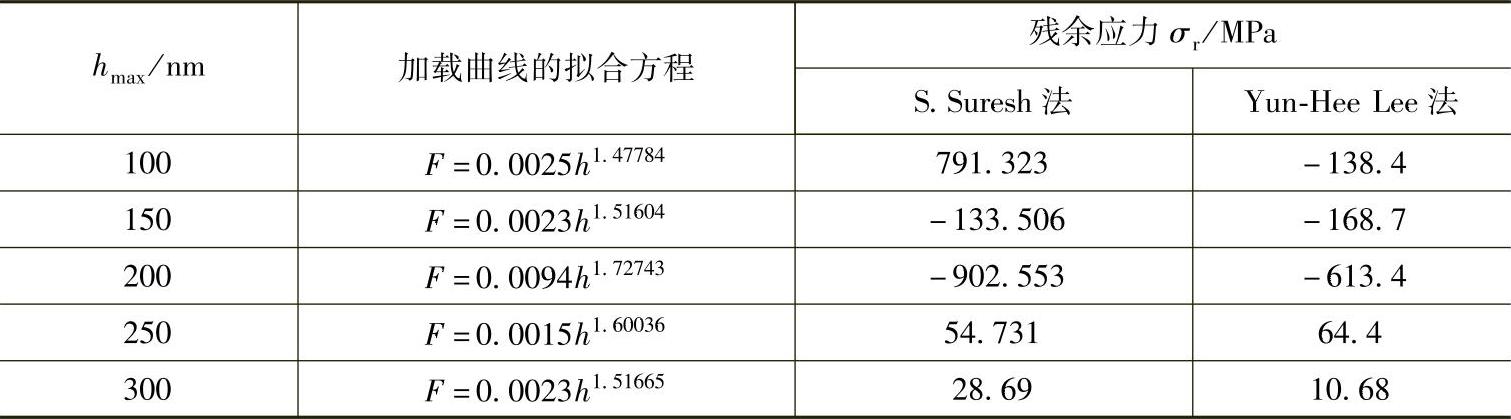
表4-11 复合电刷镀n-Al₂O₃/Ni涂层不同压痕深度时的力学性能^[6]

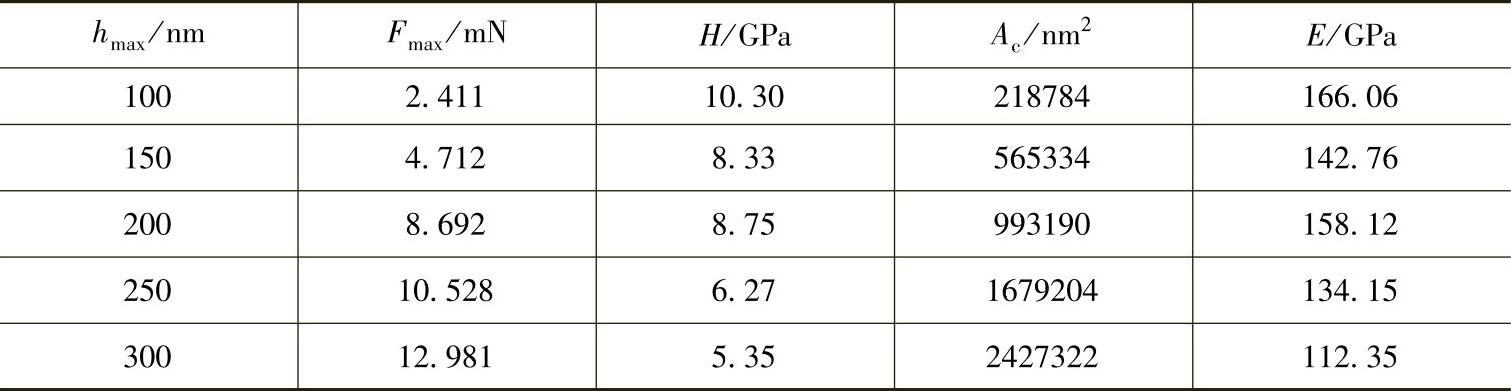
图4-15所示为X射线衍射法测量的退火前后复合电刷镀n-Al₂O₃/Ni涂层残余压应力。复合电刷镀n-Al₂O₃/Ni涂层残余应力约为（-710±26）MPa，经400℃退火后，残余应力值减小为（-79±6）MPa。这说明400℃的退火处理可以使复合电刷镀n-Al₂O₃/Ni涂层内部的残余应力明显减小，同时证明，在使用压痕模型计算涂层残余应力时，选用400℃退火后的刷镀层作为无应力对照组涂层是合适的。

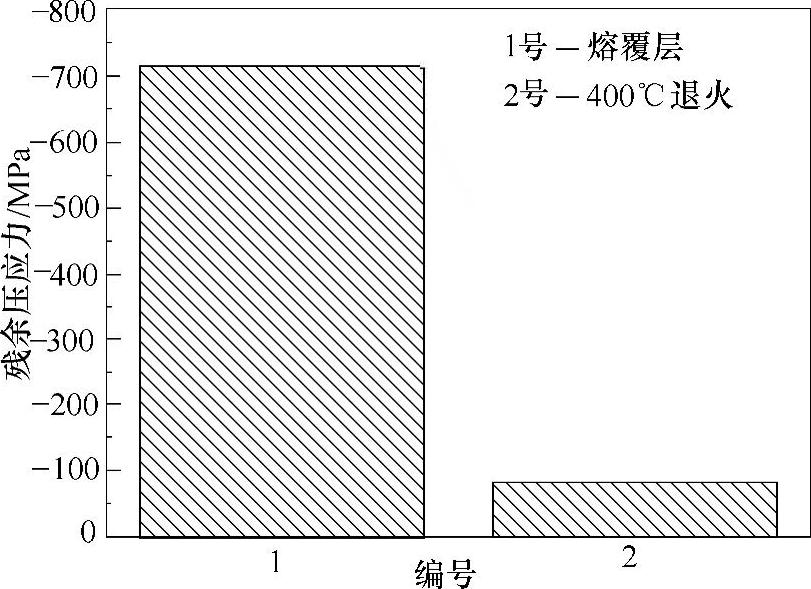
图4-15 X射线衍射法测量的退火前后复合电刷镀n-Al₂O₃/Ni涂层残余压应力^[6]

根据表4-10和表4-11得到不同压痕模型测得的复合电刷镀n-Al₂O₃/Ni涂层残余应力随压痕深度的变化，如图4-16所示。两种模型计算的残余应力仅在涂层表面压痕较浅处有较大区别，随着压痕深度的增加，残余压应力增加，在200nm处应力达到最大值。根据刷镀层的强化机理可以推断，该深度处微缺陷聚集，阻碍了位错的移动，导致该深度处的硬度值出现明显上升。当压痕深度超过200nm后，残余压应力逐渐转变为拉应力，并且趋于稳定。考虑到在压痕试验涂层的制备过程中，由于刷镀层的表面粗糙度较大，所以需要进行砂纸打磨和抛光处理。这一过程会对涂层表面施加一定的压力，很可能导致压应力的产生。从这个角度考虑，Yun-Hee Lee模型的结果更符合实际情况。另外，两类模型计算的刷镀层200nm附近的残余应力与X射线衍射法测得的残余应力都较为接近。

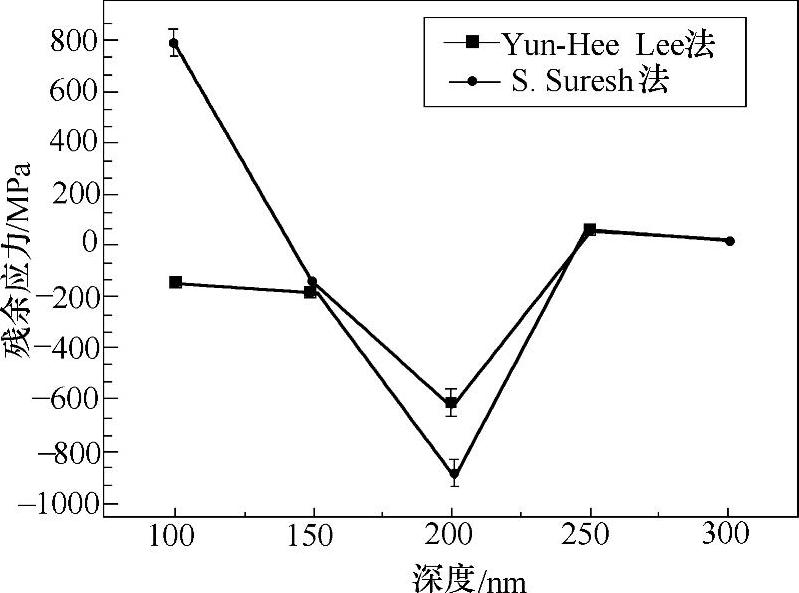
图4-16 不同压痕模型测得的复合电刷镀n-Al₂O₃/Ni涂层残余应力随压痕深度的变化^[6]