定峰方法及其他数据处理方法

在进行应力测量时需要定峰，即确定出衍射强度与衍射角关系图中的峰值位置，从而确定衍射线角位置2θ的数值，并计算应力^[37]。目前最常用的定峰方法有半高宽法、抛物线法、重心法，以及确定峰位差的交相关法。用何种方法定峰直接关系着峰值的准确度，定峰之前还要进行背底处理和强度因子校正等。

1.背底处理^[38]

衍射峰的背底是一些与测量所用的布拉格衍射无关的因素造成的，其中包括康普顿散射、漫散射和荧光辐射等。这些因素都受吸收的影响，有的强度还随sinθ/λ值的增大而增大。因此，扣除背底是提高定峰和应力测量准确性的必要步骤之一。

大量的研究表明，背底是一条起伏平缓的曲线，可以用一个三元一次方程进行描述。一般都倾向于把它当做一条直线，实践证明，这样的近似处理对于现行的测量准确度要求来说是可行的。为了扣除背底，首先要合理地选取扫描起始角和终止角，使衍射曲线的两端都出现一段背底。通常扣除背底的做法是：在曲线的前后背底上，从两个端点开始，分别连续地取若干个点（不少于5个），将这些点按最小二乘法拟合成一条直线作为整条衍射曲线的背底；然后将所测得的衍射峰各点的计数减去该点对应的背底强度，即得到一条无背底的衍射曲线，如图2-36所示。

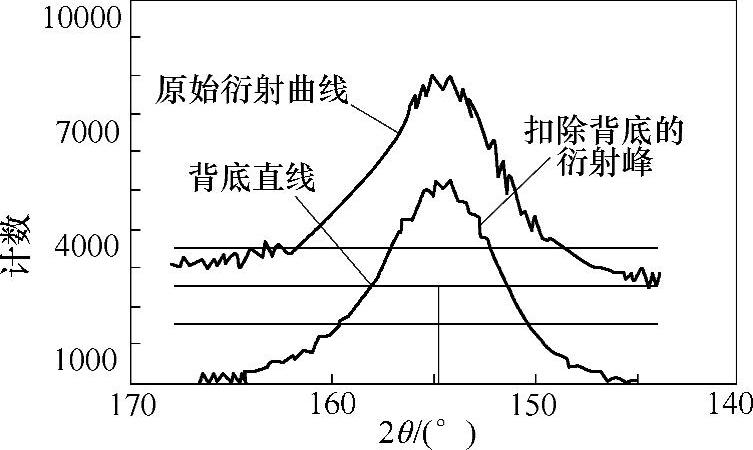
图2-36 背底处理及半高宽法定峰^[38]

2.强度因子校正^[38]

根据X射线衍射强度理论，与接收角2θ及Ψ角有关的强度因子包括洛伦兹-偏振因子LP（2θ）、吸收因子A（2θ，Ψ）、原子散射因数f（sinθ/λ）和温度因子e^-2D等。为了正确求得衍射角2θ，需要对强度因子进行校正，这同样也是提高定峰和应力测定准确性的必要步骤。经计算，在应力测量用到的2θ范围以内，原子散射因数和温度因子随2θ的变化很微小，可以忽略不计；而洛伦兹-偏振因子LP（2θ）尽管影响峰位，却与Ψ无关，在应力测量中也可以不加考虑；这样，最主要的就是吸收因子A（2θ，Ψ）。因此，在使用同倾法时计算程序中要加入吸收因子校正。若吸收因子恒等于1，就无需校正了。

3.半高宽法定峰^[38]

半高宽法是把衍射线峰强度1/2处的峰宽度的中点所对应的2θ值作为该衍射线的角位置，即衍射线半高宽中点的2θ值。一般计算软件所依据的数学模型如图2-36所示。把净峰高的两个峰腰部分当做直线，并用最小二乘法对实测点进行拟合；在净峰值强度1/2处作平行于横坐标的半高线与这两条峰腰直线相交；然后在两个交点之间取中点，这个中点的横坐标值即是所求的峰位。上述的峰值强度也非随机的最大值，而是峰顶拟合抛物线顶点的高度，这样可以减小随机误差。这种方法利用衍射曲线斜率较大的峰腰段进行计算，在这两段里，衍射强度的随机波动对峰位的影响较小，所以定峰精度较高。但它要求设定足够宽的扫描范围，以保证得到曲线的前后背底。

4.抛物线法定峰^[38]

抛物线法是把衍射峰顶部（峰值强度80%以上）的点，用最小二乘法拟合成一条抛物线，以抛物线顶点的横坐标值作为峰位的定峰方法，如图2-37所示。这种方法利用峰顶部分进行计算，所以如果对被测材料的衍射曲线形态比较熟悉，则有可能缩小扫描范围，从而缩短测量时间。具体的做法是：首先选定充分的扫描范围测试一次求出背底，作为公用背底，用于同一试样其他点或同种材质同样状态的其他试样的背底处理。随后的测试可以大幅度地缩小扫描范围，只要能保证得到各个Ψ角衍射峰的峰值80%以上部分，就能正确进行定峰。当然应当注意保持X射线管高压和管流的一致性，选用的入射准直管也应当是一样的。

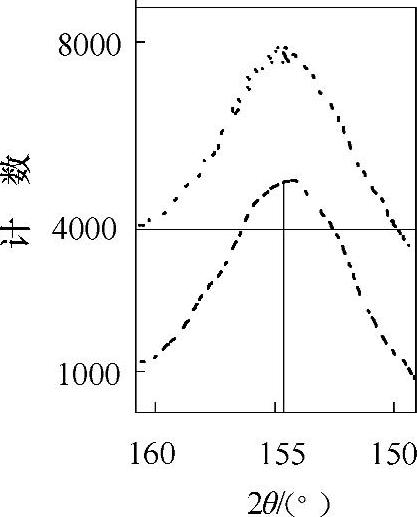
图2-37 抛物线法定峰^[38]

5.重心法定峰^[38]

重心法本来是以背底线以上整个衍射线所包围的面积的重心所对应的2θ作为峰位的定峰方法，物理概念很清晰，测试数据的利用率也很高。但是，实际应用效果并不理想，其原因在于峰两侧尾部的计数波动，虽然此处净强度不大，但是由于距重心较远，即杠杆臂较长，计算时对重心会造成一定的影响。如果截取净衍射峰峰值20%～80%之间的部分，将之看为一个封闭的几何图形，如图2-38所示，求出这个几何图形的重心作为峰位，则能够显著改善重心法的定峰精度。

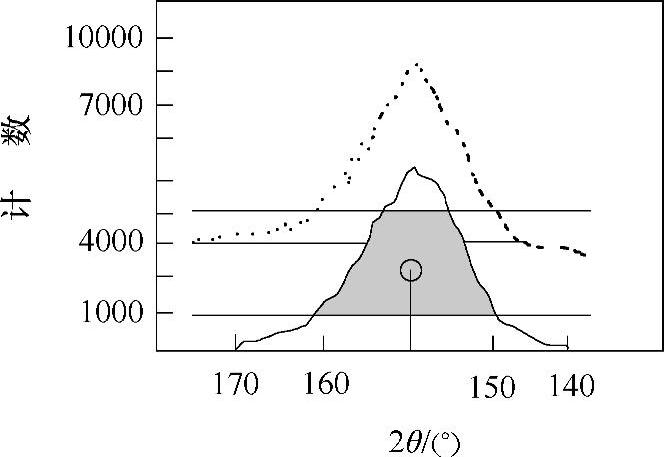
图2-38 重心法定峰^[38]

6.交相关法定峰^[38]

交相关法是20世纪80年代提出来的，该法可以计算出属于不同Ψ角的衍射峰之差，其原理公式为

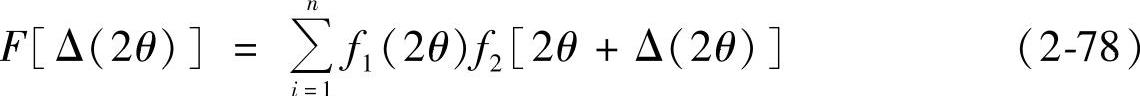
通过构造一个交相关函数F[Δ（2θ）]，使其每个函数值等于两条不同Ψ角曲线f₁（2θ）和f₂（2θ）上对应点的数值相乘再全部相加之和，其中f₂（2θ）的自变量要改变一个步距角Δ（2θ）。由式（2-78）可得，连续改变Δ（2θ）就能得到交相关函数分布曲线，然后利用最小二乘法对这个分布曲线的顶部进行二次拟合，便可求出峰位移。(www.xing528.com)

7.应力值的计算及误差分析^[38]

利用最小二乘法计算2θ对sin²ψ的斜率M，即

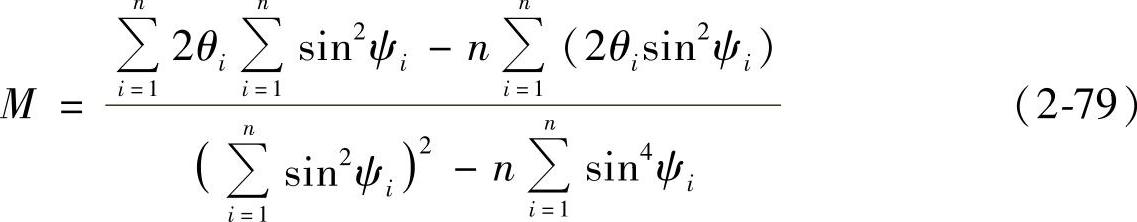
式中，n为测定应力选用Ψ角的数目。

为简化之，令：x_i=sin²ψ_i，y_i=2θ_i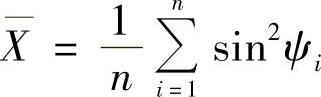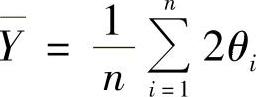，，，则式（2-79）可简化为

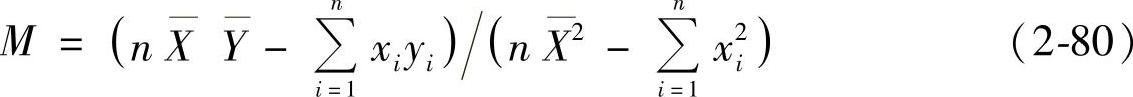
因此，2θ-sin²ψ的拟合直线可以表达为

y_i=A+Mx_i （2-81）

理论上，2θ和sin²ψ呈线性关系，然而测试所得的点与由它们拟合而成的直线之间总会有偏差，即存在一个拟合残差问题。应力误差Δσ即反映了拟合残差的大小，即

Δσ=KΔM （2-82）

式中，K为应力常数；ΔM为2θ-sin²ψ直线斜率的误差。

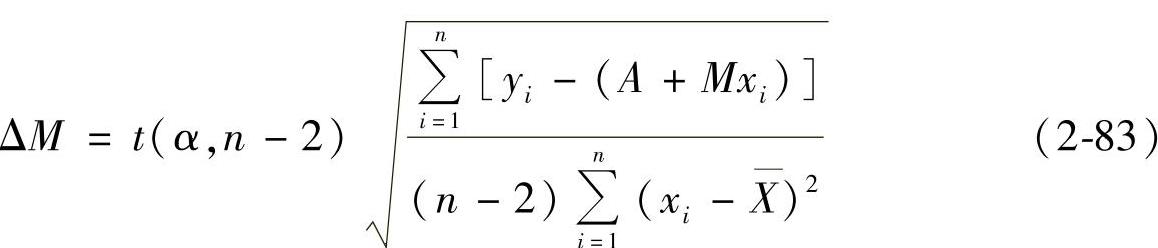
式中，t（α，n-2）为对应自由度（n-2）和可信度（1-α）的t分布值。

图2-39所示为三种实际测量结果，它们的误差大小各不相同，表现为以下两种情况。

1）在材料中无织构的情况下，Δσ是由各种随机因素造成的，是测量精度的表征。图2-39a的测量误差很小，图2-39b的误差则稍大。通常通过改善测量条件，还可以减小这种误差。随机误差的主要影响因素是衍射强度和衍射峰的半高宽。形象地讲，峰形敏锐，则误差小；反之，峰形漫散，则误差大。经过试验与分析，在连续扫描条件下衍射角误差Δ2θ与有关参数之间存在以下回归关系：

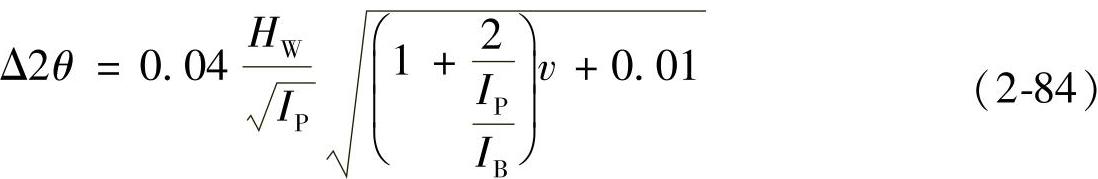
式中，H_W为衍射峰的半高宽；I_P为净峰强度；I_B为背底强度；v为计数管扫描速度。

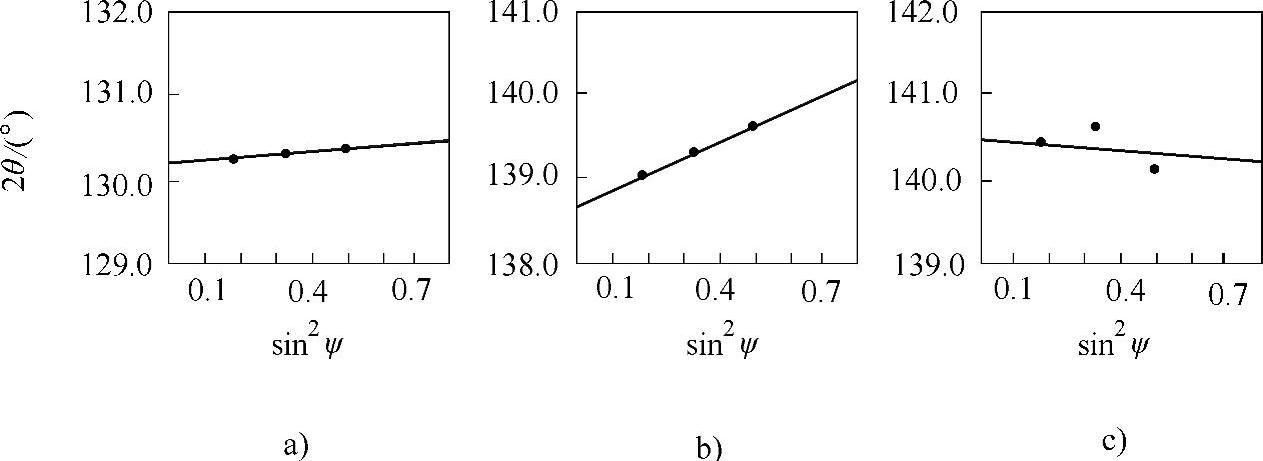
图2-39 应力值误差^[38]

a）Δσ很小 b）Δσ稍大 c）Δσ过大

2）对于图2-39c情况，2θ和sin²ψ不再是线性关系。因此，存在Δσ的原因除测量偶然误差以外，更主要的可能是存在织构或晶粒粗大。