测定原理和方法

1.二维残余应力的测定原理^[34]

X射线衍射法最早由前苏联学者Аксенов在1929年提出的。X射线应力测定的最基本的思路是，认为一定应力状态引起的晶格应变和按弹性理论求出的宏观应变是一致的，而晶格应变可以通过布拉格方程由X射线衍射技术测出，这样就可以从测得的晶格应变来推知残余应力。1961年德国学者E.Macherauch提出sin²ψ法，其逐渐成为X射线应力测定的标准方法。

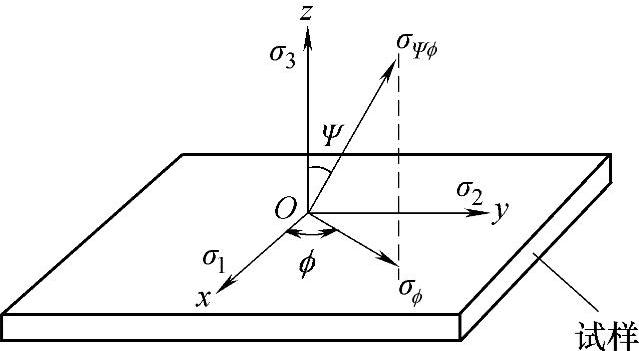
图2-31 σ_ψφ、σ_φ与主应力σ₁、σ₂、σ₃的关系^[36]

在一个确定的坐标系中，如图2-31所示^[36]，空间任意一个方向的正应力为

σ_ψφ=α²₁σ₁+α²₂σ₂+α²₃σ₃ （2-56）

式中，α₁、α₂、α₃为σ_ψφ对应的方向余弦，即

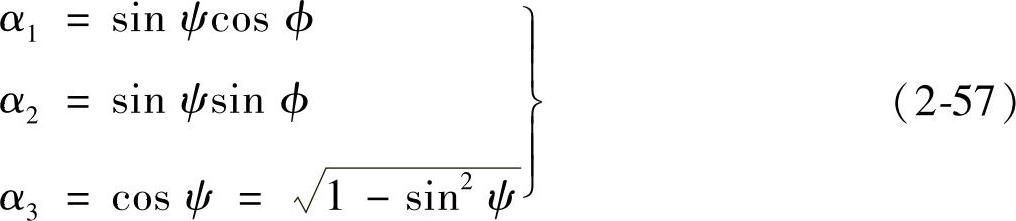
σ₁、σ₂、σ₃为主应力；φ和ψ分别为衍射晶面法线对选定坐标的旋转角和倾斜角。

同理，空间任意一个方向的正应变为

εψφ=α²₁ε₁+α²₂ε₂+α²₃ε₃ （2-58）

主应力与主应变两者关系的广义胡克定律为

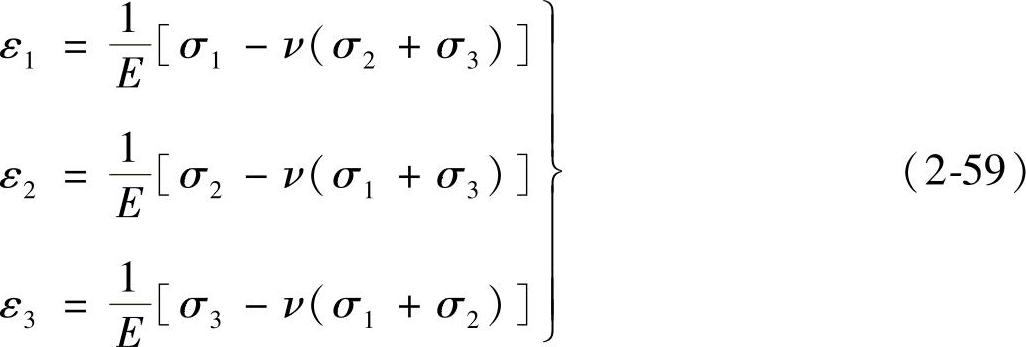
式中，E、ν分别是材料的弹性模量和泊松比。

由于σ₃=0，因而实际测得的应力是图2-31中的σ_φ，即试样（各向同性材料）的表面应力。

由布拉格方程2dsinθ=λ可以得出应变与衍射角位移的关系：

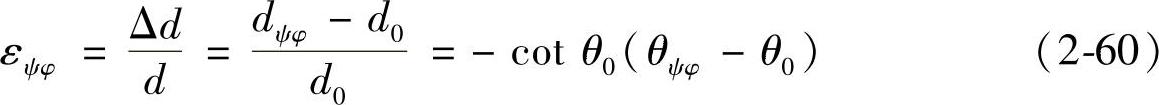
式中，d₀、θ₀分别为无应力时的晶面（hkl）的面间距和掠射角；d_ψφ、θ_ψφ分别为有应力时法向位于（ψ、φ）方向时的（hkl）晶面的面间距和掠射角；ε_ψφ是（ψ、φ）方向的应变。

由式（2-56）～式（2-60）可得

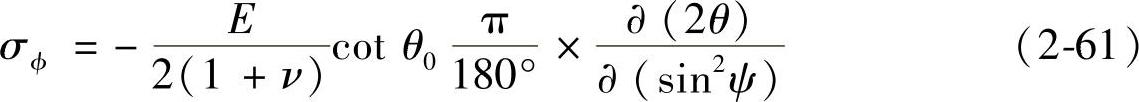
令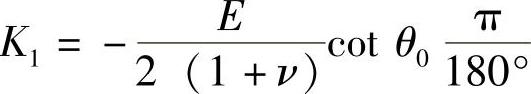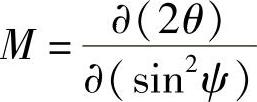，，则

σφ=K₁M （2-62）

式中，K₁为应力常数，M为2θ对sin²ψ的斜率。

式（2-62）即为测定残余应力的基本公式。

2.二维残余应力的测定方法

X射线应力仪是目前广泛使用的残余应力测试方法，大小试样均适用，且更适宜于现场测试。

X射线应力仪的核心部分为测角仪，装有可绕试样转动的X射线管和探测器。通过改变ψ使X射线管转动，以改变入射线的方向。目前，广泛使用的测角仪有两种，即Ω测角仪和Ψ测角仪，其衍射几何分别如图2-32a、b所示。

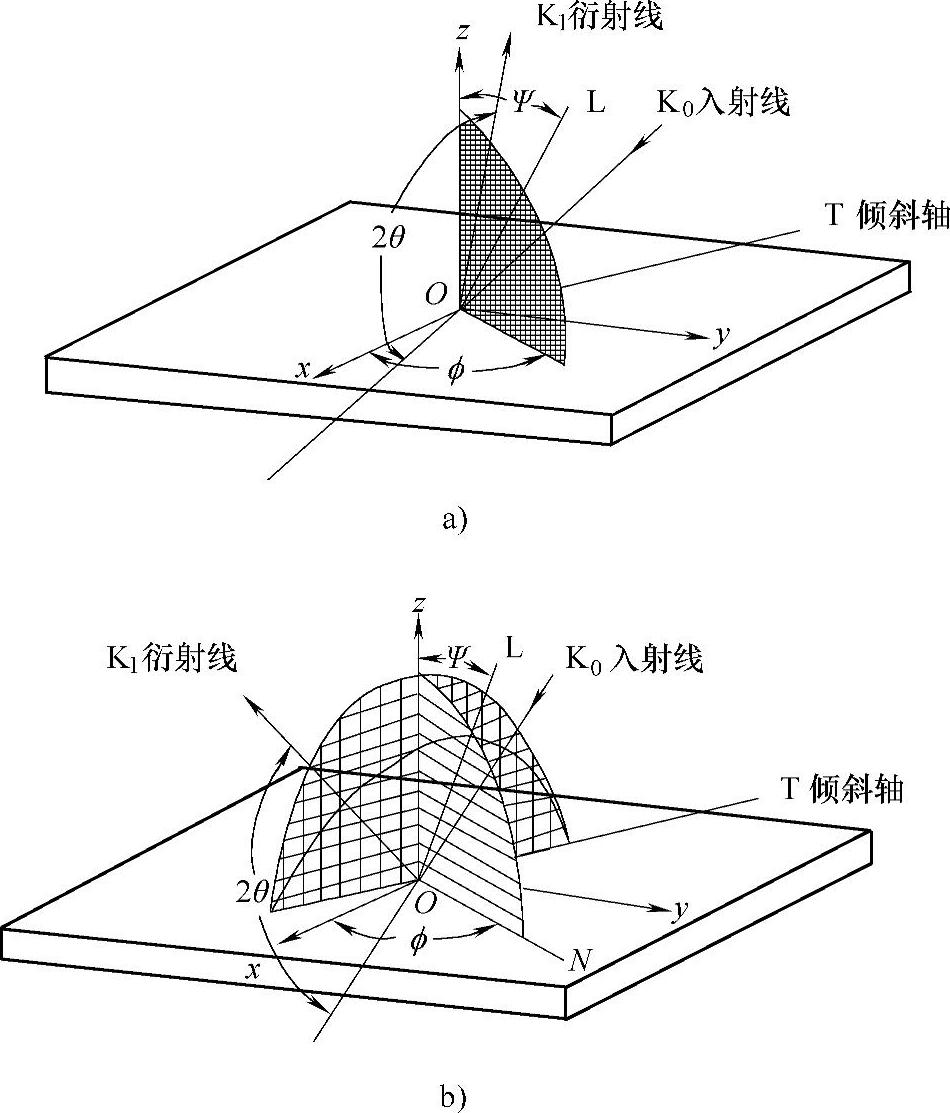
图2-32 Ω测角仪和Ψ测角仪的衍射几何^[36]

a）Ω测角仪 b）Ψ测角仪

（1）Ω测角仪 从式（2-62）中可以看出，只要测出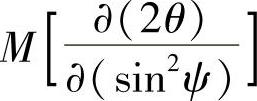，即可计算出应力。当以不同的角度ψ入射时，测出相应的2θ，用测定的2θ和sin²ψ做图，两者表现出图2-33所示的线性关系。求出直线的斜率M后，乘以已知的应力常数K₁，即可得出指定方向的应力σ_φ。ψ角所在的平面与试样表面的交线，就是所测应力的方向，常选ψ角为0°、15°、30°和45°。测出的2θ并非刚好位于一条直线上，此时可用最小二乘法进行数据处理。

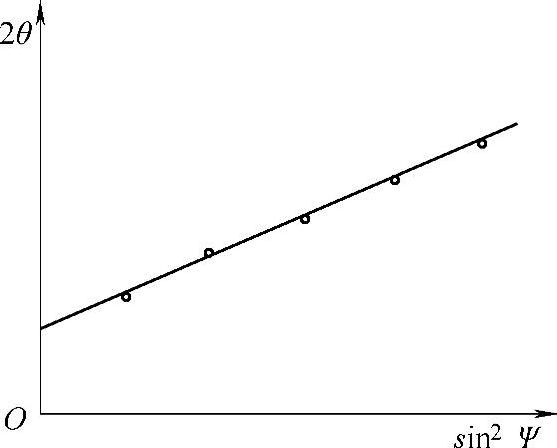
图2-33 2θ与sin²ψ的关系曲线^[35]

（2）Ψ测角仪 Ω测角仪和Ψ测角仪有很大区别，从图2-32中可以看出，在Ω测角仪中，ψ和2θ角在同一个平面内，即试样表面法线、衍射晶面法线、入射线、衍射线和待测应力方向共面。而在Ψ测角仪中，ψ和2θ角分别位于互相垂直的两平面内，此时试样表面法线、衍射晶面法线、待测应力方向三者共面，而入射线、衍射线和衍射晶面法线则位于另一平面。因此，为了测定ON方向的应力，必须测定法线位于NOZ平面内的晶面的2θ，此时入射线和衍射线都与OL呈90°-θ角。为了在不同的ψ角进行测定，应倾转T轴，即X射线管和探测器同步侧倾，应力计算公式仍为式（2-62）。与Ω测角仪相比，Ψ测角仪弥补了Ω测角仪在较大入射角度上探测不到衍射信息的缺点，可以在较大的倾角ψ下进行测量，因此适合于测定工件特殊部位（如齿轮根部、角焊缝处）的残余应力。

3.三维残余应力的测定原理及方法

随着复合材料越来越多的应用，各种表面改性技术的日益发展，材料表层往往处于三维应力状态。因此，三维残余应力的测定越来越受到关注。

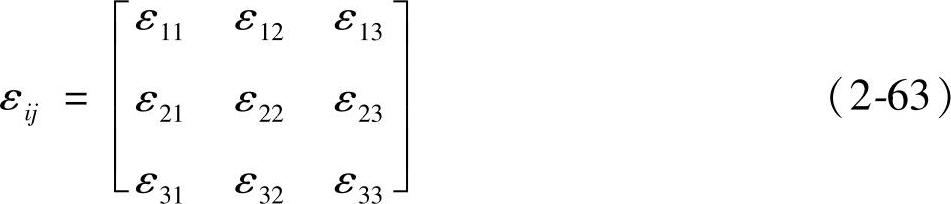
（1）X射线积分法 根据连续介质力学理论可知，在一受力作用的物体内，任一点的应变可用位于该点的一个小体积元的应变来描述，此体积元的应变可以用一个由二阶张量组成的应变矩阵来表示，即

(www.xing528.com)

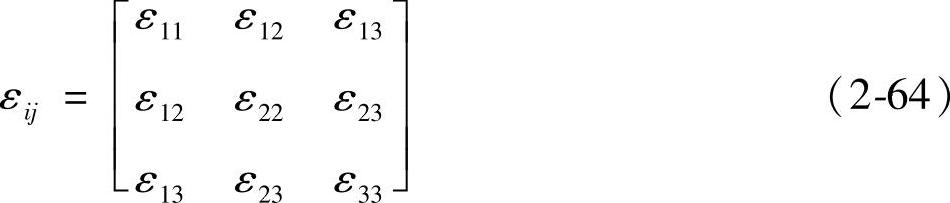
图2-34所示为该体积元的变形示意图及应变分量ε_ij，i代表产生应变的方向，j代表产生应变的面的法向。例如，ε₂₂表示x-z平面沿y方向的正应变，ε₁₃表示x-y平面沿x方向的切应变等。对于各向同性的材料，在平衡条件下，ε₁₂=ε₂₁，ε₁₃=ε₃₁，ε₂₃=ε₃₂，因此，式（2-63）中实际上只有6个独立分量，且以应变矩阵对角线为对称，即

同理，应力可以表示为

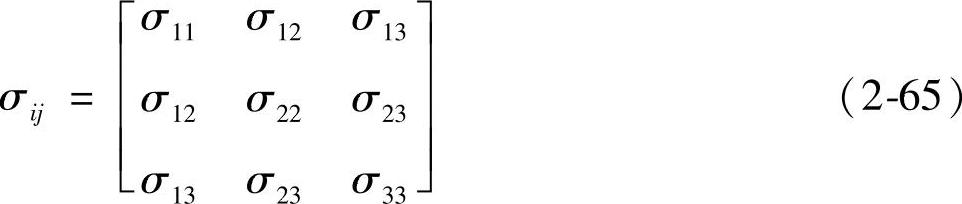
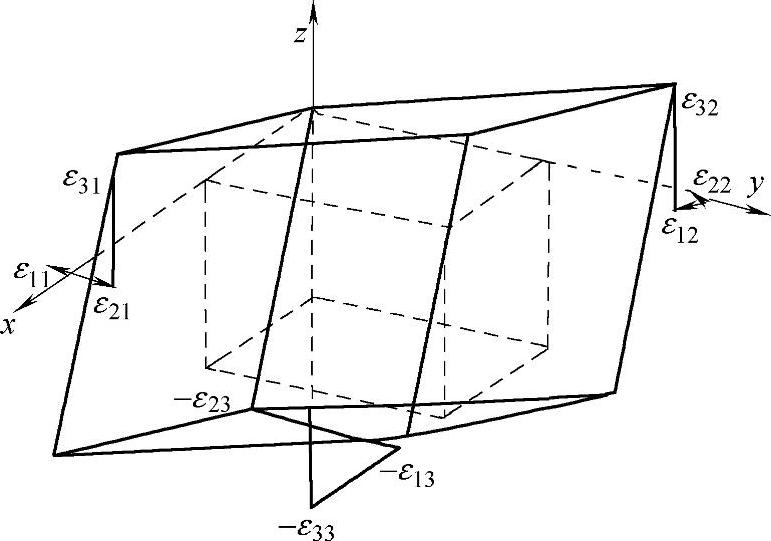
图2-34　体积元的变形示意图及应变分量[36]

在图2-34确定的坐标系中，使正应变ε₁₁、ε₂₂、ε₃₃与坐标轴一致，则任一方向的应变可以表示如下：

将式（2-57）代入式（2-66），可得：

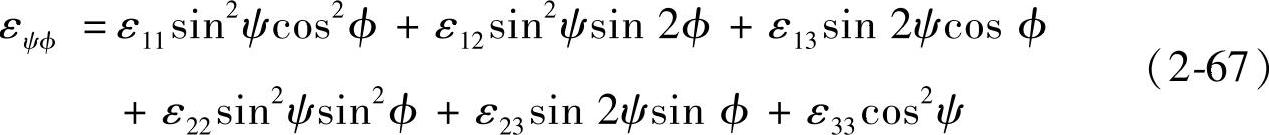
式（2-67）即为测定三维残余应力的基本公式，只要求出ε_ij，然后根据应力-应变关系即可求出σ_ij。

在实际的工件中，常常存在如图2-35所示的不均匀应力和应变，在深度比较小的范围内，可以认为深度z处的应变为

ε=ε₀+ε_zz （2-68）

式中，ε为深度z处的应变；ε₀为表面的应变；ε_z为应变梯度。

用于测定应力的X射线束具有一定的宽度和穿透深度，探测器采集到的是工件被照体积范围内的信息，探测到的应变是被照体积应变的加权平均<ε>，其数学表达式为

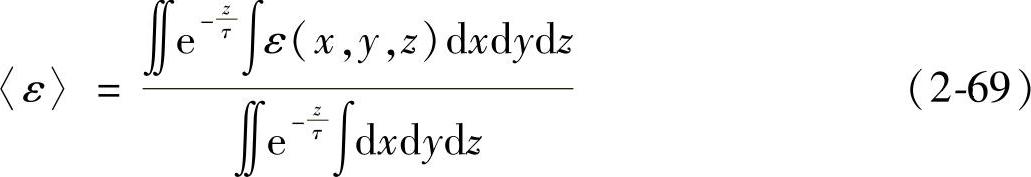
式中，τ为X射线在被测工件中的穿透深度；ε（x，y，z）是某一点（x，y，z）处的应变。求出ε（x，y，z）后，则即可求出该点（x，y，z）处的残余应变或残余应力及其在工件中的分布。

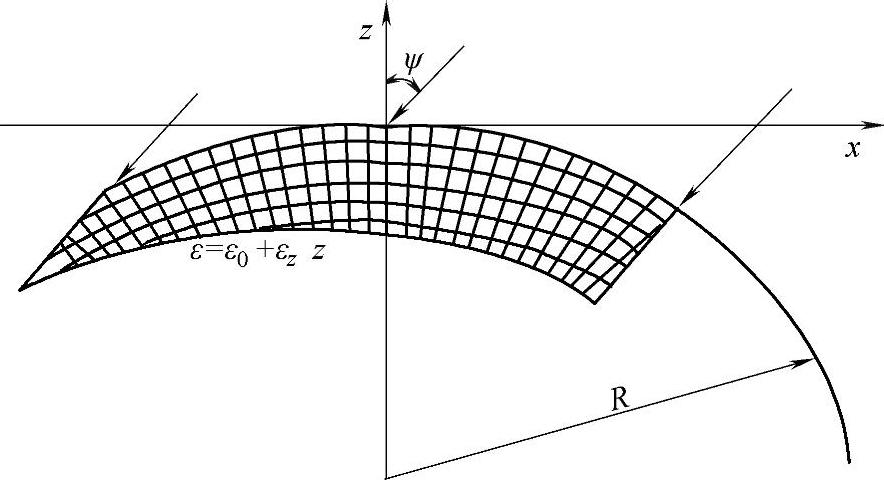
图2-35 工件存在不均匀应变示意图^[36]

为求解（x，y，z），可将式（2-69）中的ε（x，y，z）与式（2-64）的应变矩阵ε_ij联系起来。通过数学处理将ε_ij在工件深度z方向上按泰勒级数展开，当X射线有效穿透深度较小时，可以认为深度与应力变化呈线性关系。因此，泰勒级数展开式只保留到一次项，即

同理，应力可以表示为：

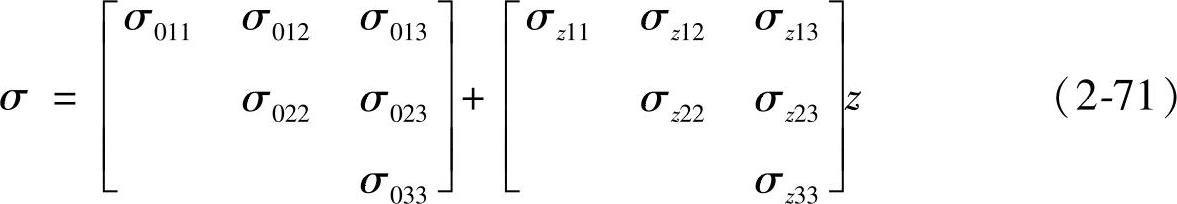
式中，ε_0ij和σ_0ij分别是被测工件表面的应变和应力；ε_zij和σ_zij分别是距离被测工件表面深度z处的应变梯度和应力梯度。将式（2-70）代入式（2-67）并与式（2-71）联立，求解应力的问题便转化为求解线性方程组的问题。从上述三式可以看出，该线性方程组共有12个未知量，因此，在无应力晶面间距d₀未知的情况下，至少要测出13组ψ、φ对应的d_ψφ，以求解线性方程组。计算出ε后，根据应力-应变关系即可求出σ。

（2）剥层法 剥层法应用较早，它是测定材料及其工件内部残余应力沿层深分布的方法。该方法通过切削或腐蚀使材料内部逐层露出，以测量各层的残余应力。这里所测得的残余应力并不等于剥层以前该处的应力，这是因为被剥除部分的残余应力的释放，将导致剩余部分的残余应力重新分布。对释放应力所造成的影响可以通过弹性理论的计算加以修正。例如，对圆筒试样用剥层法测定残余应力分布及其修正有如下的推导。

首先假定应力分布是轴对称的，沿轴向的分布也是均匀的，且在剥层的过程中，这种对称情况没有发生变化；其次假设剥除掉截面上的总应力，是以一个大小相等、方向相反的应力均匀地附加到剩下的截面上。设圆筒的内半径为a，外半径为b，从表面往里进行测量。当剥除到外半径为r时，用X射线法测得该处的轴向和切向残余应力分别为σ_lx和σ_tx，则该处原始的轴向、切向及径向残余应力σ_l、σ_t及σ_r可按式（2-72）～式（2-74）计算求得：

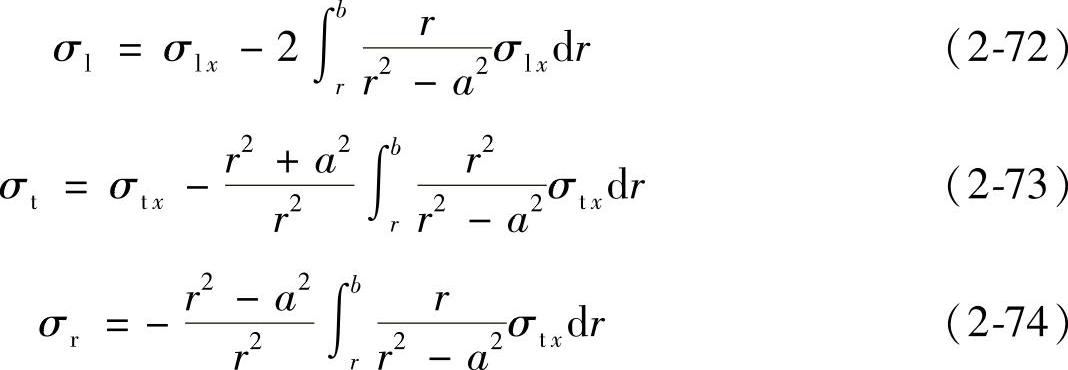
实际计算时，常采用图解法。以式（2-72）为例，在求出一系列与r对应的σ_lx后，分别以r和σ_lx/r为横坐标和纵坐标，由曲线下方对应的面积即可求出积分项数值，进而求出σ_l。

（3）多波长法 多波长法是利用不同特征X射线在材料中穿透深度的差异而获得不同深度的衍射信息，从而测定出不同深度的加权平均应力，据此推算出真实应力及其随深度的分布。

用此法对Ti-6Al-4V喷丸件的三维残余应力及其沿深度分布进行半定量分析计算。将X射线积分法中式（2-64）与待定的σ_ij（z）联系起来，将σ_ij按泰勒级数展开，并根据线弹性理论的边界条件、平衡条件和X射线衍射条件进行简化，进而用积分变换求解出应力状态标准方程，即

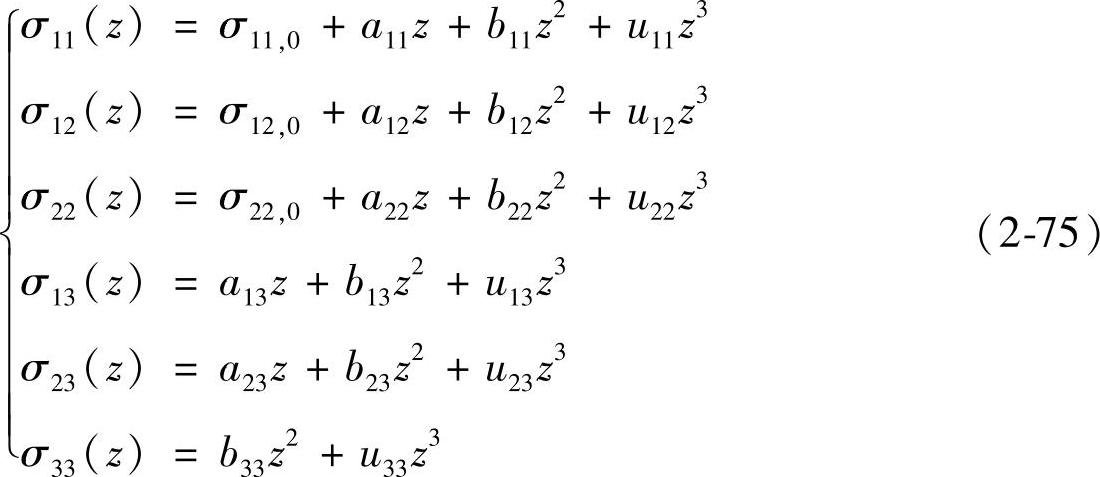
只要确定出式（2-75）中各项的系数，则问题即可得到解决。将式（2-69）改为用应力表示，并在X射线的有效穿透深度内积分，即

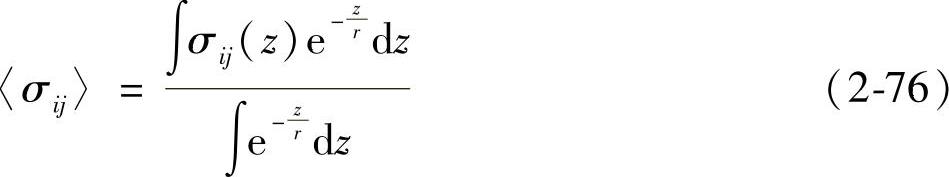
将式（2-75）代入式（2-76），经积分即可得

<σ_ij>=σ_0ij+a_ijτ+2b_ijτ²+6c_ijτ³ （2-77）

用三种不同的特征X射线照射试样，测出四个不同深度τ对应的<σ_ij>，即可求出系数a_ij、b_ij、c_ij，再代回到式（2-75）中，从而求出应力状态的标准方程。