纳米压痕技术的理论方法

1.Oliver和Pharr法

1992年，Oliver和Pharr提出了用纳米量级压痕的载荷-位移关系测试和分析材料力学性能的新方法，它是根据压痕过程中的加载和卸载曲线来研究材料的弹性模量。该方法是目前最广泛使用的方法，也是当前市场上主要的商业化纳米硬度计中所设置的计算方法，美国NANO仪器公司、Hysitron仪器公司及瑞士CSEM仪器公司生产的纳米硬度计均采用该方法。

金刚石压头压入材料表面的压痕深度随压入载荷的增加而单调增加，同时，在待测样品的弹性限度内，压头与材料表面的接触面积也随之增加。因此，在一个完整的加载-卸载周期中可获得所需的压痕数据，从而推导出硬度和弹性模量，如图2-1和图2-2所示。

图2-1 纳米压痕试验中载荷与压痕深度的关系

图2-2 材料表面及受压后的压痕示意图^[3]

按照经典的弹塑性变形理论中关于硬度和弹性模量的定义，被测试材料的硬度H和弹性模量E可分别由下式求出^[3]：

式中，F_max为最大压入载荷；A为压痕投影面积；S为卸载曲线上端部的斜率；E_r为当量弹性模量；E为被测材料的弹性模量；v为被测材料的泊松比；E_i为压头材料的弹性模量；ν_i为压头材料的泊松比。

由于该方法物理概念明确，计算简便易行，因而被目前广泛使用的商业化纳米硬度计所采用。

2.应变梯度塑性理论^[4]

Toupin在1962年首先提出应变梯度理论。Fleck等人在1976年发现，当尺寸很小的构件受到弯矩和扭矩作用时，随着构件尺寸的减小，其尺寸效应明显增大，并根据位错理论发展了一种宏观的应变梯度塑性理论。位错理论表明，材料的塑性硬化来源于统计储存位错和几何必需位错，它们分别与材料的塑性应变和塑性应变梯度相关。随后，有人基于该理论提出了一种新的模型，将宏观应变梯度塑性理论中材料本征长度l与材料的微观结构联系起来。该模型的结果表明，随着压入深度的减小，材料的硬度H呈增大的趋势。例如（111）单晶铜的压痕试验（见图2-3），它是用玻氏金刚石压头在单晶铜上得到了材料硬度随压入深度的变化关系，该结果与应变梯度塑性理论得到的计算结果非常吻合。但是需要注意的是，应变梯度塑性理论仅适用于塑性晶体材料。(www.xing528.com)

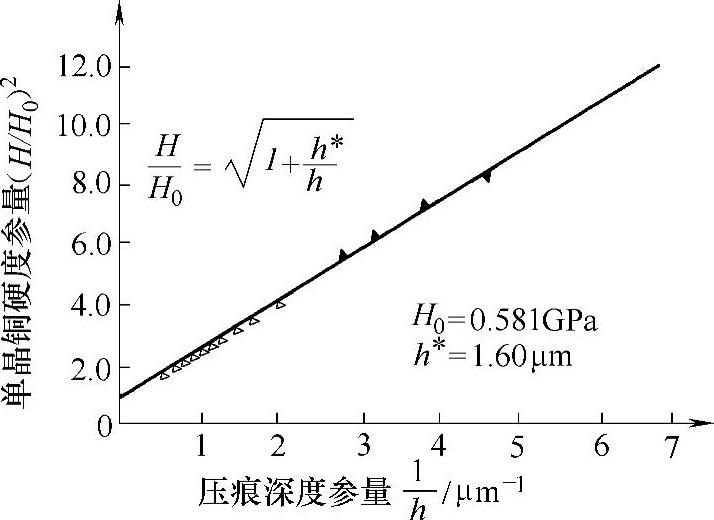
图2-3 单晶铜压痕试验中硬度与压痕深度的关系^[4]

注：H为材料的硬度；h为压入深度；H₀为与压痕尺寸无关的硬度；h^∗为表征硬度依赖尺寸的特征长度参数。

3.Hainsworth法^[4]

对于一些超硬材料（如DLC膜），在试验中无法得到理想的卸载曲线，因此无法用Oliver和Pharr法计算出合理的硬度和弹性模量。Hainsworth^[5]通过对加载曲线的分析发现，载荷F可以表示为压入深度h的幂指数形式，即F=K_mh²，系数K_m与维氏压头的压痕半径a及通过量纲分析得到的弹性变形有关，因此可以表示为硬度H和弹性模量E的函数。当从纳米压痕试验中得到载荷与位移的关系时，在弹性模量E和硬度H两者知其一的情况下就可以求出另一个量。该方法的缺点是关于弹性变形和塑性变形的假设太过于简单，是基于大量试验的经验公式，虽然计算结果与试验值有较好的吻合，但缺乏坚实的理论基础。

4.体积比例法^[4]

对于薄膜/基体组合体系的硬度试验，目前还缺乏很好的理论计算方法。Sargent在1986年提出了用体积比例法来计算薄膜/基体组合体系的硬度H，可用下式来表示：

式中，H_f为薄膜的硬度；H_s为基体的硬度；V_f为薄膜的塑性变形体积；V_s为基体的塑性变形体积；V为塑性变形总体积。

由于在应用上存在薄膜和基体材料塑性变形体积难以准确测定的困难，因此该方法在实际中很少采用。薄膜/基体组合体系的力学性能研究是目前的研究热点，但多局限于试验研究方法，试验的结果也难以完全排除基体对薄膜力学性能的影响。

5.分子动力学模拟法^[4]

该方法在原子尺度上考虑每个原子上所受到的作用力、键合能及晶体的晶格常数，并用牛顿运动方程来模拟原子之间的相互作用，从而对纳米尺度上的压痕机理进行解释。由于原子间的作用关系十分复杂，有许多物理现象还无法用现有的理论来解释，因此模拟的结果还有待于进行试验验证。