观测器应用设计

观测器的设计主要有：被控对象建模、传感器建模和观测补偿器设计。本节结合伺服控制系统，具体地给出其中每一部分。

1.被控对象建模

通常被控对象具有如下形式：

式中 K——比例增益；

N——积分阶次；

G_LPF（S）——被控对象滤波作用的传递函数。

在伺服系统中，被控对象增益K是K_T/J，K_T是电动机转矩常数，J是电动机与负载的总转动惯量。负载转动惯量可能比电动机转动惯量大很多倍，在设计观测器时，总的被控对象增益实际上可能是未知的。标称增益通常必须通过实验来确定。对于增益变动的问题，属于另外一个内容，在正常情况下，如果变化大于20%，观测器的优势就很难实现。

电流乘以增益K，获得电动机的加速度，加速度积分一次，获得电动机速度，伺服系统具有一阶积分，即N=1。

伺服电动机的滤波作用存在于黏性阻尼和绕组间的电容。黏性阻尼对低于几赫的信号具有轻微的镇定作用，由于它在系统中几乎不起什么作用，通常被忽略。与绕组相连接的寄生电容具有重要的作用，但对控制系统的直接作用通常几乎没有，因为这种作用的频率范围远高于伺服控制器的带宽，因此通常也被忽略。

2.传感器建模(www.xing528.com)

建模的任务是必须确定传感器的传递函数，其关键参数是滤波参数和比例参数。伺服系统用增量编码器作为传感器，其传递函数为一阶积分，因此传感器建模就变成了一件微不足道的事情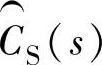，=G_S（s）。如果传感器是旋转变压器与正弦编码器，模型需要增加包括反馈信号变换引起的相位滞后，它通常取决于旋转变压器恢复位置信息所采用的方法。本节为方便说明，使用的估计传感器模型是以增量型传感器模型为基础建模的。

3.观测补偿器设计

观测补偿器设计就是选择补偿器中的增益的过程，它可归结为是P、I、D增益的不同组合。采用补偿器的目的是以足够的稳定裕度使观测器误差趋于零。任何用于镇定传统控制回路的方法都适合于观测器回路。在通常的伺服控制系统中，PID补偿器也许是可利用的最简单的一种补偿器。在设计补偿器时，PID补偿器已经足够了。

在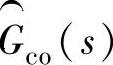的设计中，可以忽略饱和问题。控制器的PID设计要考虑到饱和问题，然而通常这个问题与观测器无关。由于它们跟随实际的被控对象，所以一般不受需要饱和限制条件的支配。因此，PID补偿器通常是不要求饱和限制的。

4.小结

图10-8是用于消除由简单差分引入的相位滞后的Luenberger观测器结构。在实体系统中，传感器使用增量型编码器，反馈电流I_F乘以K_T产生电磁转矩T_e，而I_F乘以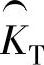产生电磁转矩的估计值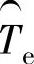。电磁转矩由电动机绕组产生，它同扰动转矩T_D相加，形成总转矩。总转矩除以转动惯量J，获得电动机加速度，加速度积分获得速度v_M，再一次积分，获得位置P_M。后一个积分被看做传感器的一部分，对于一个增量型编码器，反馈没有相位滞后，这种形式是合理的。观测器以数字形式实现，在模型系统中，积分1/S用数字等效形式Tz/（z-1）取代，因而模型系统与实体系统是相似的。

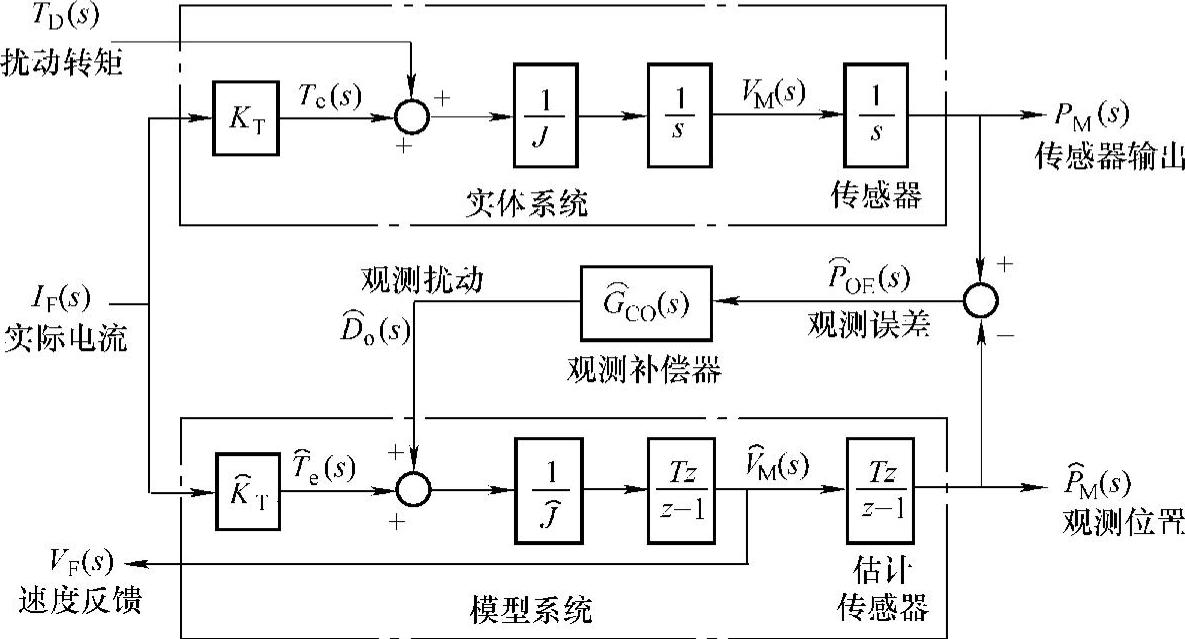
图10-8 Luenberger观测器结构

模型系统与实体系统的第二个积分都被看作传感器的一部分，而不是电动机的一部分。由于关心的是速度，因此观测器中观测速度（V_M是被控对象的输出反馈V_F，在这种情况下，观测器的目的是消除简单差分所带来的相位滞后。