观测器运行分析与优化

Luenberger观测器可以通过把它的结构表示成传递函数来分析，传递函数结构能够表征观测器的详细运行情况，有利于观测器的调试。

从图10-6可以看出，观测器传递函数有两个输入Pc（S）和Y（S），以及一个输出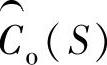。在分析中，把实际模型和传感器看作一个黑箱子，重点在于对观测器的输入与输出之间关系的理解，忽略观测器内部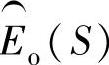和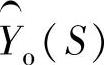。事实上，由于框图缩减为一个简单函数，这些信号是接触不到的。用Mason信号流图法建立观测器的传递函数，得到

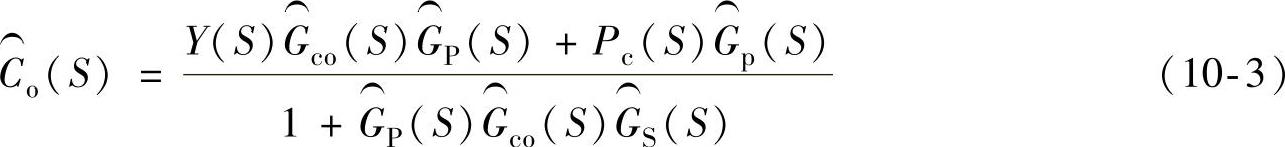
式（10-3）是两个因式之和，把这两个因式完全分离开，有

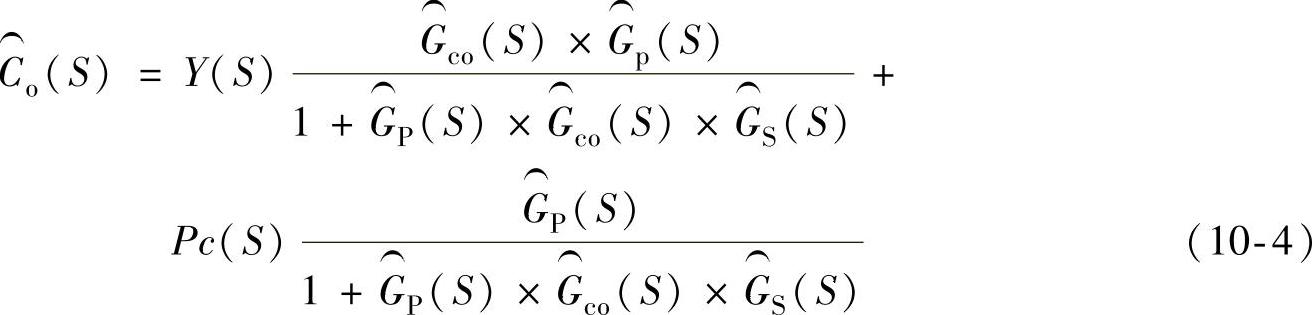
式（10-4）中第一个因式取决于传感器输出Y（s），改写后，得

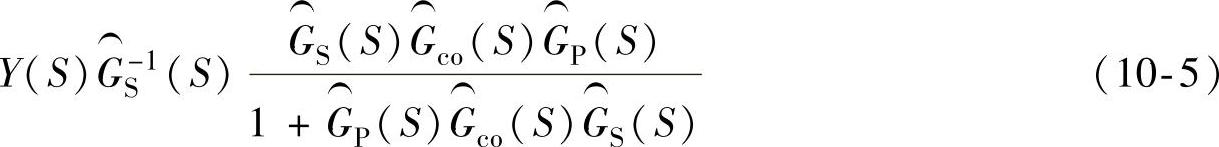
式（10-5）可以看做是系统输出乘以估计传感器逆的传递函数，然后由右边的一项滤波。由后面分析可知，右边的这一项是一个低通滤波器。因此，式（10-5）是图10-4中给出的形式后接了一个低通滤波器。

式（10-4）中，第二个因式取决于功率变换器输出Pc（S），改写后，得

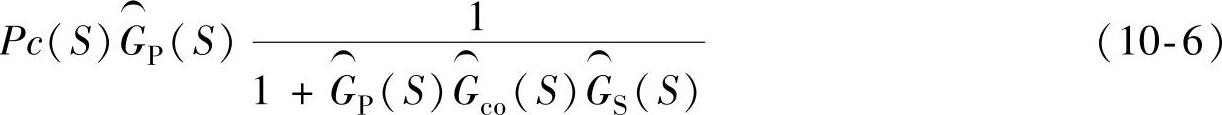
在式（10-6）里面，估计的被控对象传递函数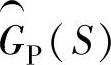被抽出来成为滤波器项的比例系数，比例系数项等效于图10-5中用来计算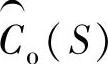的形式。由后面分析可知，右边的这一项是一个高通滤波器。因此，式（10-6）是图10-5中给出的形式后接了一个高通滤波器。(www.xing528.com)

下面来分析上面提到的这个低通滤波器和这个高通滤波器。式（10-5）中右边一项可以看作一个低通滤波器：

下面对式（10-7）中每一项进行分析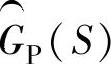：是被控对象模型，控制系统的被控对象通常至少会有个积分器，在高频段，这一项的幅值会衰减到接近零。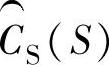是传感器模型，通常大多数传感器都包含低通滤波器，因此在高频段，这一项总是衰减的。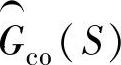是构建的，会满足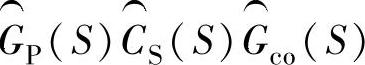的开环增益在观测器穿越频率处将有足够大的相位裕度。同实际控制回路一样，补偿器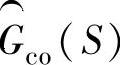具有足够高的微分阶次，以避免开环增益较高时出现的180°相位偏移，但是微分阶次又必须足够低，以满足增益在高频段衰减到零。因此，计算所得三项乘积在高频段数值小。在高频段幅值下降到很小，式中1在分母中占主导地位，于是，式（10-7）就被简化为它的分子，即幅值很小，接近为零。在低频段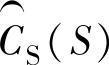，有一阶积分，这一项具有大的幅值。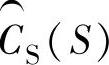是一个在低频段幅值为1的低通滤波器。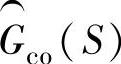将增加一阶积分，或至少会有一个比例项。计算所得三项乘积在低频段幅值大。在低频段幅值大，式中1在分母中可忽略，于是，式（10-7）就被简化为1。低频段的增益为1，高频段的增益接近零，这两个特征是低通滤波器的表征。

式（10-6）中右边一项可以看做一个高通滤波器，即

用类似推理得到，式（10-8）在高频段，分母衰减到接近1，使得式子简化为1。在低频段，分母非常大，使得这一项非常小。这种特性是高通滤波器的表征。

最后，把式（10-5）和式（10-6）合并起来，以框图的形式给出Luenberger观测器的滤波器形式，如图10-7所示。图中展示了观测器如何将输入Y（S）、Pc（S）相结合，产生观测状态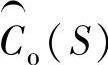的。Y（S）提供了良好的低频信息，但对噪声敏感，因此，在这一项后面接一个低通滤波器。Pc（S）项提供的低频信息很差，因为积分增益即便只有轻微的偏差也会受影响而产生漂移。另一方面，这一项不像Y（S）项那样容易产生高频噪声，因为被控对象正常情况下至少含有一个积分项，其作用如同滤波器，消除了通常存在于功率变换器输出中的噪声成分。因此，这样的一项后面因该跟随一个高通滤波器。

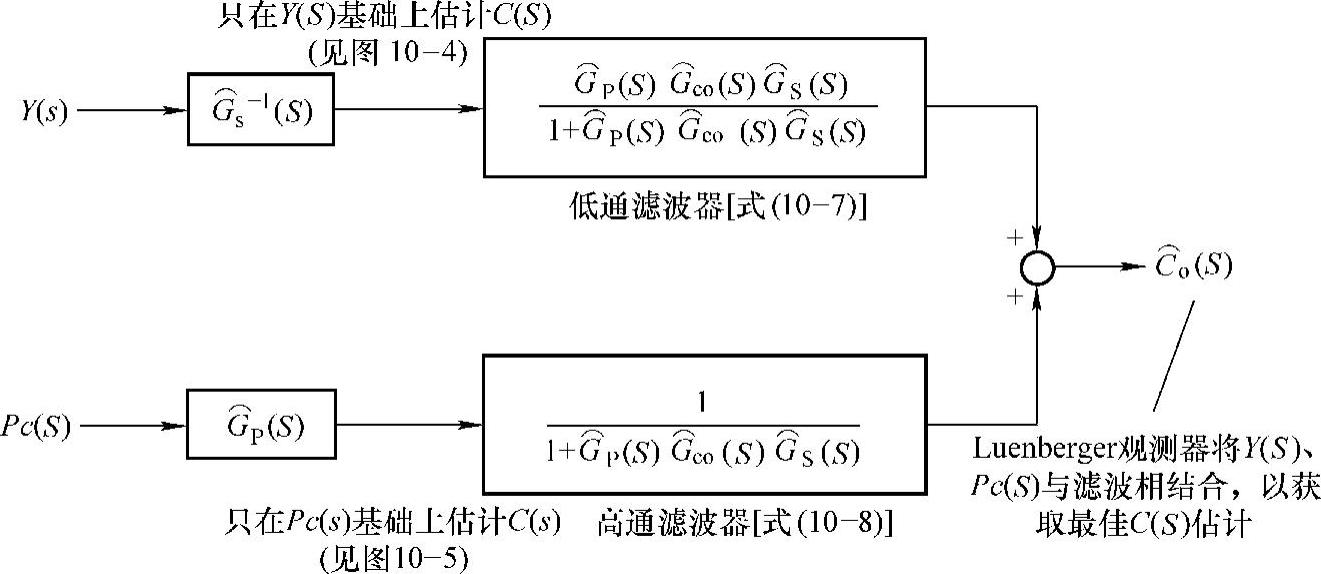
图10-7 Luenberger观测器的滤波器形式

Luenberger观测器用两种不同的方式从不同的两个信号源形成观测状态，并采用滤波将各自滤波器的最佳频率范围组合成一个输出。因此，观测器对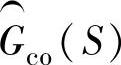、、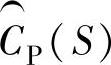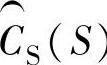调试的过程就变成了构造滤波器的过程，对于设计者来说，这样的过程会是比较熟悉的。