构建观测器的模型方法

图10-3所示是传统的控制系统，在理想情况下，控制回路采用实际状态C（S）作为反馈。但是，经传感器获取状态，传感器产生反馈变量Y（S）。理想的传感器定义为G_S理想（S）=1，输出Y（S）取代了实际状态C（S）。值得注意的是，传统控制系统把Y（S）取代C（S），忽略了G_S（S）≠1所带来的影响。传感器产生的典型问题是相位滞后、衰减和噪声。由传感器或者传感器的物理结构产生的相位滞后通常是回路不稳定的主要因素，传感器所带来的噪声通常需要在控制回路中增加滤波器来进行校正，从而又进一步增大了相位滞后，最终降低了稳定性裕度，这些不期望的因素都包含在G_S（S）中。

图10-3 传统控制系统

同用观测器相比，选择一种更快或者更准确的传感器，更加有预测性且更加容易实现，但是诸如价格、尺寸以及可靠性等因素限制了最好传感器的使用。因此，观测器的作用是充分用好传感器。使用Luenberger观测器可以将G_S（S）≠1所带来的影响最小化。

消除G_S（S）≠1所带来的影响，一般有两种方法。一种备选方法是在传感器信号之后紧跟一个逆向传感器传递函数，如图10-4所示。从理论上来说，这种方案是可行的，遗憾的是G_S（S）的性质使得求逆并不现实。G_S（S）通常是一个低通滤波器：

它的逆为

式（10-2）里面含有一个一阶微分，在大多数情况下，微分会产生过大的输出噪声而并不实用。

另一种避免G_S（S）≠1带来影响的备选方法是被控对象的仿真模型作为正在执行的控制回路，电力变流器的输出信号Pc（S）作用于与实际被控对象G_P（S）并行的被控对象估计模型，如图10-5所示。由图能够看出，这样的解决方案容易受漂移的影响，大多数控制系统的被控对象至少包含一个积分器，实际被控对象和模型之间的偏差会导致估计状态发生漂移，这种方案也是不实用的。(www.xing528.com)

图10-4 增加逆向传感器传递函数

图10-4所示的方案完全取决于传感器，它在低频段运行良好，但在高频段会产生很大的噪声。图10-5中的方案完全取决于模型与电力变流器的输出信号，在高频段运行良好，但是低频段会发生漂移。结合这两种方案最佳部分，继续构建Lu-enberger观测器，增扩图10-5的结构，运行并联的实际被控对象和传感器与估计被控对象及传感器，产生实际输出Y（S）和观测输出，如图10-6所示。

图10-5 从被控对象模型中获得被控状态

图10-6中，如果估计模型是实际对象的准确模型，这时或者。这种情况下，观测状态是实际状态的准确表示，因此可以用来对控制回路构成闭环，G_S（S）的相位滞后对系统不再起作用，也就是消除了G_S（S）的影响。在任何实际系统中，很多因素使得。观测器补偿器将误差返回到模型，使误差趋于零。通常是高增益的PI控制律或者PID控制律，高的增益会使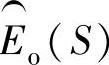最小化，观测状态就成了实际状态C（S）合理的表示。当然，它比传感器输出Y（S）准确得多。

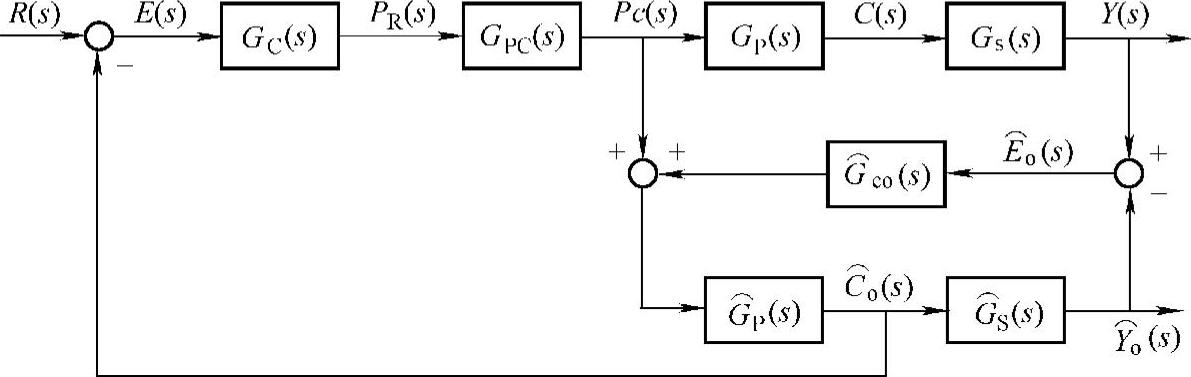
图10-6 基于Luenberger观测器的控制回路

Luenberger观测器的观测状态用来使控制回路形成闭环，它与图10-3所示的传统控制系统相比，传感器输出不再用来构成闭环，而是驱使观测器形成一个观测状态。用观测状态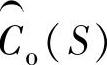构成的闭环回路，在一定频率范围内使得传感器的相位滞后与衰减得到消除。