基于双重卷积的实现方法

传统的S形曲线加减速方法的实现是比较困难的，它需要大量的计算，并且编程复杂。因此，本节将采用卷积的方法规划S形曲线加减速。在信号处理中，任何一个线性系统的输出都可以通过将输入信号与系统函数（系统的冲激响应）做卷积获得，其算法如下：

由式（9-41）可知，卷积可以起到滤波的作用，即卷积的流程需要保留滤波器冲激响应的时间次序，把它逐点乘以指定n开始的相应点x。把每次的乘积结果加在一起，获得滤波器的一个输出点y。然后把n的值加1，重复乘法和加法程序，获得y中下一个滤波的数据样点。卷积公式只需用到加法、乘法和迭代运算，因此大大降低了编程的难度。

基于FIR数字滤波原理，假定我们已经设计了两个滑动平均滤波器，阶数分别为n₁和n₂，那么我们将通过卷积运算对输入数据应用滤波器，如图9-21所示。图中矩形输入通过一次卷积后，再经过一次卷积，得到S形曲线。

位置指令需要n个采样周期接收脉冲串，脉冲串总数为V_maxT_s，T_s为系统采样时间。为方便叙述，令T_s=1，则矩形输入可表示为

V（k）=V_max且0≤k≤n （9-42）

经过n₁阶滑动平均滤波器

H₁（k）=n¹₁且0≤k≤n₁ （9-43）

由式（9-41）得到一次卷积：

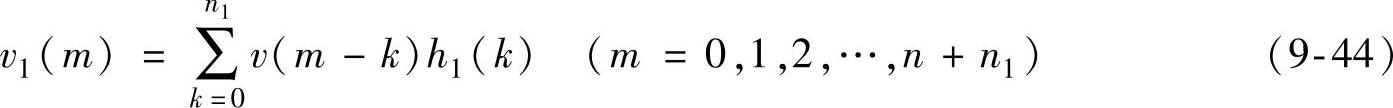
式中，m＜k时，v=0。

然后将卷积后的结果作为输入，再经过n₂阶滑动平均滤波器

由式（9-44）得到二次卷积(www.xing528.com)

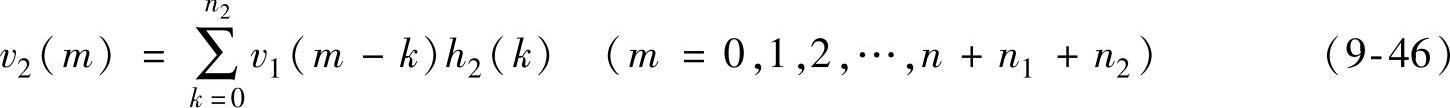
式中，m＜k时，v₁=0。

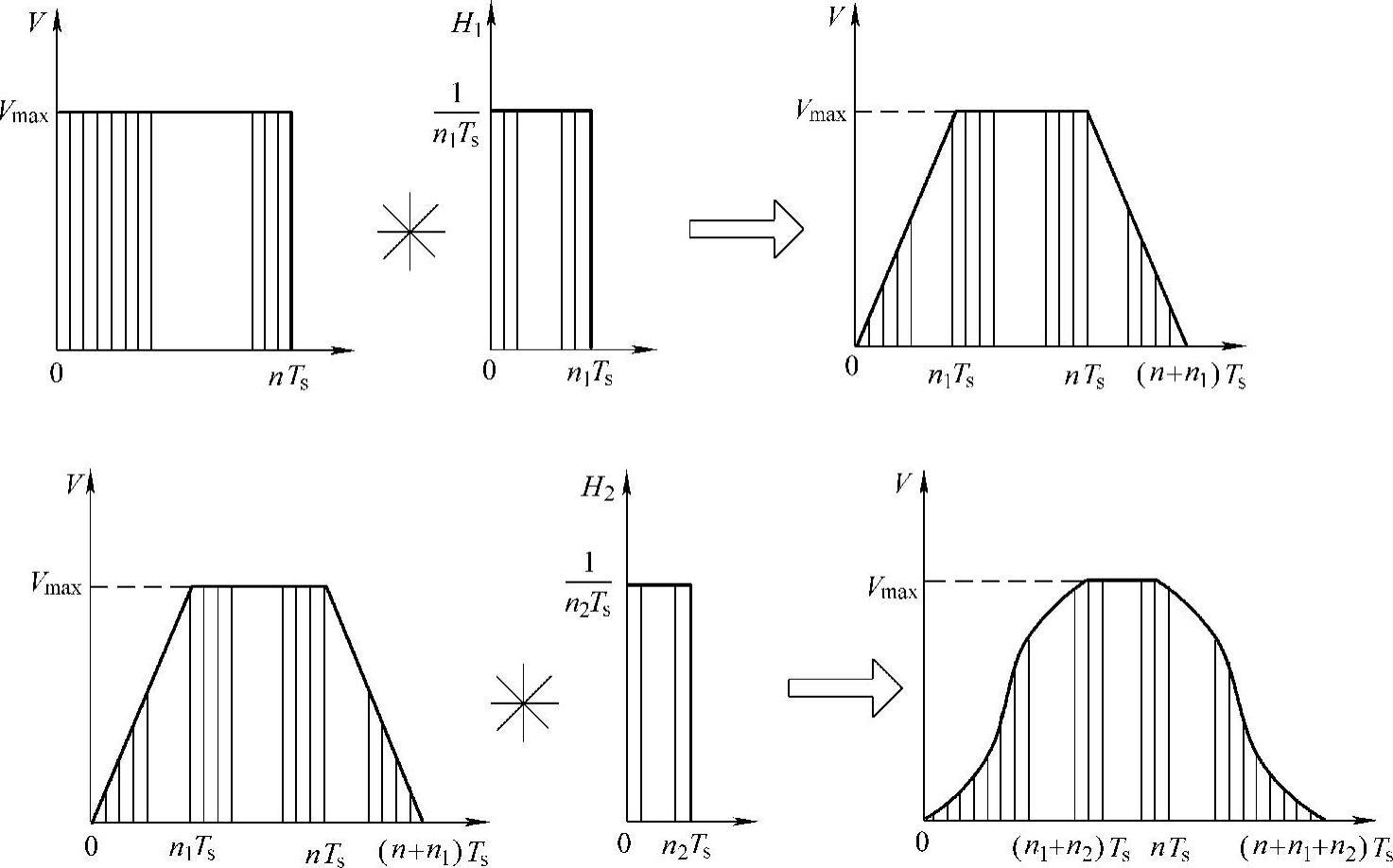
图9-21 2次卷积

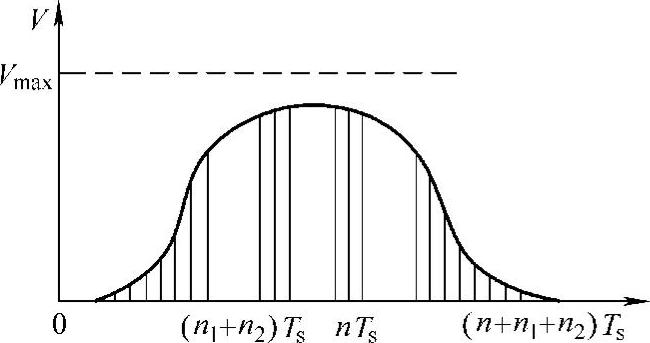
图9-22 n＞2n₁的情况

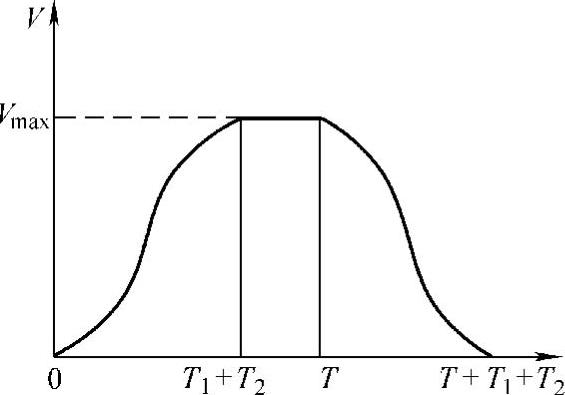
图9-23 2次卷积后的S形曲线

因此，2次卷积后的结果即是S形曲线，（n₁+n₂）称为加减速时间。该方法实际上是位置指令依次通过了两个滑动平均滤波器。这种方法需要注意到n₁和n₂的约束关系：n₁＞n₂，而且n₁也不能太大，不要超过n的一半。否则曲线不会达到最大速度V_max，而出现如图9-22的现象。

通过2次卷积方法与传统方法比较，可推导出两者之间的关系。图9-23是2次卷积后的S形曲线，图中T₁=n₁T_s，T₂=n₂T_s，T₁+T₂速度达到最大v_max。与图9-20进行对照，可发现2次卷积与式（9-40）各段时间的关系为

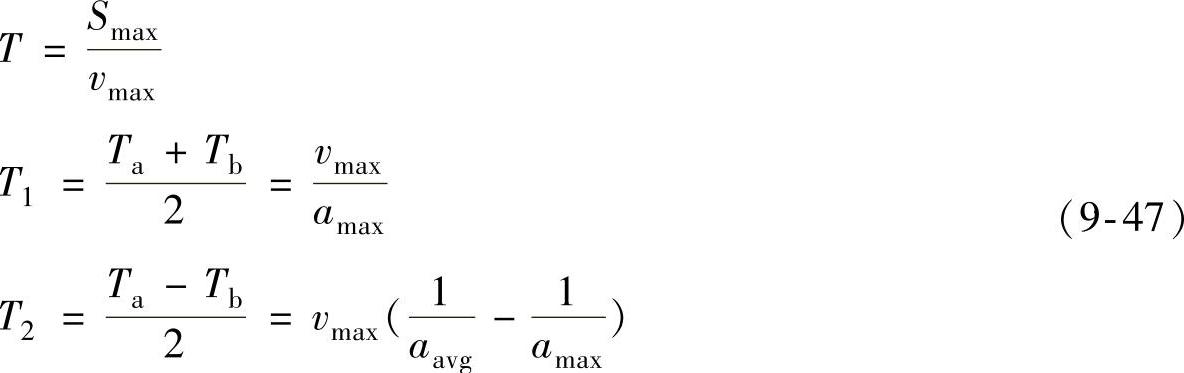
所以，基于2次卷积的S形加减速方法和传统的S形加减速方法是等效的。T₁和T₂的时间可以由S_max、v_max、amax和aavg设定，且T₁＞T₂，为确保其速度命令必会达到最大速度值，T≥2T₁。