基于IIR方式的实现方法优化

与模拟滤波器相比，数字滤波器具有很多突出的优点，例如它可以满足滤波器对幅度和相位特性的严格要求，可以避免模拟滤波器所无法克服的电压漂移、温度漂移等问题。用DSP实现数字滤波除了具有稳定性好、准确度高和不受环境影响等优点外，还具有灵活性好的特点，可通过修改滤波器的参数十分方便地改变滤波器的特性。

对许多应用来说，数字滤波器一般具有如下差分方程：

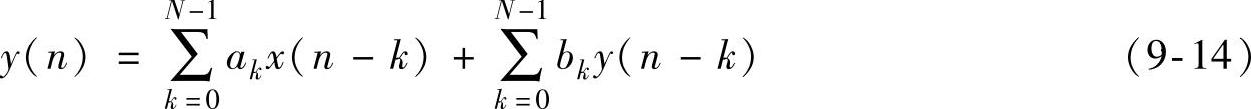
式中 x（n）——输入序列；

y（n）——输出序列；

a_k和b_k——滤波器系数；

N——滤波器的阶数。

式（9-14）具有无限长的单位脉冲响应，在结构上存在反馈回路，是递推型滤波器。也即是说，滤波器的输出不仅与输入有关，而且与过去的输出有关。当一个时刻的输入施加到这个滤波器，由于有分辨率的限制，它永远不会下降到零。因此，式（9-14）表示的数字滤波器称为无限冲击响应（Infinite Impulse Response，IIR）滤波器。

IIR滤波器由于具有结构简单、运算量小的特点，因而得到了较广泛的应用。基于IIR滤波器的实现通常有以下三种：

①以模拟滤波器函数为基础的变换法，即先设计一个满足指定条件的模拟滤波器H（s），再将H（s）转化为数字滤波器H（z）。

②直接设计法，即在z平面内，根据零、极点对系统特性的影响，调整零、极点位置，得到数字滤波器H（z）。

③最优化设计法，即在某种最小化误差准则下，建立差分方程系数a_k和b_k对理想特性逼近方程，使用迭代方法解方程组得到最佳逼近系统。由于此方法计算量大，需要借助计算机进行设计，又称计算机辅助设计法。

本节着重研究第一种方法，即由模拟滤波器设计数字滤波器的方法。为了从模拟滤波器设计IIR数字滤波器，必须先设计一个满足技术指标的模拟原型滤波器。前面分析的低通和陷波滤波器具有巴特沃斯（Butterworth）滤波器原型特征，利用这个原型，设计者只需把它由s域到z域进行变换，这个变换应遵循一定规则，具体可参考第5章“数字控制系统”5.1.5“z变换及离散化方法”所述内容。表9-1是基于阶跃响应不变思想下低通和陷波滤波器传递函数由s域到z域的变换结果。按表得到H（z）后，再取z反变换，最后得到式（9-14）的结构。

表9-1 阶跃响应不变思想下低通和陷波滤波器在s域与z域中的传递函数

设计模拟原型滤波器有多种方法，除了巴特沃斯（Butterworth）型以外，还有切比雪夫（Chebyshev）型或者椭圆（Elliptic）形等。每种原型特征在细节上各有不同，如图9-8所示。图中在相同阶数时，巴特沃斯滤波器通常最平坦，但阻带下降慢；切比雪夫Ⅰ滤波器通带等纹波（即等幅波动），但阻带下降较快；椭圆滤波器在通带等纹波，阻带下降最快，但阻带等纹波。另外，其他滤波器原型，例如切比雪夫Ⅱ阻带也下降较快，但其阻带等纹波；贝塞尔（Besell）通带等纹波，阻带下降慢，幅频特性最差，但是它具有最佳的线性相位。

设计者通常可以根据要设计的滤波器的特征，在确定模拟原型后，通过用软件在计算机上进行IIR数字滤波器的参数设计。LABVIEW和MATLAB软件都可实现这种设计，例如MATLAB软件的信号处理工具箱就提供了巴特沃斯、切比雪夫Ⅰ、切比雪夫Ⅱ和椭圆等多个函数，只要以正确的指标参数直接调用这些函数就可以很方便地对滤波器进行模拟滤波器归一化设计，并且通过双线性变换方法，正确快捷地得到设计结果。下面以设计一个切比雪夫Ⅱ型IIR低通滤波器为例来说明用MATLAB软件设计IIR滤波器的方法。(www.xing528.com)

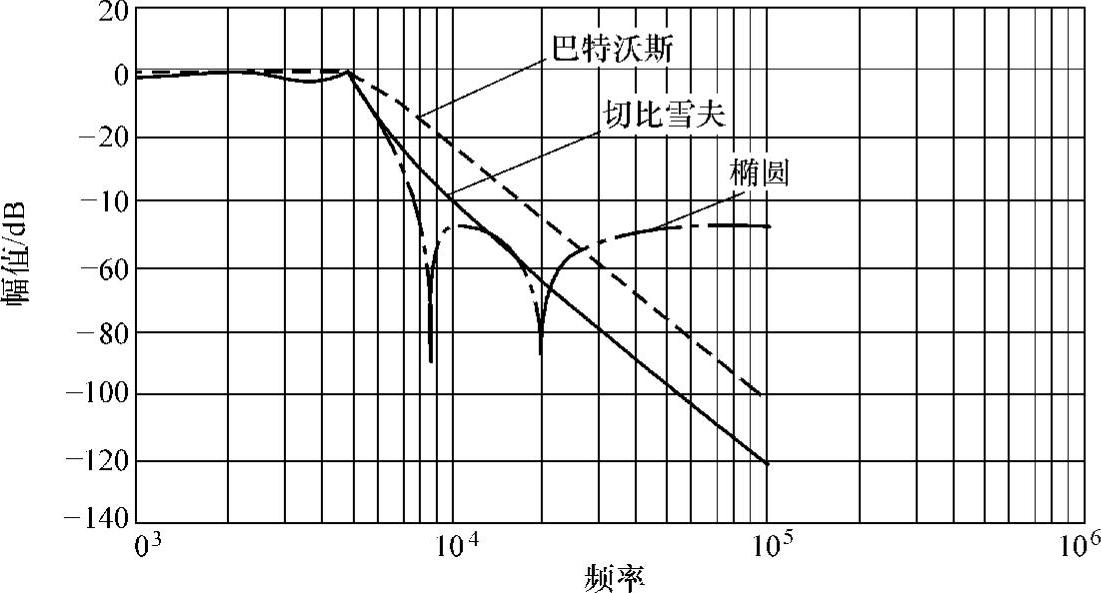
图9-8 不同模拟滤波器原型特性比较

假设要设计的滤波器特性如图9-9所示，它符合切比雪夫Ⅱ型滤波器特性，图中通带为0～λ_p，阻带为λ_s～1.0（1.0对应于半取样频率），要求通带内衰减大于R_p，阻带内波动小于R_s，则用MATLAB软件设计该滤波器的过程如下：

①调用函数cheby2ord（），确定滤波器的阶数和截止频率为

[N，ω_n]=cheby2ord（λ_p，λ_s，R_p，R_s）

返回值N为满足要求的切比雪夫Ⅱ型数字滤波器的最小阶数；ω_n为截止角频率。

②调用函数cheby2（），进行模拟低通滤波器设计，并且通过双线性变换后输出结果为

[B，A]=cheby2（N，R_s，ω_n）

返回值B为一个（N+1）维矢量，可作为式（9-14）中b多项式系数；A也是一个（N+1）维矢量，可作为式（9-14）中a多项式系数。

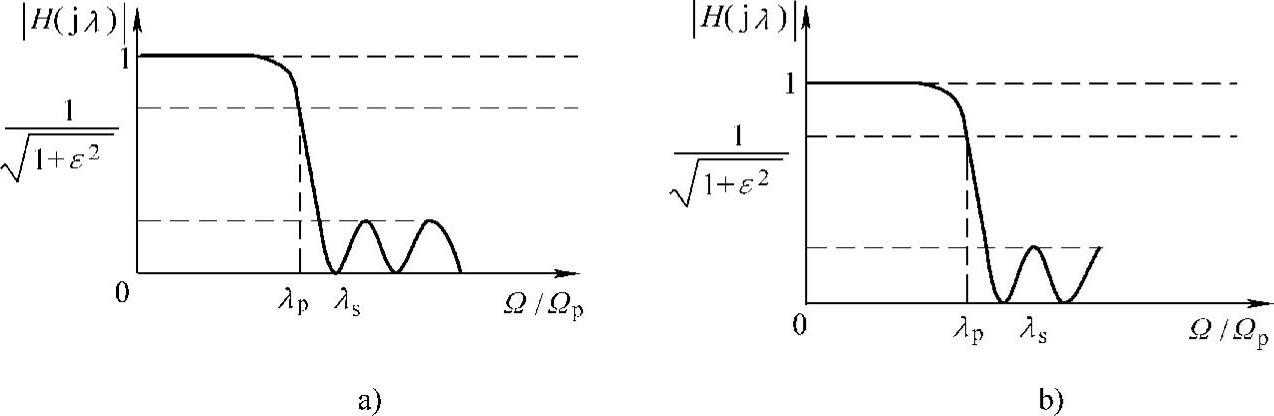
图9-9 切比雪夫Ⅱ型滤波器的振幅特性

a）N为奇数 b）N为偶数

除了低通外，陷波（带阻）滤波器设计，其切比雪夫Ⅱ函数为

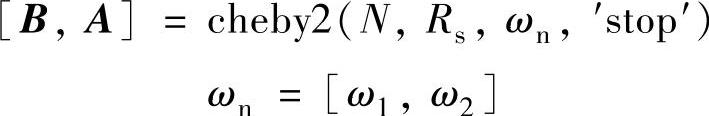
更多的函数及使用说明请参考MATLAB软件书籍中信号处理工具箱部分的相关内容。