滤波器特性与设计：二阶低通滤波器与陷波滤波器

滤波器的4种常见通带是低通、带阻、高通和带通。其中，低通滤波器和带阻（陷波）滤波器在伺服控制系统中最常用。

1.低通滤波器

低通滤波器是通过低频信号抑制或衰减高频信号的，理想低通滤波器的特性可用图9-2来说明。低通滤波器的输出电压与输入电压之比，叫做低通滤波器的增益或者电压传递函数，增益的频率特性可表示为

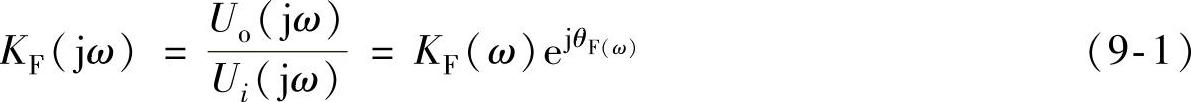
式（9-1）的对数幅频特性如图9-2所示，允许信号通过的频段为0～ω₀，这个频段叫做低通滤波器的通带，不允许信号通过的频段为ω＞ω₀，叫做低通滤波器的阻带或者禁带。ω₀叫做截止角频率，f₀叫做截止频率f₀=ω₀/（2π）。低通滤波器的理想特性是让0～ω₀频段上的全部信号通过，ω＞ω₀的信号则完全不让通过。

实际上，很难获得理想特性，实际特性将如图9-2中的曲线2或3所示，两者的差别在于通带中的幅频特性是否具有凸峰。对于没有凸峰的特性2，一般规定增益下降到K_F/2（即下降3dB）时的频率为截止频率，如a点所示。对于有凸峰的特性3，截止频率规定为幅频特性从峰值K_FM回到起始值K_F时的频率，如b点所示。

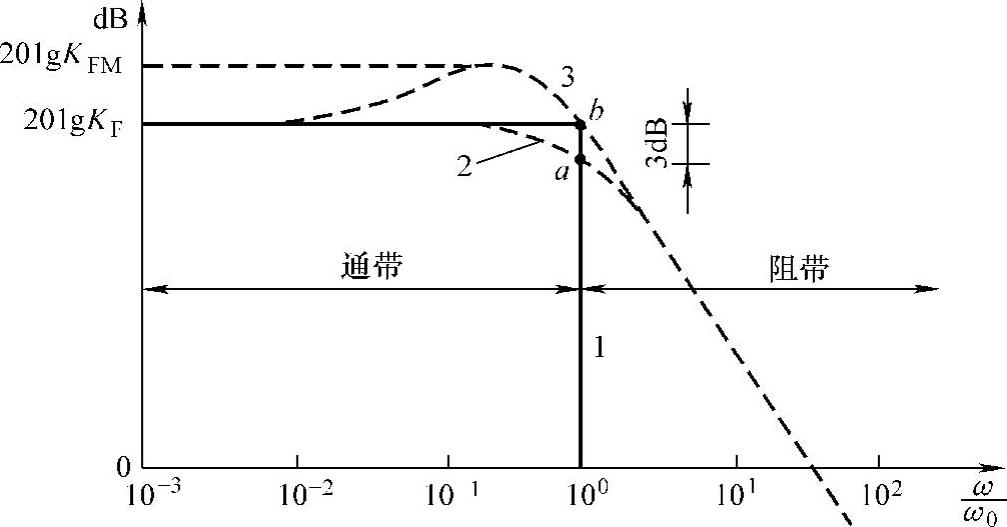
图9-2 低通滤波器的特性

1—理想特性 2、3—实际特性

基于图9-2，多数低通滤波器的传递函数没有零点，但有极点，而且极点数等于滤波器的阶次，即单极点为一阶，双极点为二阶，N极点为N阶。为方便讨论，本章以后讨论的所有滤波器的直流增益K_F（ω=0）都为1，因而图9-2中20lgK_F以后要改写为零。

（1）一阶低通滤波器

为了获得图9-2中的低通特性，方法很多，最简单的是单极点低通滤波器，其传递函数

有时，单极点滤波器会根据时间常数表达为

式中，τ为滤波器时间常数，它等于1/K。

按式（9-3）画出的幅频特性如图9-3所示，极点K等于滤波器以rad/s为单位的带宽，即等于图9-2中a点的ω₀。换句话说，在f=K/（2π）处的增益为-3dB，且转折斜率为-20db/dec（十倍频程）。

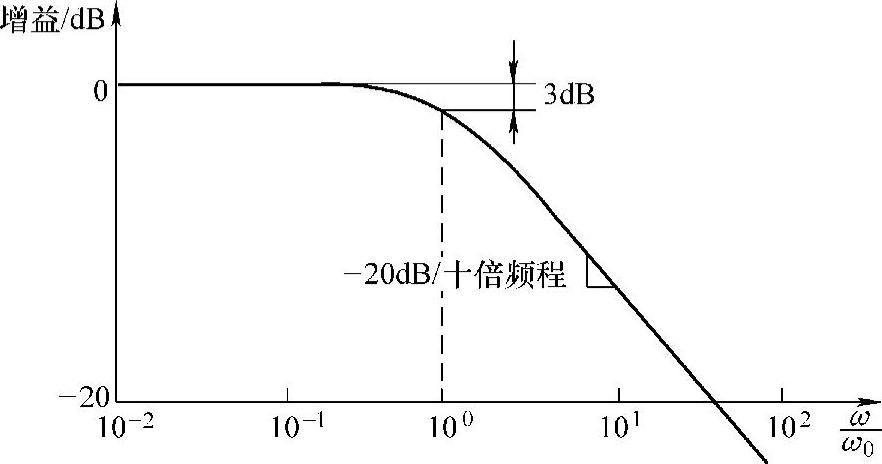
图9-3 一阶低通滤波器幅频特性

（2）二阶低通滤波器

为了增加阻带区的衰减速度，可在此使用二阶低通滤波器，它能提供-40db/dec的衰减，如图9-4所示。两极点低通滤波器的传递函数为

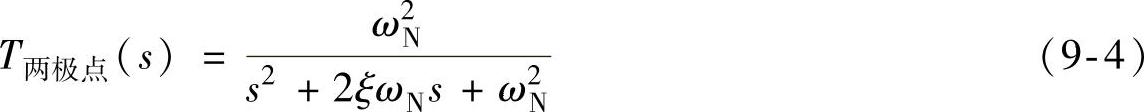(www.xing528.com)

式中 ω_N——滤波器的固有频率；

ξ——阻尼比。

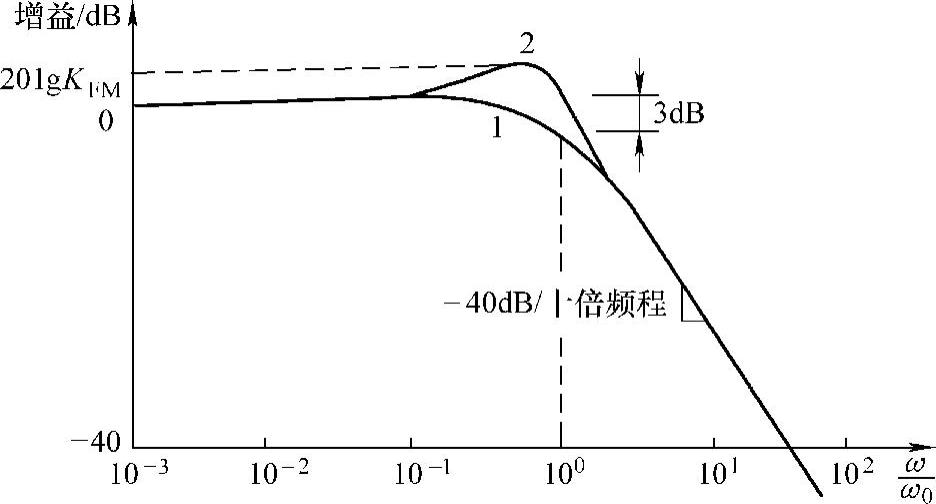
图9-4 二阶低通滤波器幅频特性

1—ξ=0.707 2—ξ＜0.707

二阶低通滤波器的各项性能主要由ξ和ω_N决定。当ξ＜1时，滤波器存在两极点，且极点是复数。如果ξ=1/2，即0.707时，没有凸峰，最大幅值等于1，此时若ω=ω_N，则幅值等于1/2，即对应3dB。可见，按-3db来定义截止频率时，ξ=1/2时的截止角频率ω_o就是固有振荡角频率ω_N，即图9-4中曲线1与图9-2中曲线2等同。如果ξ＜0.707时，滤波器将出现增益凸峰，按规定，截止角频率是幅频特性从峰值回到起始值时的角频率，为此，图9-4中曲线2与图9-2中曲线3等同。当ξ＜0.707时，ξ越小，凸峰越显著，相位滞后相对较小。

在实际应用中，两极点低通滤波器用于控制系统，它的阻尼比通常设置为0.707，因为它是在两极点低通滤波器中不产生凸峰的最小值。有时会选择ξ＜0.707的两极点滤波器，因为这样的滤波器在给定的高频处具有同样的衰减作用，而在低频段引起的相位滞后小。滤波器的这个量度对于控制系统来说是合适的，它折中考虑了高频段的衰减作用与低频段的相位滞后问题。按照这个准则，用具有较小阻尼比的滤波器在控制系统中能获得更好的性能。

2.陷波滤波器

陷波滤波器或者带阻滤波器专门抑制或衰减某一频段的信号，而让该频段以外的所有信号通过。陷波滤波器的理想特性可用图9-5来说明。陷波滤波器抑制的频段宽度叫做阻带宽度，简称带宽，用B表示。抑制带宽中点所在角频率叫做中心角频率，用ω₀表示。这样，陷波滤波器的品质因数Q由下式决定：

由式（9-5）可以得出，B越窄，则Q越高，滤波器的抑制选择性就越好。

理想特性在转折处衰减是彻底的。实际上只能获得近似的抑制特性，抑制频段的起始角频率ω₁和终止角频率ω₂按低于最大增益的0.707所对应的角频率来定义，如图中的a和b两点所示，所以带宽B和中心角频率ω₀实际中有如下的关系：

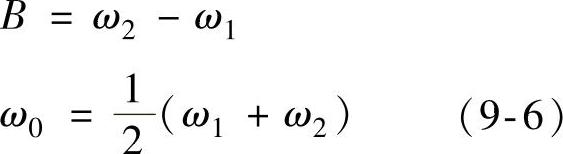
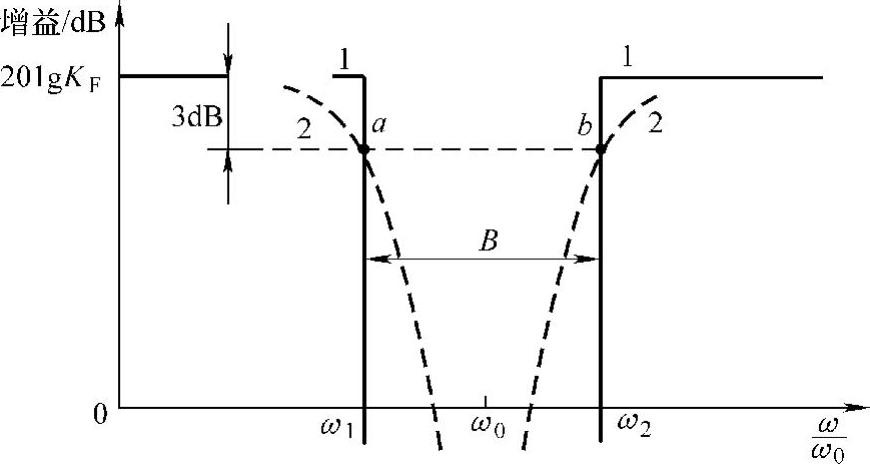
图9-5 陷波器的特性

1—理想特性 2—实际特性

传统的陷波滤波器或者带阻滤波器是二阶的，有两个极点和两个零点。其形式为

由式（9-7）可以得出，输入频率ω等于ω_N时，衰减是彻底的，增益为零。当ω远高于ω_N时，s²项在分子与分母中处于主导地位，传递函数s²/s²=1；同样，ω非常低时，s项消失，传递函数ω²_N/ω²_N=1。因此，只有ω等于或接近ω_N时，陷波器才有作用；越接近，作用越明显。在接近ω_N的这段频带内，式（9-7）会让一些输入通过（因为图9-5中2的缓慢衰减），在频带内衰减信号不彻底的原因是存在阻尼比ξ。阻尼比越小，带宽B会越窄，因而陷波品质因数Q越好，这样不但可以获得越陡峭的陷波，而且还可以减小陷波中心频率以下频率信号的相位滞后。一般而言，ξ设置为小于1，而且通常更小。

对于大多数控制系统来说，虽然实际的两极点陷波滤波器所能提供的衰减还存在限制，但是两极点陷波滤波器还是足够好地衰减了陷波频率信号。当需要在宽范围内对多个间断频率信号进行强衰减时，可将多个陷波滤波器进行级联，这样效果会更好。