基于要确定系统的类型进行PID参数整定是国内学者创造出来的一种工程设计方法。该方法是在“调节器最佳整定”(由西门子公司提出,国内习惯上称作“二阶最佳”或者“模最佳”和“三阶最佳”或者“对称最佳”)、“振荡指标法”和“模型系统法”的基础上提出的,在电动机控制的双闭环系统工程设计中获得了良好的效果,受到工程技术人员的欢迎,因而得到了普遍的应用。
应用“工程设计”法,具体地为第7章“三闭环控制系统”7.3“电流/速度环控制策略”中的电流/转速环控制器设定参数值。设计一般原则是先从电流环入手,首先设计好电流环控制器参数值,然后把整个电流环看做是转速环的一个环节,再设计转速控制器参数值。
电流控制器结构是PI控制器,其传递函数可以写成

式中 Ki——电流控制器的比例系数;
τi——电流控制器的超前时间常数。
为了让控制器零点对消掉控制对象的大时间常数极点,校正成典型Ⅰ型系统,如图8-17a所示,图中,控制器参数Ki和τi与典型Ⅰ系统的关系有

式中 Tl——电气时间常数;
R——电枢电阻;
Ks——功率逆变器增益;
β——电流反馈增益。
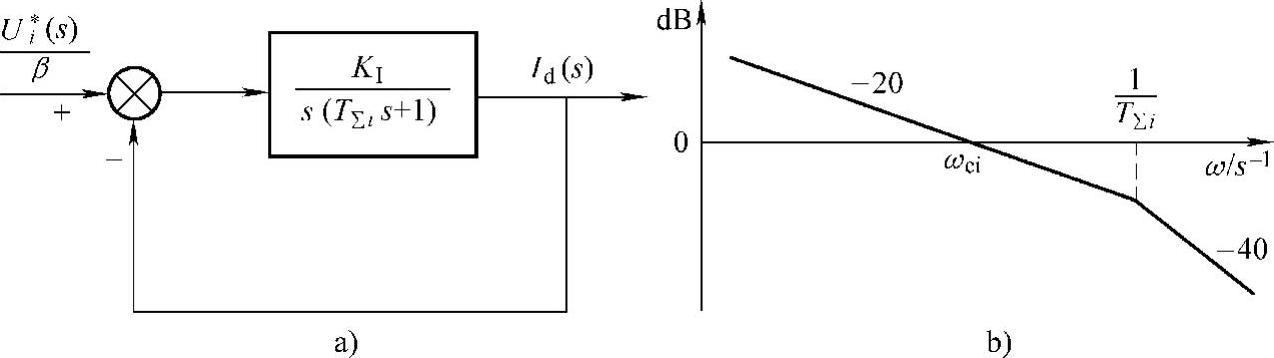
图8-17 校正成典型I型系统的电流环
如图8-17b所示,I型系统的开环传递函数中有两个参数:开环增益K和时间常数T。实际上,时间常数T往往是控制对象本身固有的,能够由控制器改变的只有开环增益K,系统开环对数幅频特性会随着K值变化而上下平移。换句话说,K是惟一的待定参数,需要找出性能指标与K值的关系。在ω=1处,典型I型系统对数幅频特性的幅值是
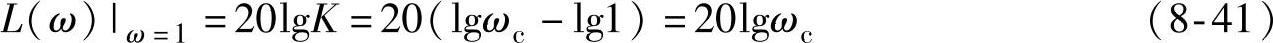
所以有

显然,有KT<1,否则图8-17b将以-40dB/dec过零,对稳定性不利。
式(8-42)也表明,开环增益K越大,则截止频率ωc也越大,系统响应就越快。前面已导出,典型I系统的相位稳定裕度是:γ=900-arctanωcT,由此可见,当ωc增大时,γ将降低,这也说明快速性和稳定性之间的矛盾。在具体选择参数时,需在两者之间折中。
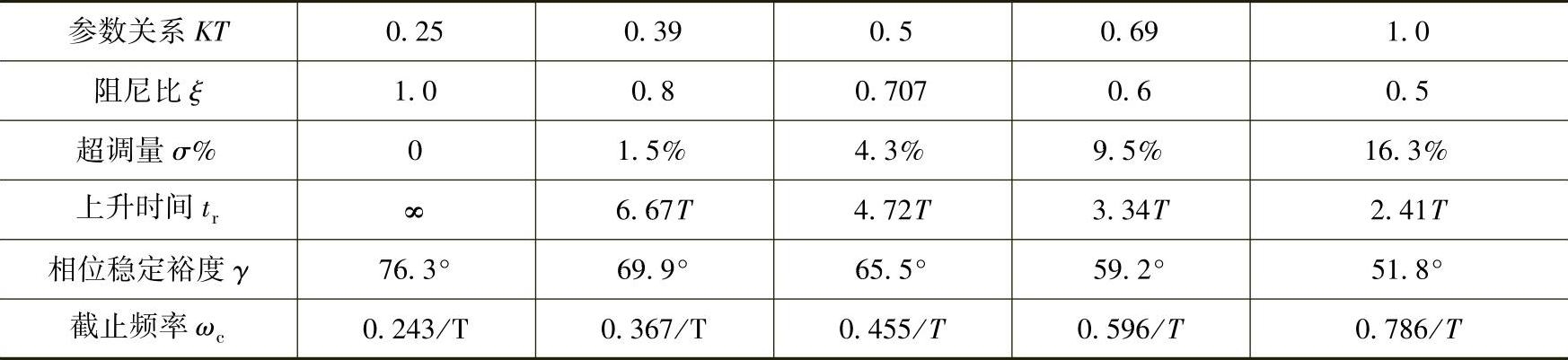
参照表8-2,确定出KT值。如果要求动态响应快,可取ξ=0.5~0.6,则KT值较大;如果要求超调小,可取ξ=0.8~1.0,则KT值较小。一般情况下,用折中值,希望超调量σ%≤5%,可取阻尼比ξ=0.707,KT=0.5,因此有

最后,电流控制器参数可以确定为
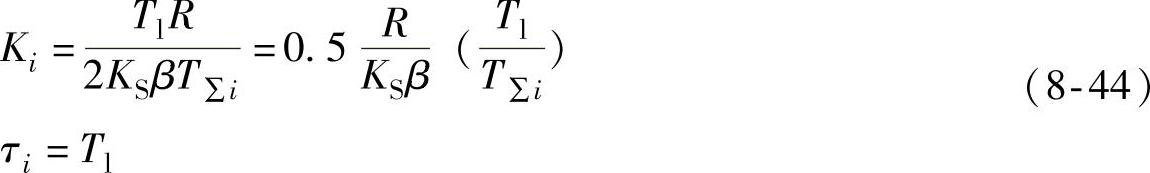
表8-2 典型Ⅰ型系统动态跟随性能指标和频域指标与参数的关系
最后,需要指出的是,如果实际系统中要求不同的跟随性能指标,对式(8-44)当然应做相应的改变。
下面确定转速环控制器的参数值。因为转速控制器结构也是PI控制器,其传递函数可写成

式中 KN——转速控制器的比例系数;
τn——转速控制器的超前时间常数。(https://www.xing528.com)
校正转速环成典型Ⅱ型系统,如图8-18a所示。控制器参数KN和τn与典型Ⅱ系统的关系有

式中 R——电枢电阻;
α——转速反馈增益;
β——电流反馈增益;
Tm——机械时间常数;
Ce——反电动势常数。
如图8-18b所示,为了方便分析动态性能,引入中频宽的变量h为

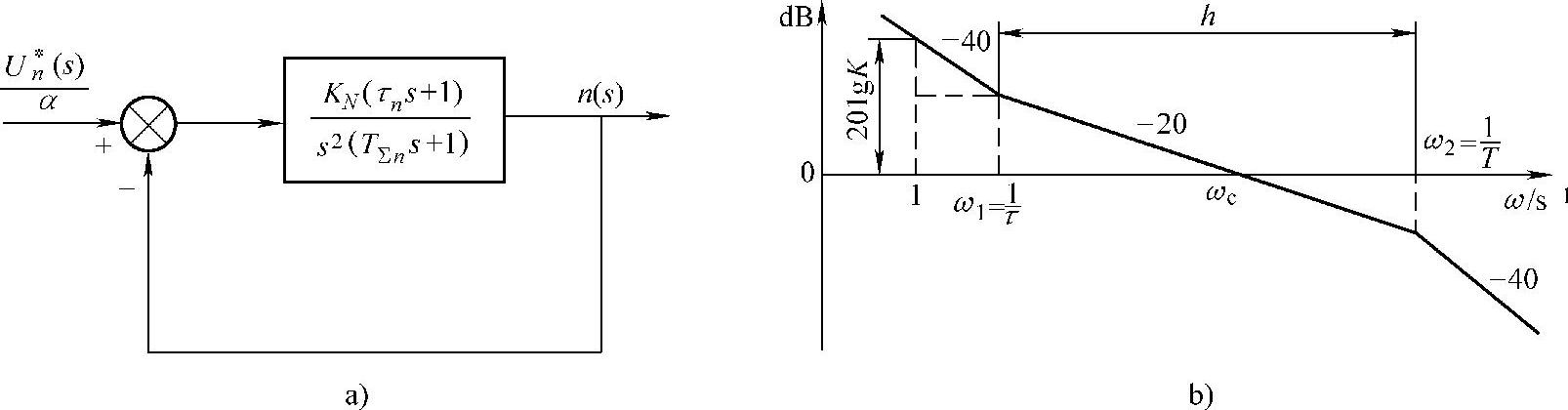
图8-18 校正成典型Ⅱ型系统的转速环
h是斜率为-20dB/dec的中频段的宽度,也称“中频宽”。由于中频段的状况对控制系统的动态品质起着决定性的作用,因此h值是一个很关键的参数。当然,它也不失一般性,设ω=1点处在-40dB/dec特性段,由图8-18b能够推导出
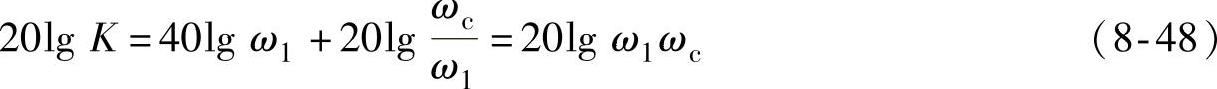
所以有
K=ω1ωc (8-49)
采用“振荡指标法”中所用的闭环幅值特性峰值Mr最小准则,来找出h和ωc两个参数之间较好的配合关系。可以证明,对于一定的h值,只有一个确定的ωc,可以得到最小的闭环幅频特性峰值Mr_min,这时ωc和ω1、ω2之间关系有

由式(8-47)、式(8-49)、式(8-50)得到
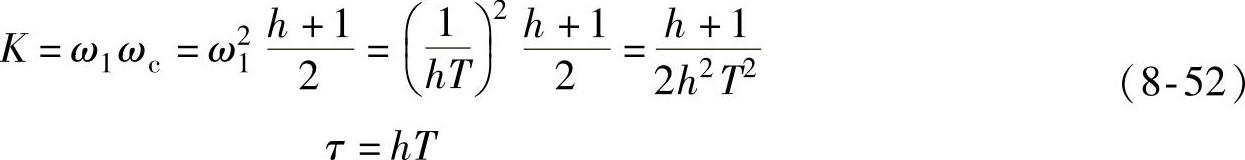
该式是工程设计方法中计算典型Ⅱ型系统参数的公式,因而式(8-46)又可以表达为

只要按动态性能指标的要求确定h值,就可以将其代入式中来计算控制器的参数。经验表明,Mr_min在1.2~1.5之间,系统的动态性能较好,有时也允许达到1.8~2.0,所以h可在3~10之间选择。h更大时,对降低Mr_min的效果就不明显了。表8-3给出了典型Ⅱ型系统阶跃输入跟随性能指标,由表能够得出,当h=5时,调节时间最短,如果要使超调低于25%,h要大于8才行。表8-4给出了典型Ⅱ型系统动态抗扰性能指标,由表能够得出,当h越小时,抗扰性能越好,但是h﹤5时,恢复时间反而拖长了。
表8-3 典型Ⅱ型系统阶跃输入跟随性能指标

表8-4 典型Ⅱ型系统动态抗扰性能指标

把典型Ⅱ型系统跟随性能和抗扰性能综合考虑,h=5是一个较好的选择。最后,转速控制器参数确定为

需要指出的是,如果实际系统中要求不同的跟随性能指标和抗扰性能指标,式(8-54)当然应做相应的改变。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




