积分饱和与抗饱和设计优化方案

在实际系统中，PID的控制量一定会因受执行机构的物理和力学性能的约束而限制在一个有限的范围里。当在这个范围内时，控制可以正常进行；一旦超出这个范围，输出就不再是计算值，而是系统执行机构的饱和临界值，从而引起不希望出现的效应。图8-9给出了带钳位（限幅）环节的PI控制器结构框图，限幅环节的输入和输出分别为u和u_s，则有

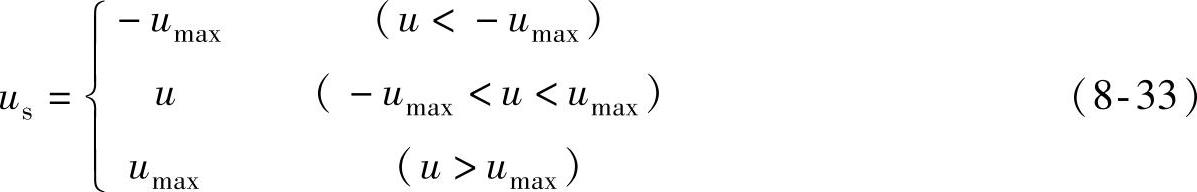
当u_s=u_max或者u_s=-u_max时，控制器饱和输出，系统处于开环运行状态。在饱和过程中，如果PI控制器的积分作用仍然有效，则误差继续累积，使得积分项持续增大，由于此时输出为非线性，使得这一过程动态时间变长，致使积分项达到很大值，而后需要持续的反符号误差来促使积分项恢复到正常状态，最终导致系统阶跃响应出现大幅振荡（又称为Windup饱和现象）。

由于主要是积分项的存在引起的饱和，因此这种饱和称为积分饱和，引起的效应称为饱和效应。积分饱和是一种非线性效应，因为系统完全被锁定，它既不说明系统的稳定性，也不表明系统响应快慢的能力，它为系统带来了非稳定性方面的超调。目前，针对饱和效应，学者进行了大量的研究，提出许多Anti-Windup抗饱和设计方法，下面给出几种典型的抗饱和设计方法。

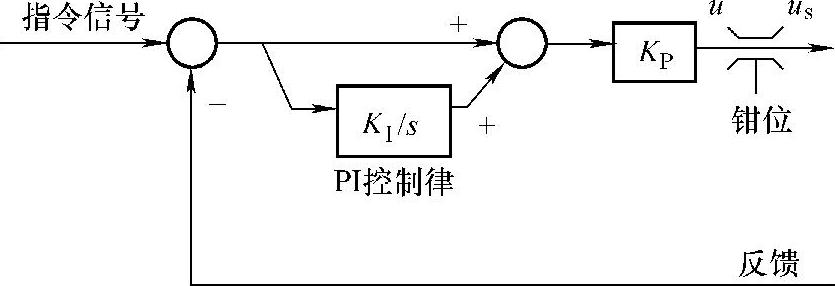
图8-9 带钳位环节的PI控制器结构框图

1.遇限消弱积分法

防止积分饱和的一种方法是遇限削弱积分法。它的基本思想是，当控制量进入饱和区后，只执行削弱积分项的累加，而不进行增大积分项的累加，如图8-10所示。图中，计算u（k）时，先判断u（k-1）是否超过限制范围u_max，如果已超过u_max，则只累计负偏差；若小于u_min（即-u_max）就只累计正偏差。最后比例、积分、微分项相加，给出控制变量。

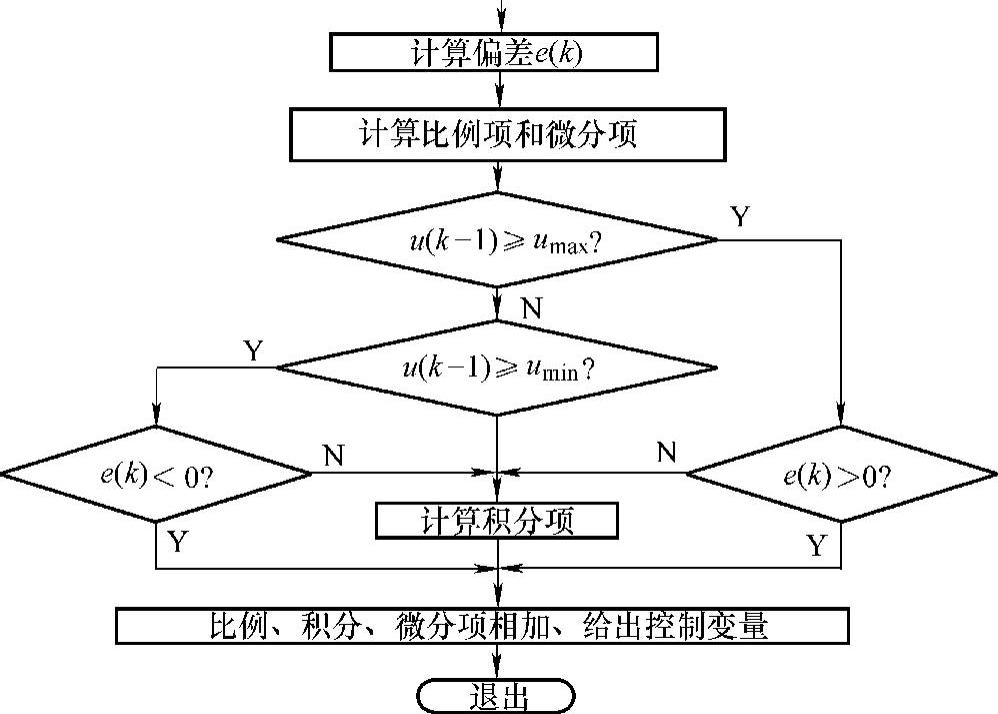
图8-10 采用遇限消弱积分法的位置式PID算法流程

遇限消弱积分法实质上是把积分钳位在某一个固定值，以防止积分器的无控制增长。虽然该方法很有效，可避免控制量长时间停留在饱和区，但是它仍允许实质上的超调。这一问题出现在：当遇限发生后，消弱的程度由积分项当前的饱和深度决定，当由于某种原因发生深饱和时，系统从饱和中退出往往还是需要较长的时间。

2.遇限保留积分法

下面介绍防止积分饱和的另一种方法，即遇限保留积分法。它的基本思想是，当控制量进入饱和区后，使得系统总是处于临界饱和，如图8-11所示。

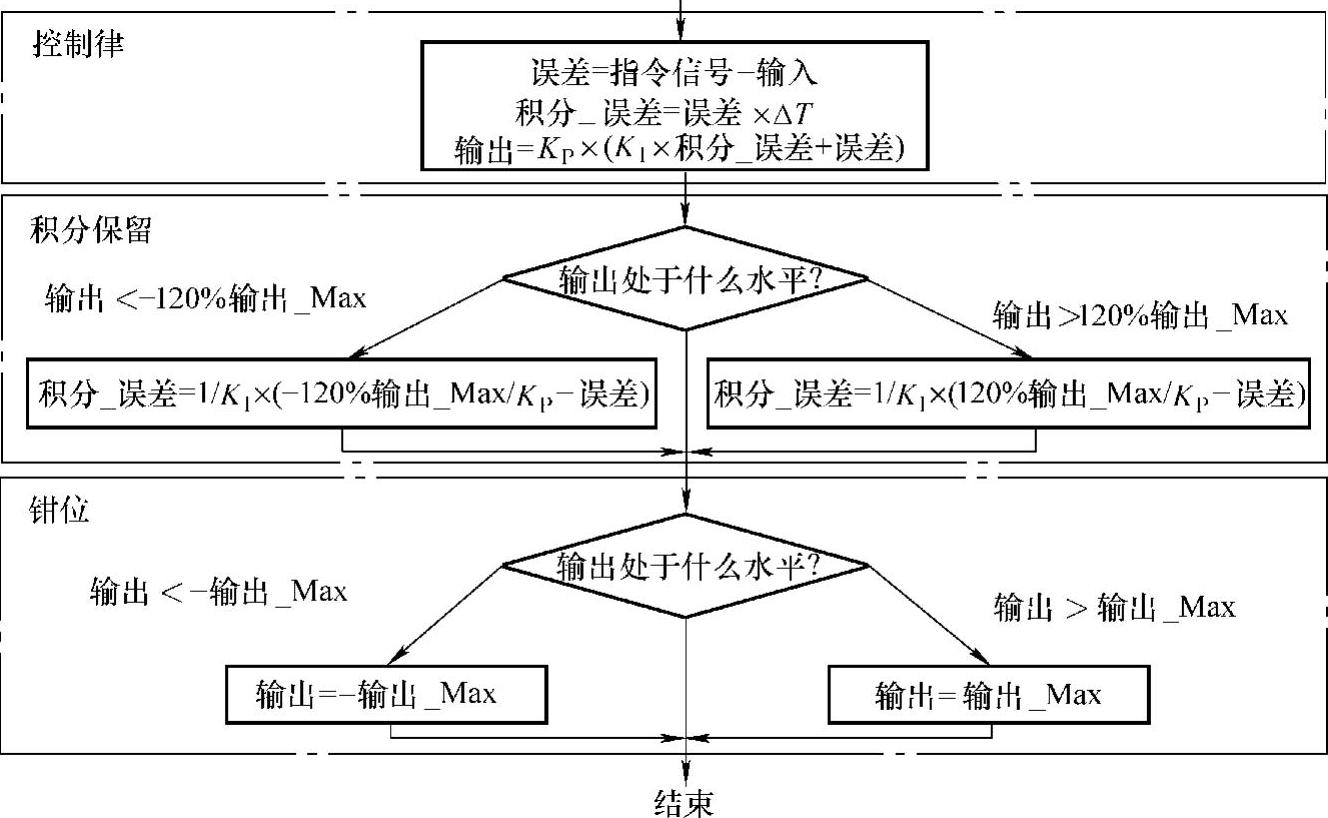
图8-11 采用遇限保留积分法的位置式PI算法流程

图中，先判断u（k）处于什么水平，如果u（k）的绝对值超出了1.2倍的u_max，则进行积分限制，并按图中函数关系保留积分。这种方法意味着积分深度是偏差的函数，其结果使得系统总是处于刚好饱和状态，即系统一旦进入饱和，会很快退出饱和。最后环节，算法对控制律的输出实现钳位，如果u（k）的绝对值超过了u_max，则输出被钳位，钳位值即为u_max；若绝对值小于u_max，就正常输出。(www.xing528.com)

3.反计算Anti-Windup法

前面两种方法由于都使用了开关（有条件积分），当PI控制器产生饱和限幅时，切换开关状态来完成消弱或保留积分作用，它们的结构是非线性的。而下面介绍的反计算Anti-Windup法（简称AW法）是将限幅环节的输入u减去输出u_s得到的误差值作为反馈信号引入至积分环节，达到抑制Windup现象的目的，它不需要使用开关，其结构是线性的。图8-12给出了反计算AW法的结构框图，由于u＞u_max，负反馈量可以对积分项进行抑制，防止控制器产生积分饱和。

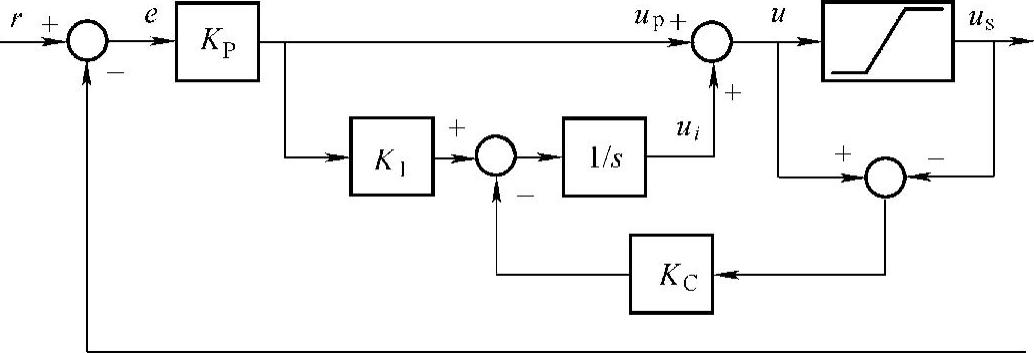
图8-12 反计算AW法的结构框图

由图8-12可推导得到线性PI控制器的输出为

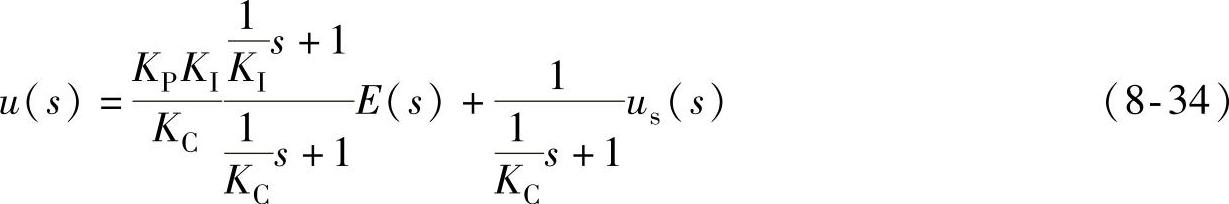
式（8-34）表明，在PI控制器参数固定不变的条件下，当控制器产生饱和时，其积分项u_i的增大或者减小取决于反馈积分增益K_C相对于积分增益K_I的大小。如果K_C非常大，即反馈补偿作用为零；随着K_C的减小，反馈补偿的抗积分饱和作用逐渐增强；当K_C减小到小于K_I时，系统出现明显的提前退饱和现象。当K_C=K_I时，则根据式（8-34）可以简化为

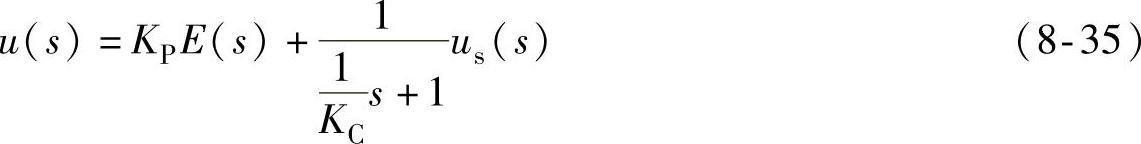
由式（8-35）得到反计算AW法的另一种结构框图如图8-13所示。

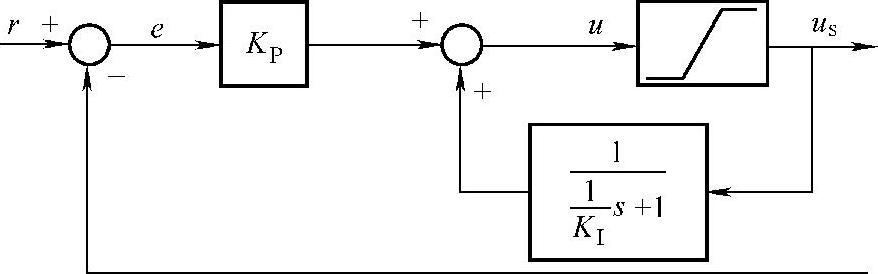
图8-13 另一种反计算AW法的结构框图

图中，在控制器处于非饱和状态下，即u=u_s，可得

此时的控制器即为线性PI控制器结构，即式（8-27）中K_D=0的情况。