数字积分和微分的应用掌握技巧

在本节讨论数字信号的积分法和微分法之前，首先介绍一下差分变换。差分变换源自数值积分的基本思想，常用来实现连续系统离散化的近似等效。根据采用差分方式的不同，可分为后向差分和前向差分两种。

（1）后向差分变换法

在后向差分变换法中，一阶导数近似为

式中 T——采样周期。

在这种方法中，由式（8-1）可得

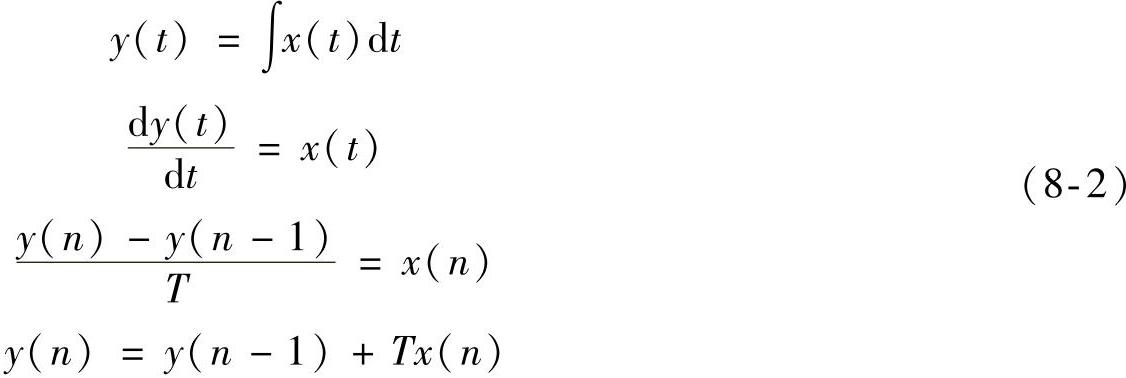
上式表明，可用矩形面积和来代替积分，在时域中的近似情况如图8-2所示。显然，当T值很小时，这种近似是可以接受的，但是当T值较大时，近似则带来较大的误差。

对式（8-2）进行整理，得到z域的积分：

于是，后向差分变换法在复频域中，s与z的关系为

根据式（8-4），s平面与z平面的映射关系如图8-3所示。图中，s平面的左半平面映射在z平面的圆心为z=1/2、半径R=1/2的圆内。

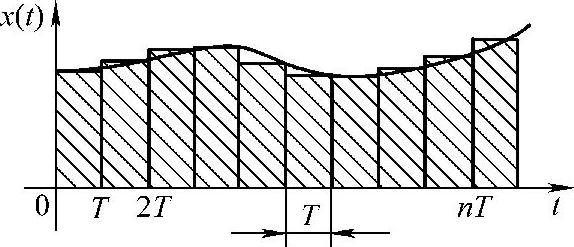
图8-2 后向差分变换法时域近似示意图

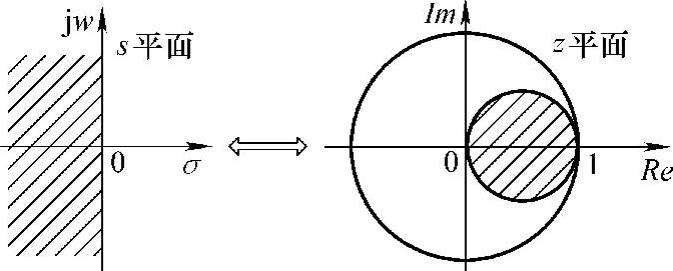
图8-3 后向差分变换法的复频域映射关系

由式（8-4）的关系，传递函数G（s），采用后向差分变换法离散化后为

根据函数在s平面和z平面的稳定域可知，如果G（s）稳定，则变换后G（z）一定也稳定；但是，反之不一定成立。最后，由式（8-5）容易验证，G（s）在s=0时，与G（z）在z=1时相等，即离散化后，稳态增益不变。

（2）前向差分变换法

在前向差分变换法中，一阶导数近似为

在这种方法中，由式（8-6）可得

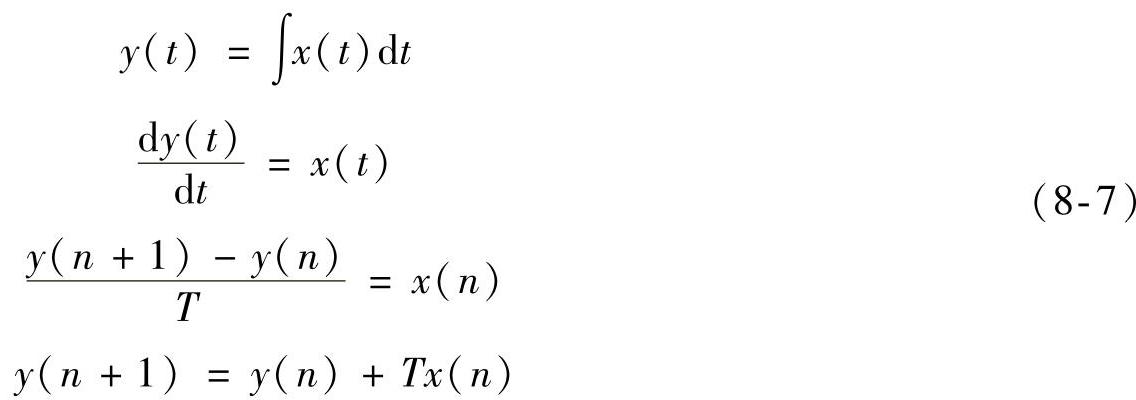
同后向差分变换法一样，式（8-7）也可用矩形面积和来代替积分，在时域中的近似情况如图8-4所示。显然，当T值很小时，近似也是可以接受的，但是当T值较大时，近似则带来较大的误差。

对式（8-7）进行整理，得到采用前向差分变换法的z域积分：

于是，前向差分变换法在复频域中，s与z的关系为

根据式（8-9），s平面与z平面的映射关系如图8-5所示。图中，z平面中的单位圆映射在s平面以（-1/T，0）为圆心、1/T为半径的圆内。

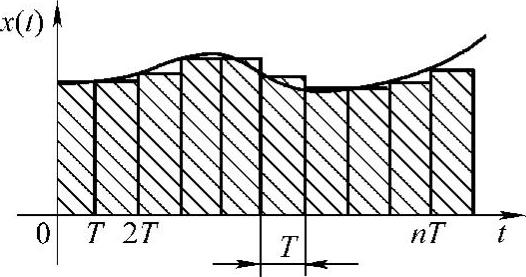
图8-4 前向差分变换法时域近似示意图

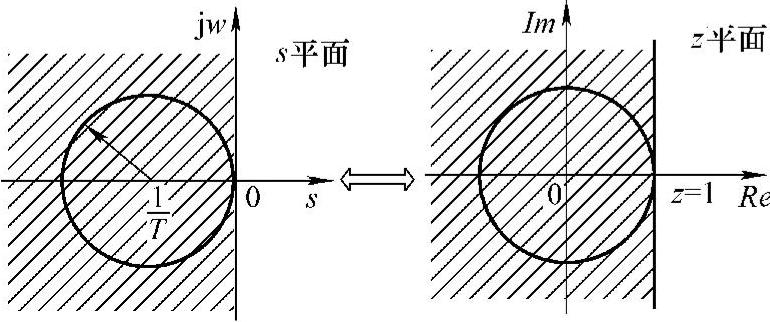
图8-5 前向差分变换法的复频域映射关系

由式（8-9）的关系，传递函数G（s），采用后向差分变换法离散化后为

于是，如果G（z）稳定，则变换后G（s）一定也稳定；但是，反之不一定成立。当采样周期T减小时，其在s平面上的映射圆面积相应的就会增大，若s平面的映射圆中包括G（s）的全部极点，则变换后G（z）也是稳定的。最后，由式（8-10）容易验证，前向差分变换法离散化前后的稳态增益也可保持不变。

由上述分析中可得到，差分变换不能保证变换前后有对应的稳定性关系，但是它简单，且当T很小时，性能也较好。因此，在对已有模拟系统的离散化实现中，数字PID控制器经常采用后向差分变换法实现。

由此也可以看出，数字系统是不能够准确地积分或者求导的，为此采用的方法即是一个近似的过程。下面讨论几种典型的数字信号积分法和微分法。

（1）欧拉积分法

式（8-3）的方法是最常用的数字积分法，又称为欧拉（Euler）积分法，或者称为欧拉累加。图8-6给出了欧拉积分法的框图，在每个时间步长内，输入X_N乘以采样间隔T，然后由积分器输出累加值Y_N。

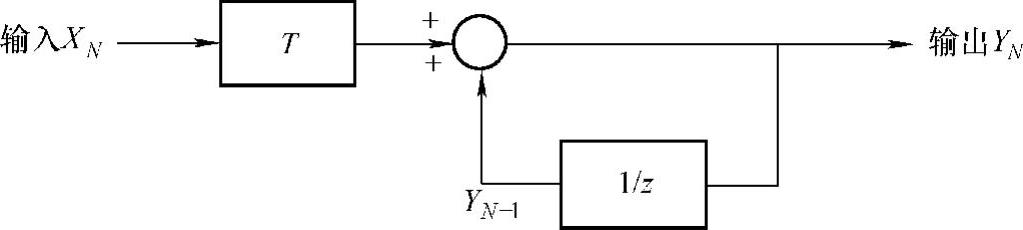
图8-6 欧拉积分法

由式（8-3）得到欧拉积分法的相位与增益为

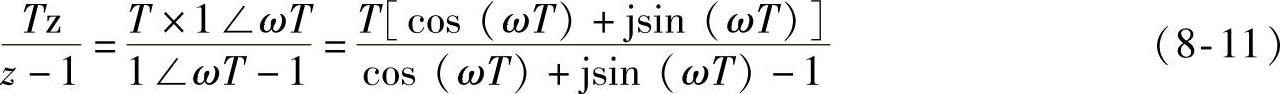
理想的积分1/s总是有一个-90°的相位和1/（2πf）的增益。而由式（8-11）可得出，欧拉积分的增益在低频时与理想积分是相似的，但是它的相位却并不那么准确。这似乎是欧拉积分法的一个缺点，但是，再次留意会发现，它的相位总是超前于理想的-90°。相位超前一般能提高稳定性，从这种意义上来说，由于一般情况下，相位滞后是有害的，所以对于控制应用来说，欧拉积分法优于理想积分。

对于控制系统来说，欧拉积分法是最常见的积分法，诸如PID这样的控制方法并不需要准确的积分也能运行得很好，因为积分通常把平均误差遏制为零，在长时间范围内，确保了被控信号和指令信号之间的匹配。但是在有些情况下，可能需要更准确的积分法，下面将给出欧拉积分法的备选方法。

（2）积分备选方法(www.xing528.com)

我们知道，后向差分变换法来自数值积分的思想，一个定积分可表示为

它的几何意义是曲线图形的面积。从定义可知，定积分的基本分析方法有4步，即分割、近似、求和以及取极限。

①分割就是把总量（整个曲形面积）分成若干分量；

②近似就是在每个分量中用容易计算的量去代表；

③求和就是把分量加起来得到总近似值；

④最后取极限就是得到积分准确值。

式（8-2）就是采用矩形去代表分量的，它存在一定的近似准确度，如果需要更为准确的积分，应该构建更加准确的插值求积公式。

经常使用的公式是牛顿—柯特斯公式，它把[a，b]分为n等份，步长即采样周期T=（b-a）/n，则取等分点t_k构造出的插值型求积公式为

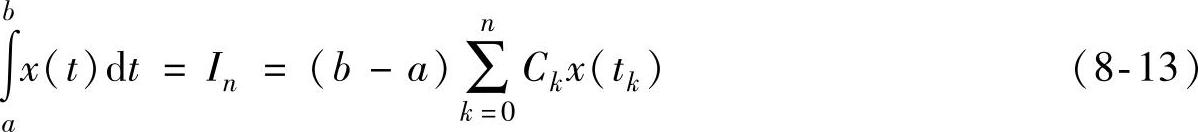
式中t_k=a+kT，（k=0，1，2，…，n）。

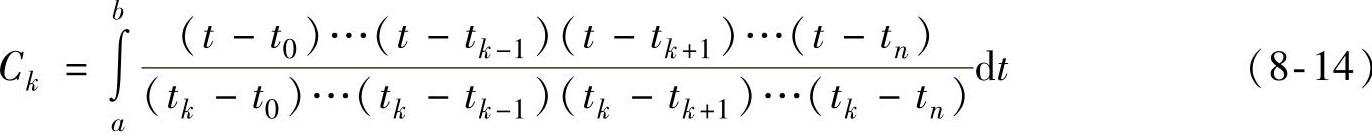
式（8-13）中，I_n称作n阶牛顿-柯特斯公式，从公式阶数的复杂度和积分近似准确度之间权衡考虑，使用一阶和二阶就可以满足要求，一阶和二阶牛顿—柯特斯公式分别又称为梯形公式和辛普森公式。当选择n=1时，由式（8-14）可计算出C₀=C₁=1/2；n=2时，由式（8-14）可计算出C₀=C₂=1/6，C₁=2/3。

梯形公式可写为

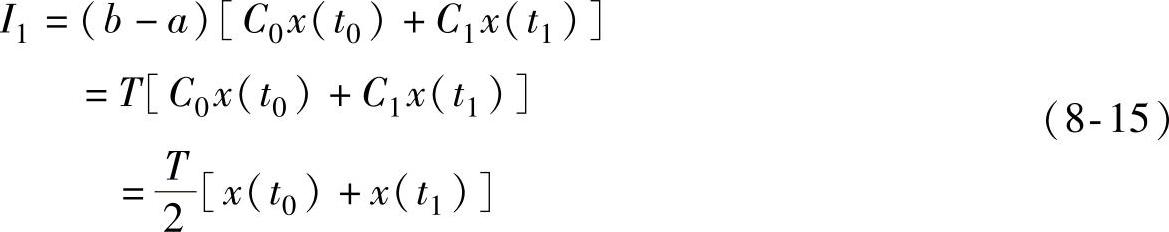
于是，可得到

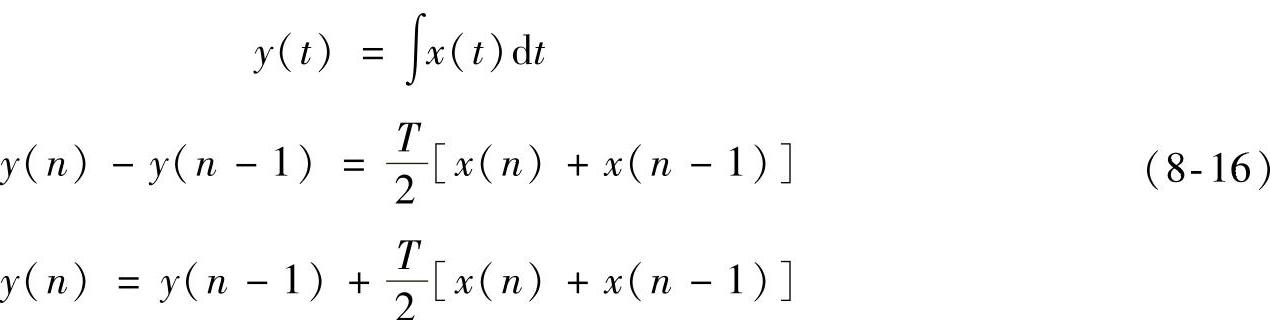
对式（8-16）整理，得到梯形法积分为

同理，辛普森公式可写为

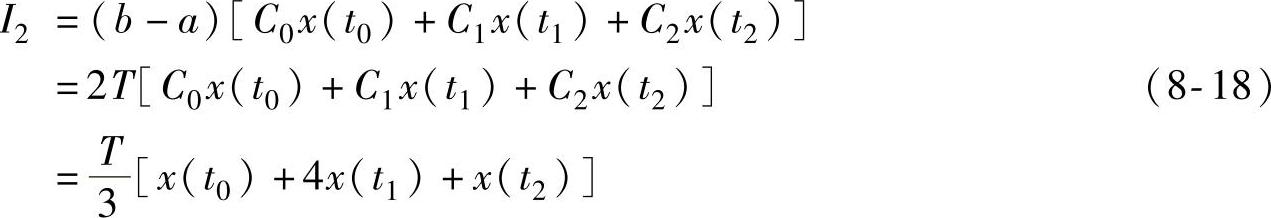
于是，可得到

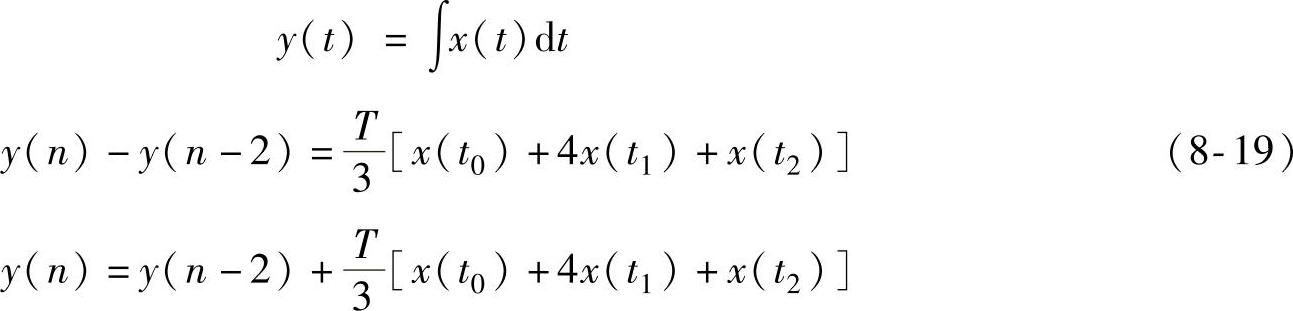
对式（8-19）整理，得到辛普森法积分为

比较式（8-16）和式（8-19），梯形公式采用当前输入值与前一输入值的平均值来近似曲线下的面积，曲线两点间用直线连接；而辛普森公式采用三点近似面积，曲线三点间用抛物线连接，因而辛普森公式比梯形公式更为准确。但是，辛普森法有个明显的缺点，它需要三个采样点，这进一步增大了辛普森法的相位滞后。因此，人们更感兴趣的是梯形公式，因为它相对简单、相对基本。图8-7给出了梯形积分的时域近似示意图和s域结构框图，与欧拉积分相比，它的近似准确度得到了提高，但代价是有近90°的相位滞后。

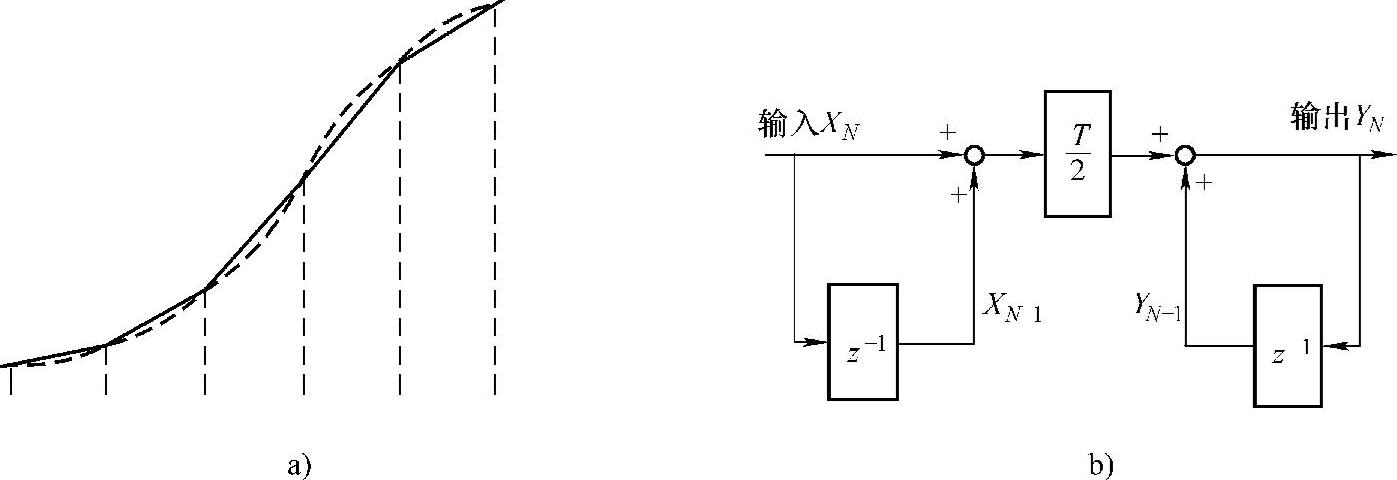
图8-7 数字梯形积分法

a）时域近似示意图 b）结构框图

（3）简单差分法

同积分一样，数字微分只是一个近似，最常见的就是简单差分法。它是欧拉积分的逆运算：

把它转换到时间域，有

从式中不难发现，简单差分（微分）法以速度估计的形式增大了相位滞后，从而降低了系统的稳定性。

（4）逆梯形微分法

虽然梯形积分法更为准确，但是它在控制系统中很少使用，因为它有90°的相位滞后，一般来说，这是不希望出现的。但是，如果采用逆梯形微分法，即用颠倒梯形积分来近似求导，将会产生理想求导所具有的90°的相位超前，实际上这是一个优点：

再把该函数变换到时间域，其结果为

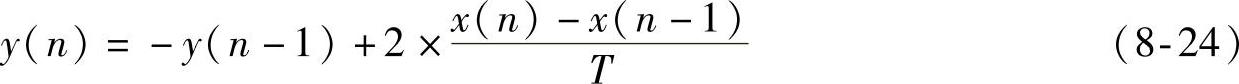
很遗憾，这个式子是不稳定的，因为如果输入x（n）和x（n-1）为零，那么y（n）就会在每一个连续采样点改变符号。学者研究表明，这个问题可以通过一种改进的方法来消除，如图8-8所示。图中，增加参数a，使得它介于简单差分（a=0）和不现实的逆梯形微分（a=1）之间。于是，把a设置为接近但小于1的值，就可以利用逆梯形微分法的主要优点，并保持算法的稳定性。改进算法如下：

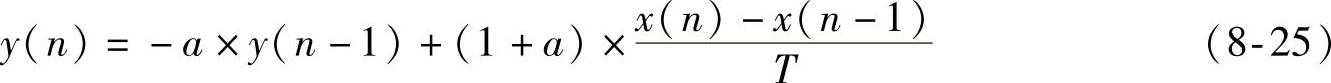
上式在z域的传递函数为

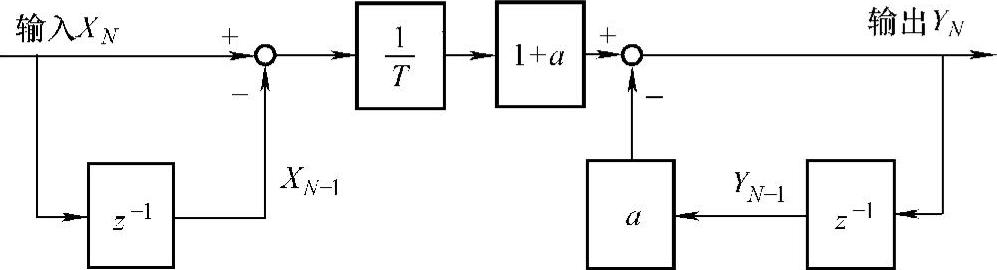
图8-8 改进的逆梯形微分法

采用改进的逆梯形微分法[即式（8-25）]，虽然a增大引起求导后的相位超前也增大，从而导致传递函数对噪声也更灵敏，但是，这种噪声的敏感性可以用更高分辨率的反馈或者系统中其他消噪源来抵消。