电动机振动模型与动力传递系统的设计优化

为了传递转矩和转速，在电动机和负载之间，存在着各式各样的机械传动机构。例如，在实际工业应用中，数控加工设备的机械结构如图7-31所示。图中，电动机通过伺服驱动器进行闭环控制，执行机构通过联轴器、传动轴以及滚轴丝杠等传动机构与电动机连接。

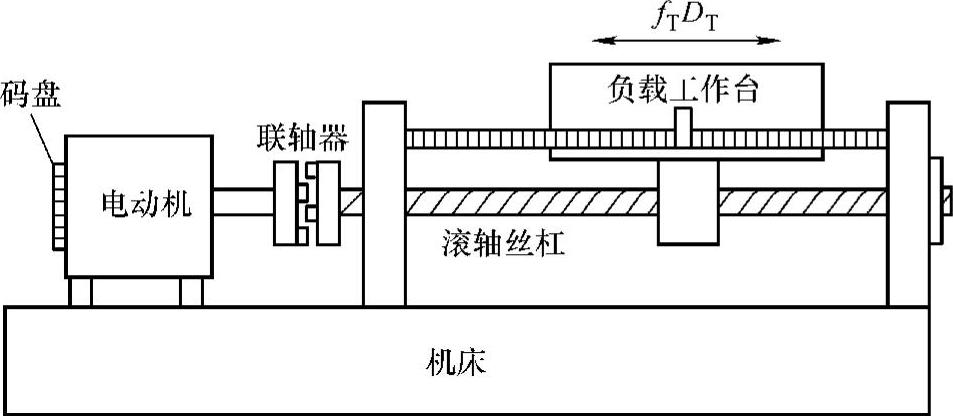
图7-31 数控加工设备机械结构

由于传动装置的刚度有限，机构中每个部件都有一定的柔性，换句话说，每个部件都可以看做是一个弹簧。由弹簧特性建立的电动机与负载模型就像图7-2b所示那样，它是一个二惯性系统的物理模型，弹性的存在将在系统中引入谐振点，引发机械谐振。一般情况下，振动负载模型的结构框图如图7-32所示。指令电流I_C通过电流控制器产生反馈电流I_F，然后与电动机转矩常数K_T相乘产生电磁转矩T_E。电磁转矩直接驱动电动机转动惯量J_M，产生电动机加速度A_M，加速度通过积分得到电动机速度V_M，进而得到电动机位置P_M。

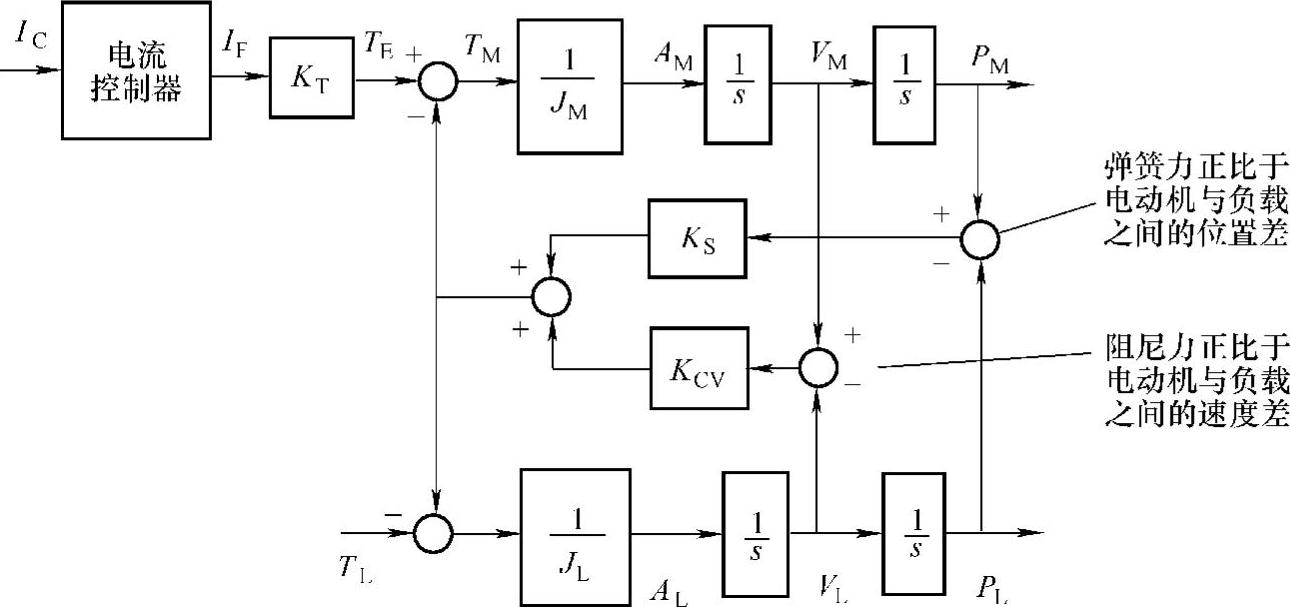
图7-32 振动负载模型的结构框图

图中，一旦电动机轴开始转动，组合的传动机构柔性变形，即弹簧弹性收紧，对负载产生的转矩正比于电动机与负载位置之差，其值为弹簧转矩K_S（P_M-P_L）。一方面，它将正向作用于负载，负载转矩T_L对负载转动惯量J_L驱动，产生负载加速度a_L通过积分形成负载速度v_L，再次积分后形成负载位置P_L；另一方面，弹簧转矩反向作用于电动机，来减缓电动机的运转。

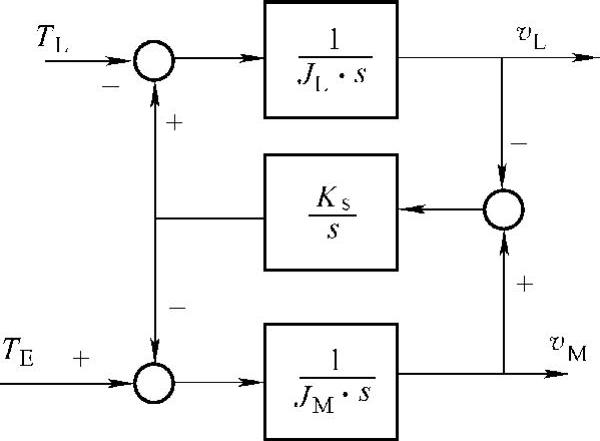
另外，图中还含有一个交叉耦合的黏性阻尼项K_cv，该项产生的转矩正比于电动机与负载之间的速度差。阻尼有利于稳定系统，很遗憾的是，常用的传动材料主要是钢，它几乎不提供机械阻尼。因而，系统中的阻尼系数很小，甚至可忽略，从而可以对系统模型进行简化，如图7-33所示。图中还忽略了静摩擦和干摩擦（Cou_- lomb摩擦）带来的影响。

(www.xing528.com)

图7-33 简化的振动负载模型框图

由图7-33所示的框图得到电磁转矩T_E到电动机转速v_M的传递函数：

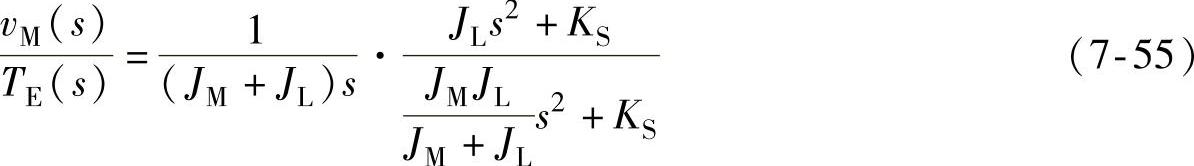
式中给出了两个结果，等号右边第一项等效于非柔性电动机特性，即积分乘以电动机和负载转动惯量之和；第二项代表了柔性耦合的作用。该式即是系统振动的数学模型。

由图7-33也可以得到电磁转矩T_E到负载速度v_L的传递函数：

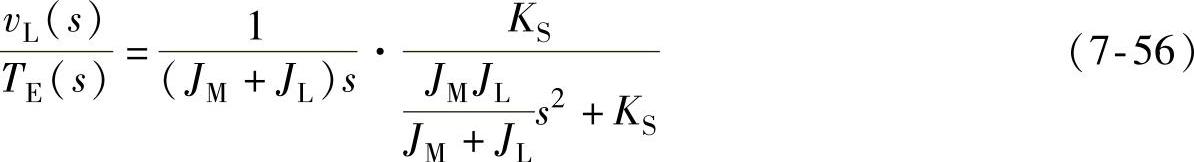
该式用来计算完全取决于负载反馈的伺服驱动系统的响应。它与式（7-55）是类似的，只是分子没有s²项。由于缺少s²项，式（7-56）在高频段多了180°的相位滞后，因此一个完全取决于负载反馈的系统通常很难控制。大多数高性能系统取决于电动机的反馈，即式（7-55），至少在高频段是这样的。当需要用负载来获得更高的准确度时，许多系统采用称为双回路控制的控制技术，这种技术采用两个反馈装置，一个安装在电动机上，另一个安装在负载上，如图7-29所示的那样。