扰动解耦法：消除控制回路中的扰动

由图7-17接着分析转速环的扰动响应。图中，扰动转矩可由扰动电流I_dL乘以转矩常数K_T得到，实际系统中，扰动转矩T_dL是转速环的扰动指令，它是负载转矩、动摩擦转矩及重力转矩等转矩之和，其转矩扰动传递函数可由式（7-36）得到为

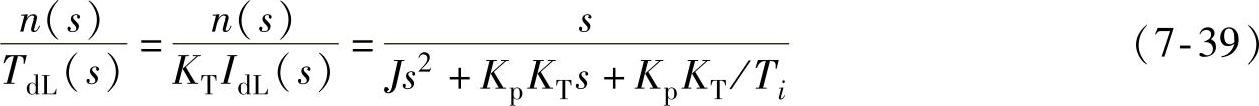
由上式得到的抗扰动幅频特性如图7-19所示。

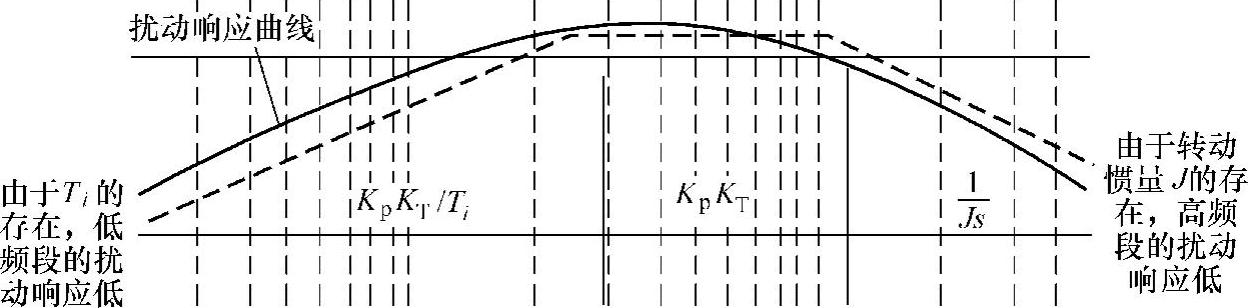
图7-19 转速环扰动响应的频域图

高频时，s比较大，Js²在分母中处于支配地位，于是：

它近似为一个有增益的积分环节，转动惯量的增大改善了高频段的扰动响应，并且它与转速调节器参数无关。

扰动响应在中频段时，式（7-39）分母中K_pK_Ts占主导地位，于是有

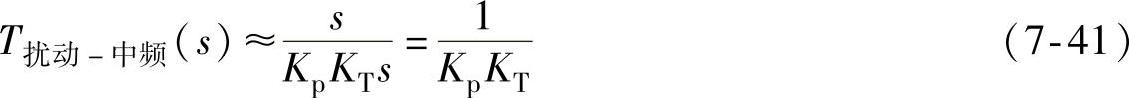
它近似为一个恒增益环节，正如式（7-41）所表示的那样，更大的比例增益有助于改善中频段的扰动响应性能。

在最低的频率范围内，s非常小，因此K_pK_T/T_i占据主导地位，式（7-39）可简化为

比例增益的增大改善了低频段的扰动响应，同样减小积分时间也是一样的。

根据上述分析，转速环的扰动响应可以在整个频率范围内由式（7-40）～式（7-42）近似，在高频段由J支配，与转速调节器PI参数值无关；比例参数改善了中、低两个频段的扰动响应，而积分参数只改善低频段响应。(www.xing528.com)

由此可见，改善扰动响应最直接的方法是提高控制器的增益。但是，所有的系统都存在稳定性限制，这种限制限定了回路的高增益。因此，另一种改善扰动响应的方法为扰动解耦法。扰动解耦法首先对扰动进行测量或估计，经过解耦路径引入到控制回路中，近似消除扰动。它的优点是当小稳定裕度不允许回路增益增大时能改善扰动响应，其缺点是必须对扰动进行测量或者估计。扰动解耦法与增大回路增益的方法并没有排他性，即两者一起使用可以获取的扰动响应优于单独用其中任何一种方法所获得的扰动响应。

图7-20给出了转速环扰动解耦的一般形式。按图中所示，扰动响应传递函数为

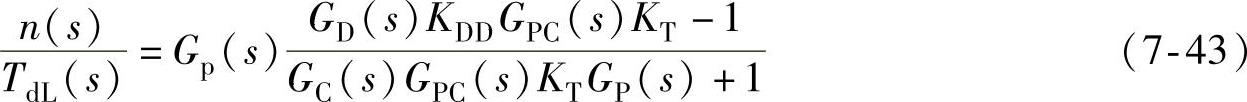
观察可以发现，假定K_DD=1/K_T，如果解耦路径G_D（s）是电流环G_pc（s）的逆，那么对扰动的响应将是理想的，即分子为零。理想的扰动解耦的结果与转速环控制器的增益无关，当电流环简化为1时，扰动量测量准确度就成为实现对扰动理想响应的关键。理想的测量是不现实的，而实际中电流环G_pc（s）也并非为1，构建电流环的逆是相当复杂的，花费巨大的代价可能只会换来较低的测量扰动带宽G_D（s），和较低的测量扰动准确度K_DD。因此，扰动解耦法的研究重点在于如何理解扰动测量缺点的含义，具体地说是在于如何理解电流环的逆的缺点含义。

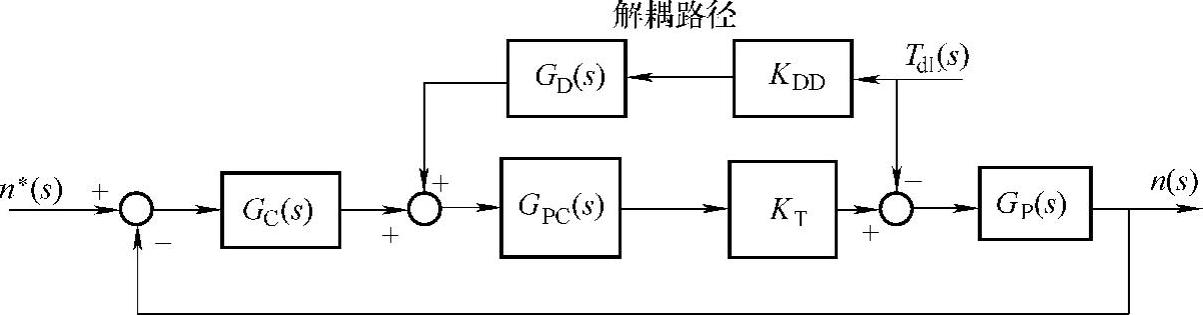
图7-20 扰动解耦法一般形式

G_C（s）—ASR传递函数 G_PC（s）—电流环传递函数 G_P（s）—1/JsG_D（s）—测量扰动带宽 K_DD—测量扰动准确度

作为直接测量的一种备选方法，扰动转矩可以通过估计或者观测获得。通常把扰动转矩作为阶跃函数来处理，并以此构成0阶扰动观测器，如图7-21所示。图中是利用速度信号的0阶扰动观测器，其观测出的扰动转矩为

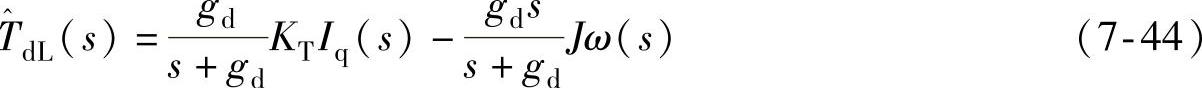
式中 g_d——扰动观测器的极点，是决定状态观测速度的一个参数。

根据式（7-44）的0阶扰动观测器所构成的关于转矩（电流）的Ⅰ型伺服系统，在稳定状态时，它可以完全抑制阶跃状态输入的扰动转矩，观测扰动转矩与扰动转矩可以表示成

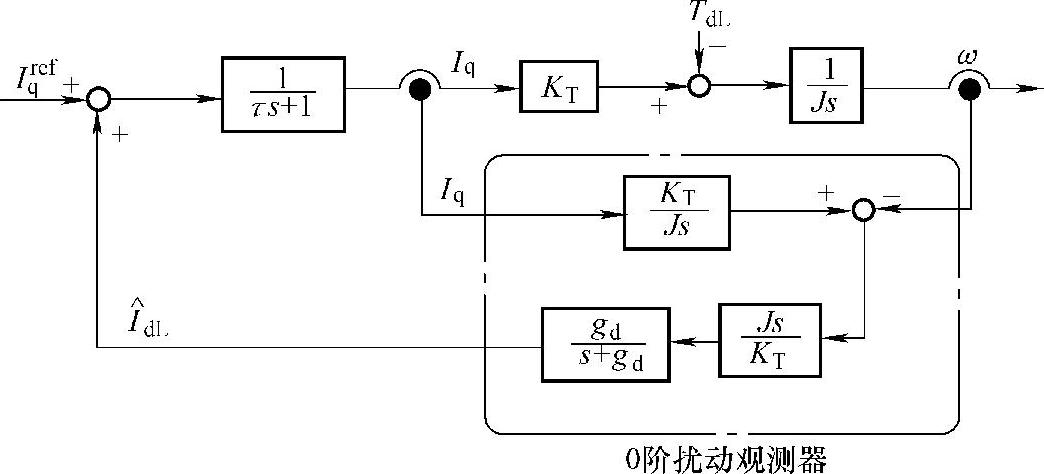
图7-21 基于0阶扰动观测器的扰动估计