误差与稳态误差的探究与分析

如果对图7-3a进行改造，把传递函数G（s）分成两部分，并且在中间加入了扰动量输入，如图7-9所示。该图比较接近实际系统，当输入信号R（s）与主反馈信号B（s）不等时，比较装置的输出为

此时，系统在E（s）信号的作用下产生动作，使输出量趋于希望值。通常，称E（s）为误差信号，简称误差（也称偏差）。

在扰动信号N（s）作用下，其扰动误差为

比较式（7-20）和式（7-21）可知，由于信号作用在系统中的位置不同，产生误差的结果会不同。如果把扰动信号看作是一种特殊的输入信号，那么，系统的误差可以描述为是多个输入信号作用在系统上产生的误差的叠加。

误差本身是时间的函数，其时域表达式为

e（t）=e_ts（t）+e_ss（t） （7-22）

上式把误差信号e（t）分成两部分：瞬态分量e_ts（t）和稳态分量e_ss（t）。由于系统必须稳定，故当时间趋于无穷长时，必有e_ts（t）趋于零。因而，控制系统的稳态误差定义为误差信号e（t）的稳态分量e_ss（∞），常以e_ss简单标志。

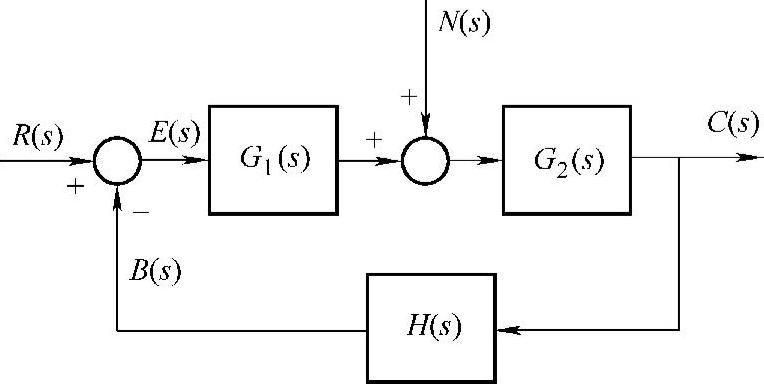
图7-9 典型控制系统

对于一个实际的控制系统，由于系统结构、输入作用的类型（控制量或者扰动量）、输入函数的形式（阶跃、斜坡或者加速度）不同，控制系统的稳态输出不可能在任何情况下都与输入量一致或者相当，也不可能在任何形式的扰动作用下都准确地恢复到原平衡位置，此外，控制系统中不可避免地存在摩擦、间隙、不灵敏区或零位输出等非线性因素，它们都会造成附加的稳态误差。因此，系统设计任务之一是尽量减小系统的稳态误差，或者使稳态误差小于某一容许值。

研究稳态误差有两种方法，即动态误差系数法和静态误差系数法。利用动态误差系数法，可以研究输入信号几乎为任意时间函数时的系统稳态误差变化，因此由这种方法得到的动态误差系数又称为广义误差系数。为了求取动态误差系数，改写式（7-20）为

E（s）=Φ_e（s）R（s） （7-23）

式中 Φ_e（s）——误差传递函数。

将误差传递函数Φ_e（s）在s=0的邻域内展成泰勒级数，于是，误差信号可以表示为

(www.xing528.com)

上述无穷级数收敛于s=0的邻域，称为误差级数，相当于在时间域内t→∞时成立。因此，当所有初始条件均为零时，对式（7-24）进行拉普拉斯反变换，就得到作为时间函数的稳态误差表达式为

式中，C_i——动态误差系数，。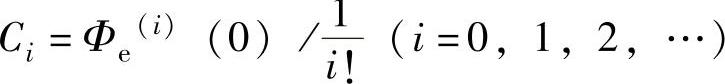

习惯上称C₀为动态位置误差系数，称C₁为动态速度误差系数，称C₂为动态加速误差系数。

一般情况下，伺服控制系统常用静态误差系数法来研究系统稳态误差。应当指出，在系统误差分析中，只有当输入信号是阶跃函数、斜坡函数和加速度函数，或者是这三种函数的线性组合时，静态误差系数才有意义。它的关系式如下：

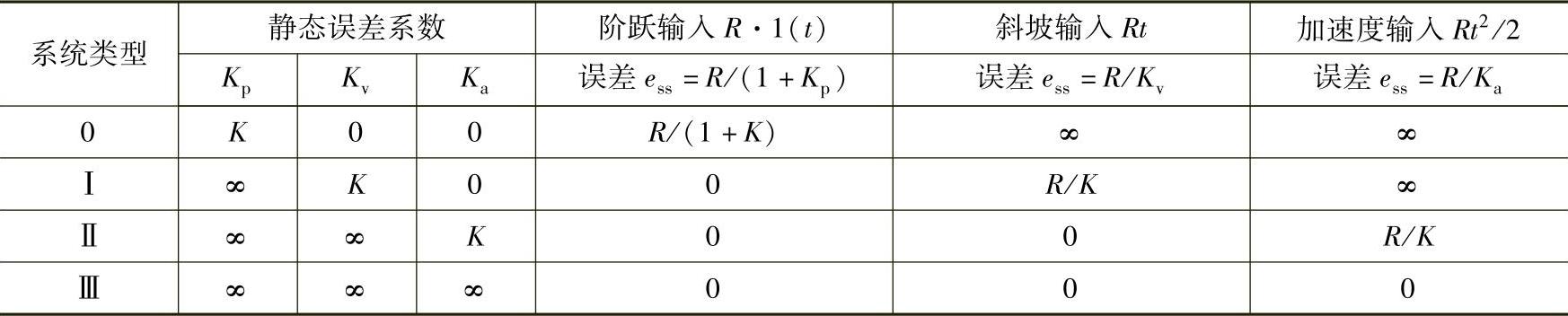
由于稳态误差是误差信号稳态分量e_ss（t）在t趋于无穷时的数值，上式实质是用终值定理法求得系统的终值误差。它不能反映e_ss（t）随时间t的变换规律，这一点具有一定的局限性，但是它比动态误差系数法容易得多。表7-1列出了不同的反馈控制系统类型在不同输入信号形式下的静态误差系数。同时从表中也可以看出，对于同一个控制系统，在不同形式的输入信号作用下具有不同的稳态误差。

表7-1 输入信号作用下的稳态误差

实际上，动态误差系数与静态误差系数之间存在一定的关系，在典型系统模型中，这种关系如下：

0型系统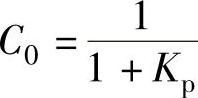：；Ⅰ型系统：；Ⅱ型系统：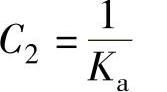

依据表7-1，如果系统存在稳态误差，为了减小或消除系统在输入信号和扰动作用下的稳态误差，通常采取的措施是：

①增大系统开环增益或者扰动作用点之前系统的前向通道增益；

②串联积分环节，改变系统类型。

特别需要指出的是，在反馈控制系统中，设置串联积分环节或者增大开环增益以消除或减小稳态误差的措施，必然导致系统稳定性的降低，甚至造成系统不稳定，从而恶化系统的动态性能。因此，权衡考虑系统稳定性、稳态误差和动态性能之间的关系，便成为系统环路设计的主要内容。