指令响应与扰动响应优化方案

指令信号是系统应该尽可能地进行跟随的系统输入，指令响应是用来量度一个系统如何迅速跟随指令信号。

在时间域里，量度指令响应最常用的是对一个阶跃信号响应的超调量和调节时间，如图7-6a所示。图中，超调量定义为在典型的阶跃响应跟随过程中，输出量超出稳态值的最大偏离量与稳态值之比，用百分数表示：

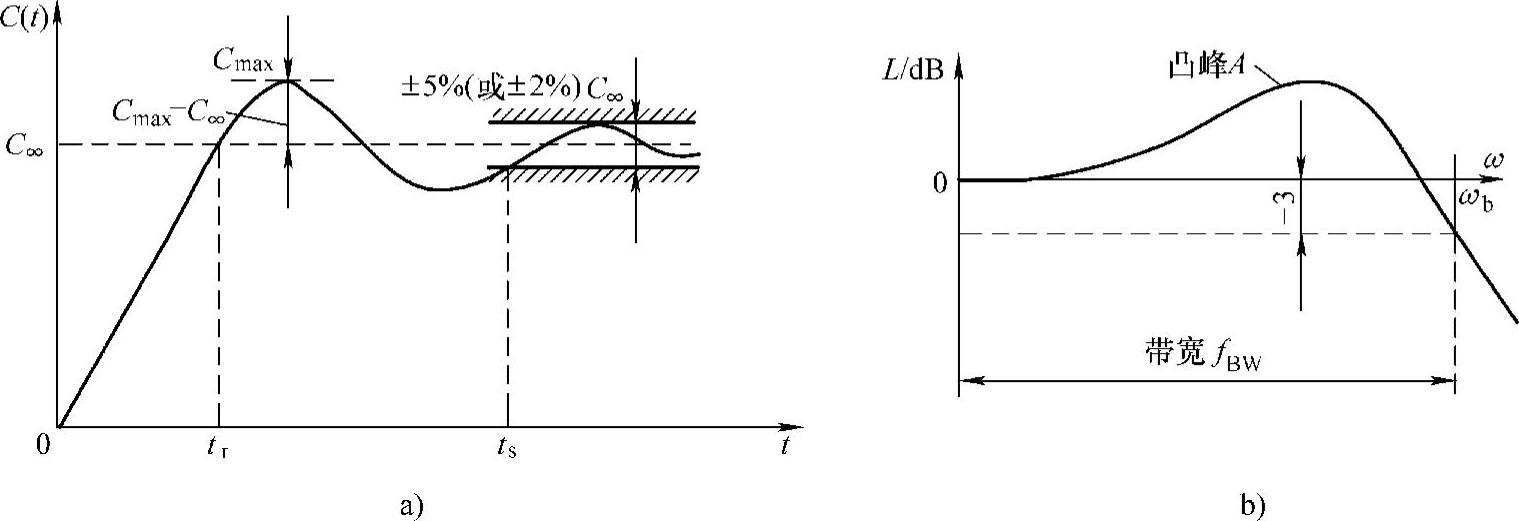
图7-6 典型阶跃指令响应性能指标

a）时间域指标 b）频率域指标

调节时间t_s也称过渡时间，它是用来衡量系统整个调节过程的快慢的。原则上它应该是从给定量阶跃变化起到输出量完全稳定下来为止的时间，对于线性控制系统来说，理论上要达到t=∞时，系统才真正稳定，但是实际系统由于存在非线性等因素并不是这样。因此，一般在阶跃响应曲线的稳态值附近，取某个范围作为允许误差带，以响应曲线达到并不再超出该误差带所需的最短时间，定义为调节时间。

例如，调节时间：

t_s=t₅% （7-12）

式中 t₅%——响应到达并保持在终值±5%内所需的最短时间。

t_s=t₂% （7-13）

式中 t₂%——响应到达并保持在终值±2%内所需的最短时间。

系统响应也可以在频域里通过观测增益来进行测量，如图7-6b所示。交流伺服控制系统可以证明，它们在低频响应速度快，但是在高频却响应迟钝。这意味着在低频时其增益将接近0dB，但随着频率继续增加，增益会不断下降，在高频段时，增益已经下降到非常低，远小于0dB。

闭环系统响应能力常用的量度是带宽，与带宽对应的那个频率f_BW的增益比原来下降了-3dB，或者幅值下降到原来的70%。另外一个度量是凸峰A，它是稳定性的一种量度。在图b中，低频处的增益为0dB，随着频率的增加，增益应该减小，如果在开始减小前增益增大了，表明是临界稳定，这种现象就是凸峰。从实际测量中得到，凸峰值的允许范围为0～4dB。

对于交流伺服控制系统，时间域量度与频域量度之间的关联性是明显的，调节时间对应于带宽，超调量对应于凸峰。超调量越大，凸峰就越明显，稳定性就越差；而调节时间越快，带宽就越宽，系统响应能力就越强。根据第2章“三相交流永磁同步电动机”2.3.2“机械时间常数、电气时间常数和机电时间常数”中所述，系统接收阶跃指令信号，响应信号趋于指令信号，当趋近在5%误差带时，即有e^-t/τ=5%，则t=3τ，而系统传递函数是一阶惯性环节，按定义，可知道系统带宽频率2πf_BW=1/τ，于是可得到调节时间与带宽之间有如下关系：

t₅%≈3/（f_BW×2π） （7-14）

同理类推，得到

t₂%≈4/（f_BW×2π） （7-15）

由式（7-14）或式（7-15）可知，调节时间和带宽成反比关系，为了说明其关系更具有普遍意义，可借助时域和频域的反比性质推导如下。图7-7中，两个系统M₁（s）和M₂（s）的频率曲线如图a，阶跃函数分别通过M₁（s）和M₂（s），得到阶跃响应函数h₁（t）和h₂（t），如图b所示。假定图a中两个系统在某频率处有如下关系：

(www.xing528.com)

式中 λ——任意常数。

对h₁（t）和h₂（t）进行拉普拉斯变换得到

考虑式（7-16），并应用拉普拉斯变换相似定理，即得

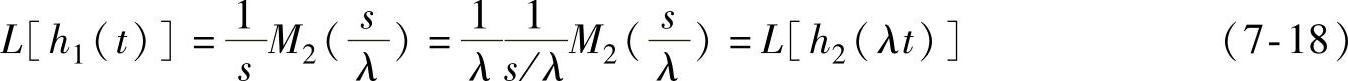
故

h₁（t）=h₂（λt） （7-19）

由式（7-16）推导出式（7-19），其含义为：系统的频率特性放宽几倍，单位阶跃响应就加快几倍。因此可得到带宽和调节时间的反比关系。

在系统正常运行中，虽然很少有阶跃指令信号，但是时间域量度的观测通常还是取决于阶跃响应，这是因为在一定范围内，阶跃响应与其他波形相比更容易被测量。然而，实际许多现象发生在多个频率的组合中，单从一个阶跃响应中收集对系统准确定量数据通常是不现实的。此外，有时用时域量度说明会更为困难。因此，频域量度使用相对会更广泛些。

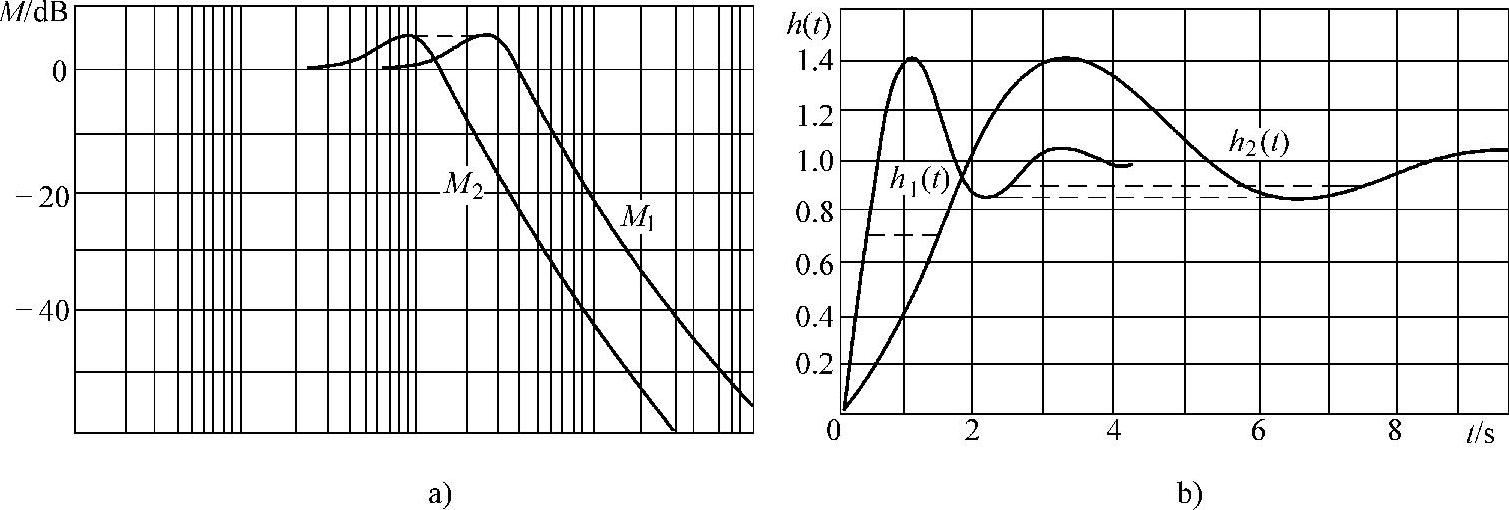
图7-7 带宽与调节时间的反比性质

扰动是控制系统应该被克服的输入。同指令信号相比，扰动更难于产生。因此，扰动响应测量起来比较困难。有时，扰动响应指的是它的反面，也就是抗扰动，或者与此等价的动态抗扰动能力。这两个可供选择的量度是控制系统中对同一个量的量度，它们给出了扰动响应的相互关联性：强扰动抑制力，却是低扰动响应的系统。

一般以系统稳定运行中突加一个使输出量降低的负扰动N以后的过渡过程作为典型的抗扰过程，如图7-8所示。扰动响应最常用的量度是动态降落ΔC_max和恢复时间t_v。很明显，动态降落ΔC_max即为信号跌落的最大差值。

从阶跃扰动作用开始，到输出量基本上恢复稳态，距新稳态值C_∞2之差进入基准量C_b的±5%（或者±2%）范围之内所需的时间，定义为恢复时间t_v。这里需要注意的是，C_b称为输出量的基准值，其值并非是C_∞2，这是因为动态降落本身就很小，倘若动态降落小于5%，则按进入±5%C_∞2范围来定义的恢复时间只能为零，就没有什么意义了。因此，C_b需要视具体情况选定。

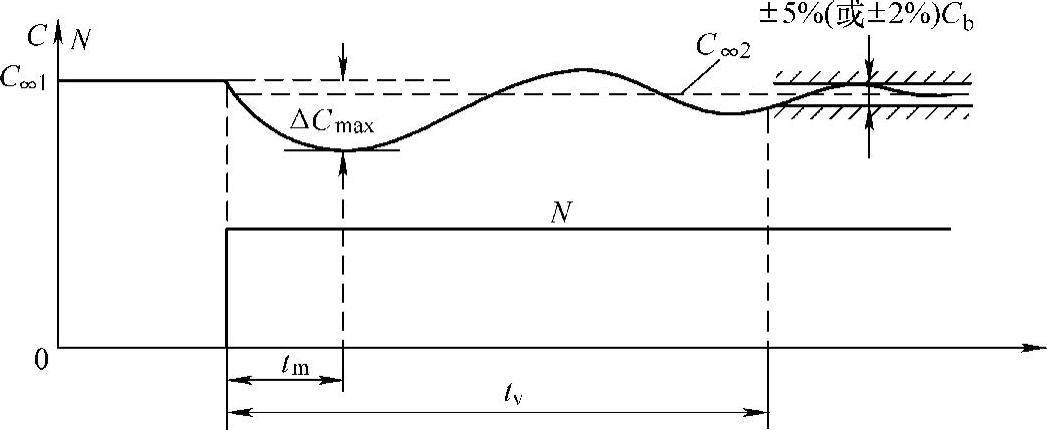
图7-8 突加扰动的动态过程和抗扰性能指标

ΔC_max—动态降落 C_∞1—原稳态值 C_∞2—新稳态值 t_v—恢复时间

实际中，控制系统对各种动态性能指标的要求各有不同。工业机器人和数控机床用的位置随动系统要有较严格的跟随性能；而连轧机是要求高抗扰性能的调速系统，至于转速的跟随性能，只希望没有超调，过渡过程慢些没有什么关系。总之，一般来说，调速系统的动态指标以抗扰性为主，而随动性系统的动态指标则以跟随性能为主。