典型系统的稳态准确度及稳定性分析

一般来说，系统的开环传递函数都可表示为

式中，分子和分母上都可能含有复数零点和复数极点诸项。分母中的s^r项表示系统在原点处有r重极点，或者说，系统含有r个积分环节。根据r=0，1，2，…不同值，分别称为0型、Ⅰ型、Ⅱ型、…系统。自动控制理论证明，0型系统在稳态时是有差的，而Ⅲ型和Ⅲ型以上的系统很难稳定。因此，通常为保证稳定性和一定的稳态准确度，多用Ⅰ型和Ⅱ型系统。

1.典型Ⅰ型系统

作为典型Ⅰ型系统，其开环传递函数选择为

它的闭环系统结构如图7-4a所示，图b表示它的开环对数频率特性。选择它作为典型系统不仅因为其机构简单，而且对数幅频特性的中频段以-20dB/dec的斜率穿越零分贝线。只要参数的选择能保证有足够的中频带宽度，系统就一定是稳定的，且有足够的稳定裕量。显然要做到这一点，应有

则相位稳定裕度有

γ=180°-90°-arctanω_cT＞45° （7-7）

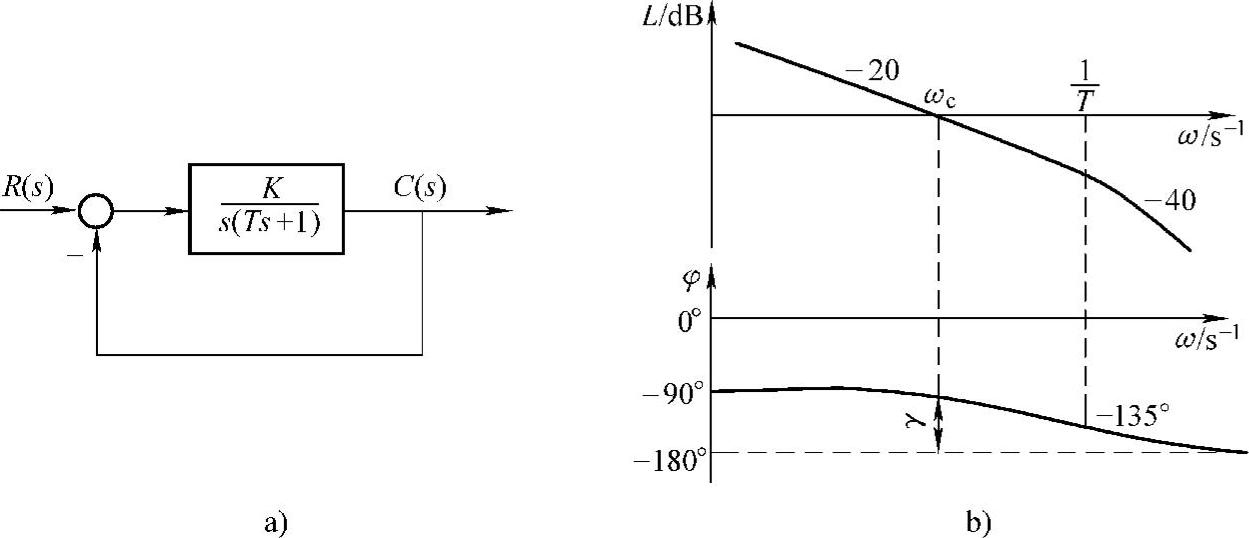
图7-4 典型Ⅰ型系统

a）闭环系统结构框图 b）开环对数频率特性(www.xing528.com)

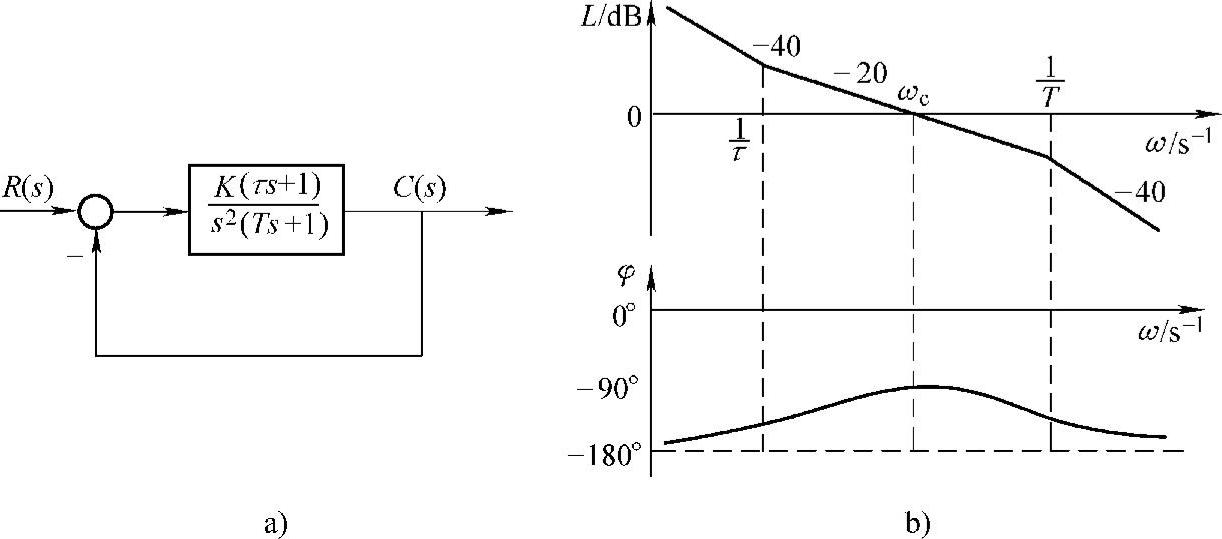
图7-5 典型Ⅱ型系统

a）闭环系统结构框图 b）开环对数频率特性

2.典型Ⅱ型系统

在Ⅱ型系统中，选择一种最简单而稳定的机构作为典型的Ⅱ型系统，其开环传递函数为

它的闭环系统结构和开环对数频率特性如图7-5所示，其中频段也是以-20dB/dec的斜率穿越零分贝线。由于分母中已经有s²，对应的相频特性是-180°，后面还有一个惯性环节（这是实际系统必定有的），如果在分子上不添加一个比例微分环节（τs+1），就无法把相频特性抬到-180°线以上去，也就无法保证系统稳定。要实现图b这样的特性，显然应有

则相位稳定裕度为

由上式可得到，τ比T大得越多，则稳定裕度越大。