转速估计与编码器分辨率优化技巧

光电编码器以量化离散的形式给出位置信息，微处理器通过这些离散位置值最终估计出转速。最简单的转速估计形式如下：

v_k=（p_k-p_k-1）/T （6-14）

它是通过有规则的间隔对位置进行采样，并在每个采样间隔采用简单差分的形式估计出转速的。我们最为熟悉的M法测速就是这种转速估计形式。由上式可以看出，用简单差分形式估计出的转速不仅带来了延时，而且估计准确度也受到了有限的编码器分辨率的影响。

编码器分辨率引起的误差可以通过一个简单的例子来解释。假设转速为每采样周期4.5线，每次采用周期内测量得到的位置增量总为整数，即5，4，5，4，…，转速估计误差值在每采样周期±0.5线振荡。±0.5线的误差，在高速的情况下是微不足道的，然而在低速时，误差值会变得较为重要，不能忽略。

显而易见，提高分辨率最直接的方法就是采用具有较高线数的编码器，但是在有时，它是不实际的或者是受客观因素（价格、安装空间等）限制的。于是，还可以通过采用一些方法提高分辨率，其中一种常用的方法就是M/T法，其公式为

v_k=（p_k-p_k-1）/（t_k-t_k-1） （6-15）

由上式可以看到，增强形式的转速估计方法不仅仅是在每个采样时间内对编码器的跃变进行简单的计数，它还通过准确测量编码器发生阶跃度的时间来提高分辨率。采用简单差分，时间测量的分辨率即是采样周期，或许有几百微秒左右；而对于M/T法而言，分辨率可以达到1μs，这是因为大多数带有集成定时器的微处理器都能以1μs或与之相当的准确度来测量时间。如图6-24所示，与实际v=4.5线/周期相比较（1周期=100μs，即0.045相比较），按式（6-14）和式（6-15）分别估计出转速为

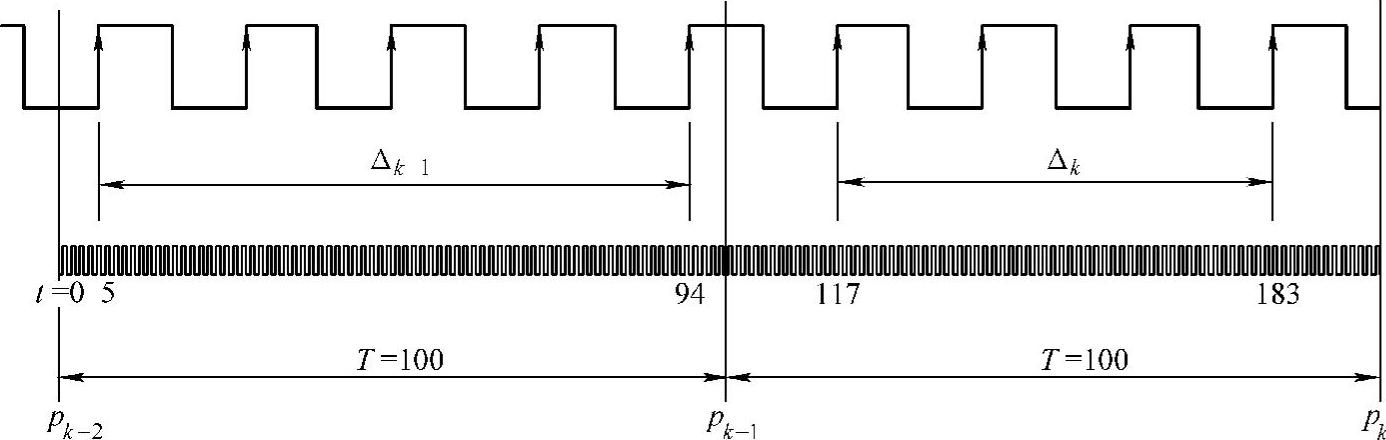
图6-24 v=4.5线/周期，时间采样频率为1MHz时的位置与时间关系

由此可见，M/T法不依赖于固定的采样时间，其优点是不增加相位滞后，特别是在电动机转速很慢时，同时它也提高了噪声的敏感性。由于传统经典的M/T法也存在不足之处，为此又出现了变M/T法等方法，以进一步改善M/T法的性能和实用性。(www.xing528.com)

无论采用M法还是M/T法，因为是由两个离散时刻的位置差值来估计转速的，都会引起分辨率噪声，导致电流尖峰的产生。为了减弱这些噪声，通常的方法是增加低通滤波器。这样的滤波器衰减了高频分量，因此消除了大多数有限分辨率带来的有害结果。很遗憾，这些滤波器同时也向内环引入了相位滞后，这些延时的影响在转速快速加减速变化时最为明显。一般地，分辨率越粗糙，需要的滤波器越苛刻，过多的延时会降低系统的稳定裕度，甚至会引起系统的不稳定。因而由分辨率与控制律增益之间的间接关系得到以下结论：

①有限分辨率需要使用低通滤波器进行消噪；

②低通滤波器在回路中引入了相位滞后；

③增大的相位滞后减小了稳定性裕度；

④较低的稳定性裕度迫使降低控制律增益。

因此，常常会看到：以提高有限的编码器分辨率为目的的转速估计方法都会借助简单差分形式建立如下所示的估计转速的多项式：

Δx_k=p_k-p_k-1

v_k=g₀Δx_k+g₁Δx_k-1+g₂Δx_k-2+…+g_m-1Δx_k-m+1 （6-17）

多项式中的每项系数g₀～g_m-1与数字滤波器中的系数密切联系，相关的研究结果将在第9章“数字滤波器”9.4“转速估计滤波器”中详细介绍。