Z变换和离散化方法详解

之前，我们研究了数字控制系统的采样和保持，那么再加上系统对象部分的传递函数，是否可以像连续系统那样用传递函数法来分析采样离散控制系统呢？回答是否定的，因为在采样系统的拉普拉斯变换式（5-3）中存在着s的超越函数e^Ts，这将使利用拉普拉斯反变换求解时域问题时变得十分麻烦。为了便于计算，就需要用z变换。

引进另一个复变量z，定义为

z=e^Ts （5-29）

或者

则式（5-3）可以改写成

式（5-31）就是x^∗（t）的z变换。其中字母Z表示取z变换，而字母z时表示复变量。由此可见，z变换是拉普拉斯变换的一种变形，因为z变换是针对采样时刻信息的，所以x^∗（t）的z变换就是x（kT），k=0、1、2、…时的z变换。通常把采样周期T当做一个单位，即T=1，于是记x（kT）为x（k）。这样采样序列的z变换可以定义为

将式（5-32）与式（5-2）相比可以看出，在采样序列z变换的级数形式中，x（k）表示脉冲序列的幅值，而z^-k则表示相应的幅值延迟了k个采样周期或者叫k拍。显然，z^-k是单位脉冲δ（t-kT）的z变换，即有

Z[δ（t-kT）]=z^-k （5-33）

或者

Z[δ（t）]=1 （5-34）

因此，对一个连续信号x（t）取z变换，只表示对这个函数在各个采样时刻0、T、2T、…的离散信号x^∗（t）取z变换。同样，如果求X（z）的反变换，得到的将是x^∗（t），而不是x（t）：

x^∗（t）=x（k）=Z^-1[X（z）] （5-35）

由此可见，z变换与s变换相比，在定义、性质和计算方法等方面，虽然有许多相似的地方，但是z变换也有其特殊规律。

1.z变换的多解性

z变换与采样序列x^∗（t）相对应，与原连续信号x（t）并非一一对应；与此类似，所求出的z反变换也不可能是唯一的。于是，对于连续时间函数而言，z变换和z反变换都不是惟一的，如图5-11所示，连续信号x₁（t）和x₂（t）的采样序列相同，即x^∗₁（t）=x^∗₂（t），则它们的z变换也是相等的，然而x₁（t）≠x₂（t）。因此，这种按式（5-29）标准变换，从s域到z域的多值对应关系很可能导致频率混叠现象，这是它的缺点。

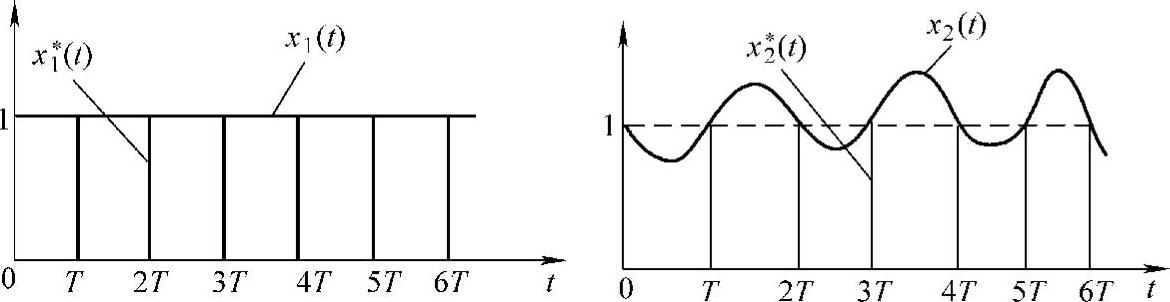
图5-11 具有相同z变换的两个连续时间函数

2.z变换的收敛性

对式（5-32）展开为

X（z）=x（0）+x（1）z^-1+x（2）z^-2+… （5-36）

它是复变量z^-1的一个幂级数，只有当其收敛时，即

存在，则z变换才存在。通常，大多数工程问题中的z变换都是存在的，因此对z变换的收敛区间不再特别指出。

实际上，式（5-2）按式（5-29）的z变换方法，又称为脉冲响应不变法。响应不变法的基本思想是依据系统的外特性，使离散时间系统在典型激励信号的作用下，其响应序列与连续时间系统在对应输入下响应的采样值相等，即y（kT）=y^∗（t）且t=kT（k=0，1，2，…）。依据典型输入的不同，可分为脉冲响应不变法（即上面所述的z变换法）、阶跃响应不变法和斜坡响应不变法等。在各种响应不变法中，重点考虑的是系统外特性的相似性，离散化均采用z变换，因此s域与z域有对应的稳定性关系。其中，脉冲响应不变法广泛地应用在各种数字系统的直接设计中。阶跃响应不变法保证了连续与离散的阶跃响应相同，由它得到的数字滤波器就是假定这些滤波器对阶跃指令具有与它们相对应的模拟滤波器相同的响应而得到的。由于z变换不易求取，斜坡响应不变法很少应用。

在响应不变法中，从s域到z域的多值对应关系会导致频率混叠现象，为了克服这一缺点，双线性变换法是一种性能较好的可选方法，它可使s域与z域保持单值映射关系，从而有效地克服了z变换中由于多值映射带来的频谱混叠问题，其典型应用在无限冲激响应（IIR）数字滤波器的设计中。双线性变换法可按式（5-29）用两个s域的线性函数的比值来逼近z。从z的定义开始：

(www.xing528.com)

e^Ts的泰勒级数为

用泰勒级数的前两项代入式（5-38），得到

对式（5-40）变换得到

式（5-41）能用来获得逼近任一s域函数的z域传递函数，并且不会产生频率混叠。式中左边把s带换成jω就是G（s）的频率特性；右边把z代换成e^jωT就是H（z）的频率特性。这两个频率特性函数相近但不相等。假设G（jω）在ω_A和H（e^jωT）在ω_D时，频率特性值相等，即：

G（jω_A）=H（e^jωD^T） （5-42）

代入式（5-41）有

最后得到

分析式（5-44），正切函数把s平面压缩在s₁平面中的-jπ/T≤jω≤jπ/T水平条带内，即图5-4中主频谱范围，则s₁平面与z平面建立的映射关系，即式（5-41）必然是一一对应关系，且不发生混叠。双线性变换法正是源于复频域中的二次映射的方法有效地解决了z变换带来的多值映射问题。

由式（5-44）发现，双线性变换后，频率特性相等的点上频率ω_A和ω_D并不相等（ω=0除外）。对于数字滤波器设计来说，如果单纯地做双线性变换，则所得的数字滤波器的频率特性将发生畸变，甚至连截止频率都相差甚远。图5-12以一个低通滤波器为例表示这种非线性频率畸变。

图5-12 双线性变换的非线性频率畸变

图5-12中左上部是模拟滤波器的频率特性，右下部是数字滤波器的频率特性，在频率轴方向被非线性地压缩了，与模拟滤波器差别较大。其实，脉冲响应不变法并没有这种频率特性的非线性畸变，如果不发生频谱混叠，则得到的数字滤波器与模拟滤波器的频率特性基本相同。在这一点上，脉冲响应不变法反而优于双线性变换法。

为了使数字滤波器的幅频特性在截止频率ω₀上与已知的模拟滤波器相同，需要对双线性变换进行修正。修正后双线性变换的好处是可以用来确保相位与增益在某一频率处有等效性。这在特定频率期望严格等效的场合下（例如陷波滤波器）是非常有用的。按式（5-44），式（5-41）可修改为

式中 ω₀——期望严格等效的频率。

参照式（5-43）推导过程，式（5-45）逆推得到

因此，当ω=ω₀时，因数相对消，只剩下s的确切值：s=jω₀，这意味着当传递函数在期望弯曲频率处估算时，这种近似是严格准确的。

最后，本节还需要再提到一种变换方法，即差分变换方法。它源自数值积分思想，按后差方式和前差方式，s与z的关系式分别为

前差变换法，由于式（5-48）不能保证变换前后有对应的稳定性关系，在数字系统中很少采用；而后差变换法，因为式（5-47）变换简单，且当T很小时，性能也较好，因此常用在对已有模拟系统的离散化实现中，具体内容请参看第8章“控制器”8.2“PID控制器实现”所述内容。

综上所述，z变换方法的实质是传递函数由s域到z域的等效。“等效”是指在时域特性、频率特性和稳态增益等方面的相近。不同离散方法所具有的特性不同，并且接近程度也不一致。因此，必须要了解不同方法的特点，并且确定出哪种特性是最重要的，以此来选择合适的z变换方法。