量化误差与极限环分析

在数字控制系统中，量化是一个值得注意的实际问题。量化是数字控制系统的一种非线性效应，它来源于传感器的局限分辨率，量化过程导致了量化误差和极限环。如果传感器的分辨率足够精细，量化过程的影响就可以忽略。

1.量化误差

连续信号x（t）经过一定位数A-D转换器的量化（不考虑采样过程）后变成x^∗（t），其误差定义为

式中 x^∗（t）——量化前的采样信号；

（t）——量化后的采样信号；

e——量化误差，可取0～q之间的任意值，q为量化单位。

量化结果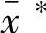（t）有两种处理方式，即“有舍有入”和“只舍不入”。“只舍不入”是把结果的小于q的部分置为0；“有舍有入”类似四舍五入，把结果小于0.5q的部分置为0，大于等于0.5q的部分置为1。可见，这两种量化特性曲线都为阶梯状，为非线性特性。

下面对其特性进行分析，由于e在0～q之间机会均等，因而是在[0，q]区间上均匀分布的随机变量，这种随机变量称为量化噪声。因为是随机变量，因而量化误差或者量化噪声需要用概率论的方法进行分析，其中主要包括数学期望E（e）和标准差σ（又称均方差）：

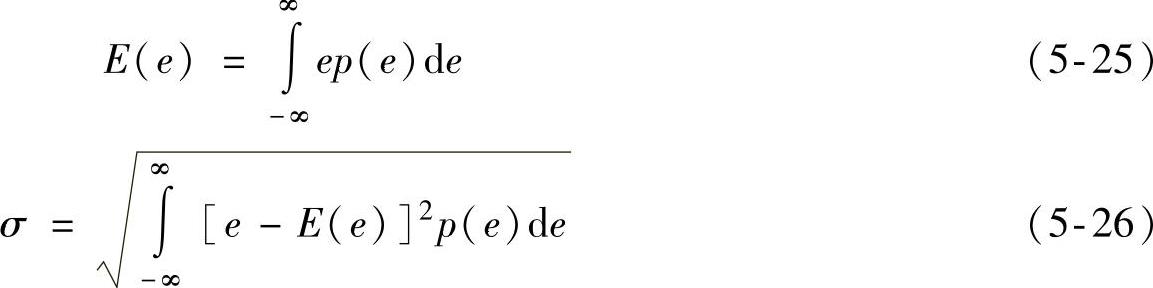
式中 p（e）——概率密度。

图5-8给出了两种量化结果的概率密度，结合式（5-25）和式（5-26）可计算出它们的量化特性，见表5-1。由表比较可知，它们的标准差相同，但“有舍有入”法最大误差小，且是无偏的。所以绝大部分A-D转换器采用的都是“有舍有入”方式。

表5-1 两种量化过程的误差分析

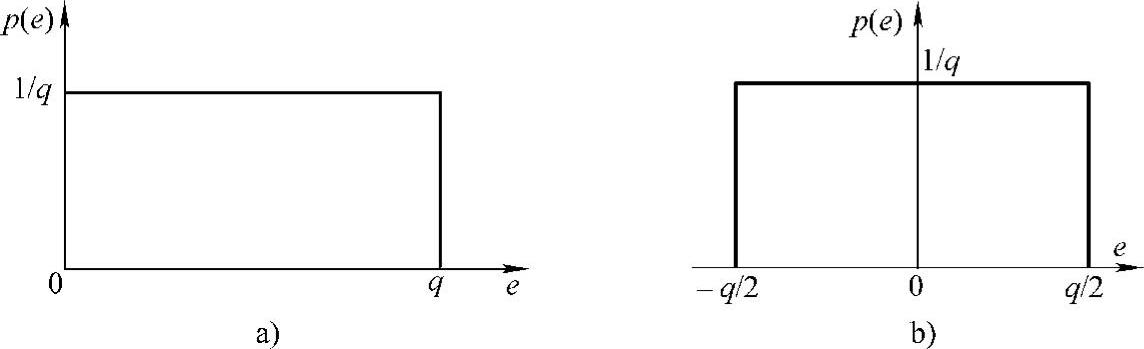
图5-8 两种量化方法的概率密度

a）“只舍不入”法 b）“有舍有入”法

为了减小量化误差e，应尽量减小量化单位q。q的计算方法为(www.xing528.com)

式中 x_max——模拟信号最大值；

x_min——模拟信号最小值；

i——字长；

m——级数或层数。

由式（5-27）可见，（x_max-x_min）是一定的，i决定着q，如图5-9所示。当i短q大时，量化过程产生低频大幅度量化噪声；而当i长q小时，量化过程产生高频小幅度量化噪声其量化噪声。x（t）变化迅速，噪声频率加快。

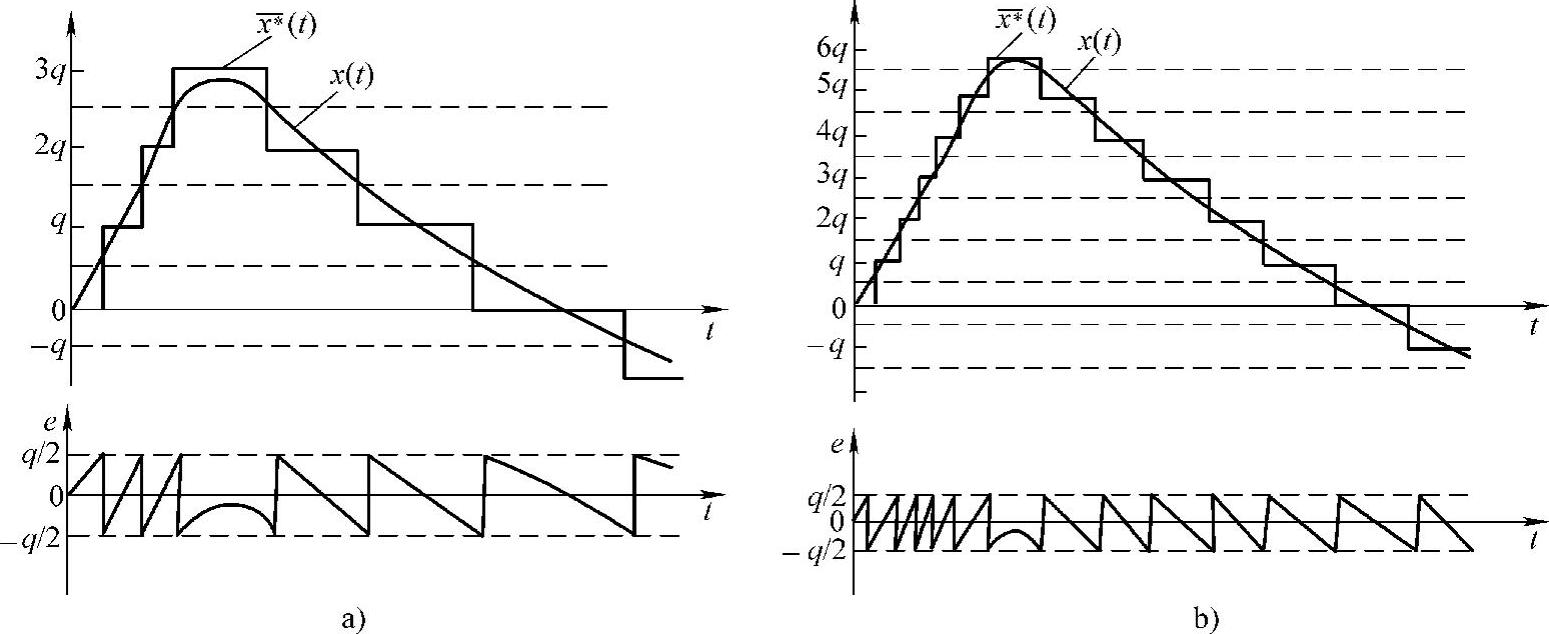
图5-9 量化噪声曲线

a）i短 b）i长

上述两种情况的量化噪声夹杂在输入信号中进入数字控制器，并随计算程序传递到输出量中，使数字控制系统输出信号中也含有噪声分量，从而导致输出不平滑。通常，系统具有低通滤波特性，可以抑制高频噪声，但较难抑制低频噪声。因此，数字控制器的字长不宜太短，除采用数字滤波器外，A-D转换器的字长i要在最大限度上尽可能地选择较大。

2.极限环

量化的另一种影响称为极限环，它是非线性系统特有的特征。在相平面上，一个极限环定义为一个独立的闭曲线，如图5-10所示。轨线必须是闭合的，而且是独立的。当时间t→∞时，极限环附近的所有轨线收敛于这个极限环，则称为稳定极限环；当时间t→∞时，轨线逐渐远离极限环，则称为不稳定极限环；当时间t→∞时，某些轨线逐渐收敛于极限环，而另一些轨线偏离极限环，则称为半稳定极限环。

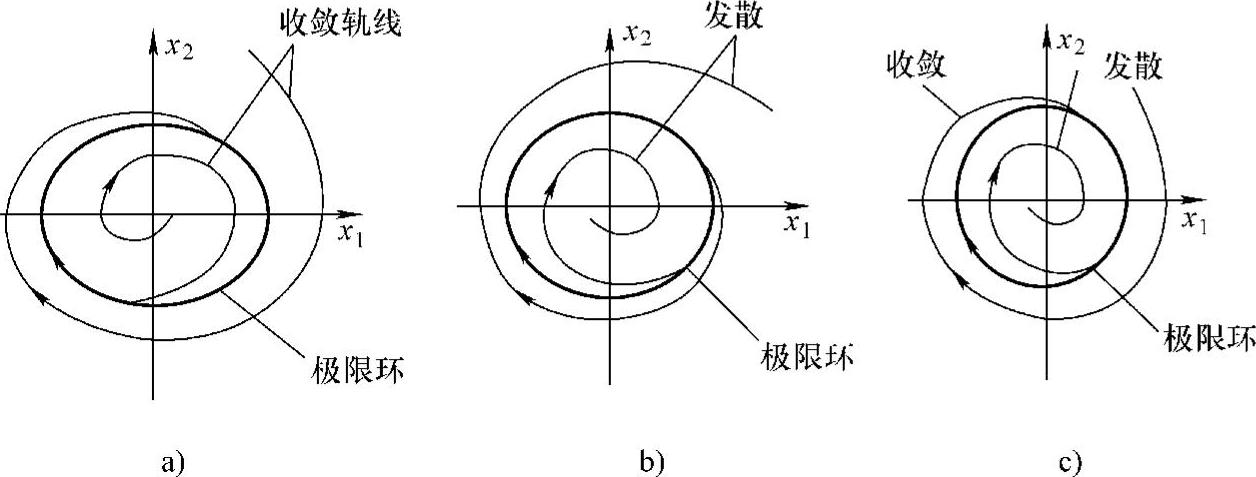
图5-10 极限环轨迹

a）稳定极限环 b）不稳定极限环 c）半稳定极限环

在数字计算中，极限环是由量化误差引起的低强度振荡。虽然它可以产生持续的振动，振荡频率低，幅值比量化单位q大许多倍，但它是稳定极限环。有两种方法可以减小极限环的幅值。一种方法是提高运算的分辨率，即选择浮点运算或者增长整型数学运算的字长。另一种方法是引入抖动，即在输入信号上叠加一连续变化的信号。抖动实质是提高了A-D转换过程的信噪比，或者说是提高了A-D的分辨率，从而大大减小极限环振动的幅值，甚至可以忽略极限环。因此，抖动信号是抑制极限环幅值的关键。然而，实际上抖动信号的选择往往凭借更多的是经验而不是理论，关于抖动信号的具体例子请看第6章“传感器技术和检测数据处理”6.4.1节“过采样和A-D分辨率”中所述。