信号复现及零阶保持器技术分析

数字控制器一个周期计算一次并输出，该输出通常保存在D-A（数字-模拟）转换器中，然后保持恒定直到下一个周期。采样（输出到D-A）与保持（在一个周期内保持为常量）功能在模拟系统中是没有的，但是存在于所有的数字系统中。

采样后，在由离散信号向连续信号的转换过程中，保持器需要解决的问题是：在kT与（k+1）T时刻之间，即当0＜Δt＜T时，连续信号x（kT+Δt）与x（kT）的关系如何？从数学上说，保持器的任务是解决各采样点之间的插值问题。

实际上，保持器是具有外推功能的器件。保持器的外推作用，表现为现在时刻的输出信号取决于过去时刻离散信号的外推。通常，采用如下多项式外推公式描述保持器：

x（kT+Δt）=a₀+a₁Δt+a₂（Δt）²+…+a_m（Δt）m （5-9）

式中 Δt——以kT时刻为原点的坐标。

式（5-9）表示，现在时刻的输出x（kT+Δt）取决于Δt=0、-T、-2T、…、-mT各过去时刻的离散信号x^∗（kT）、x^∗[（k-1）T]、…、x^∗[（n-m）T]的（m+1）个值。外推公式中（m+1）个待定系数a_i（i=0，1，…，m），惟一地由过去采样时刻（m+1）个离散信号值x^∗[（n-i）T]（i=0，1，…，m）来确定，故系数a_i有惟一解。这样的保持器称为m阶保持器。若取m=0，则称为零阶保持器；m=1，称为一阶保持器。

由式（5-9）可以得到零阶保持器的外推公式为

x（kT+Δt）=a₀ （5-10）

显然，Δt=0时，上式也成立，所以有a₀=x（kT），从而零阶保持器的数学表达式为

x（kT+Δt）=x（kT）（0≤Δt＜T） （5-11）

上式说明，零阶保持器是一种常值外推的保持器，它把采样时刻kT的采样值恒定不变地保持（外推）到（k+1）T时刻，这样保持器把离散信号恢复成了一个阶梯形的连续信号x_h（t），如图5-5所示。x_h（t）的数学描述可以写成

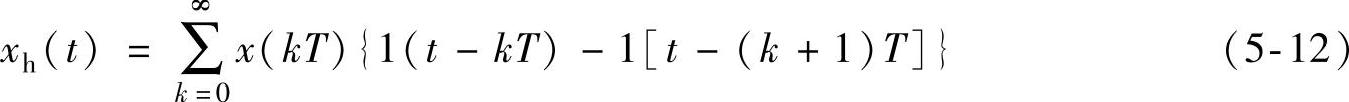
它的拉普拉斯变换为

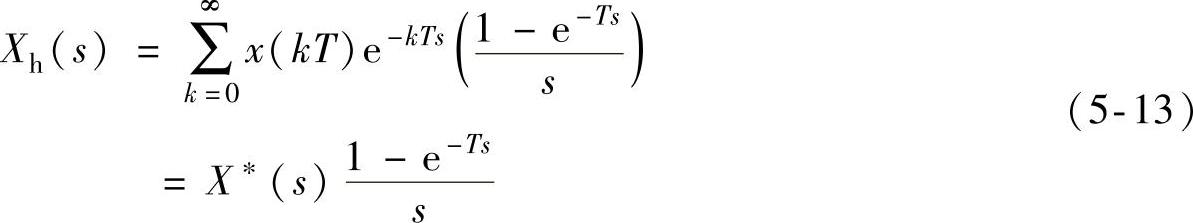
由此得到零阶保持器的传递函数为

将s=jω代入式（5-14），得到零阶保持器的幅频特性为

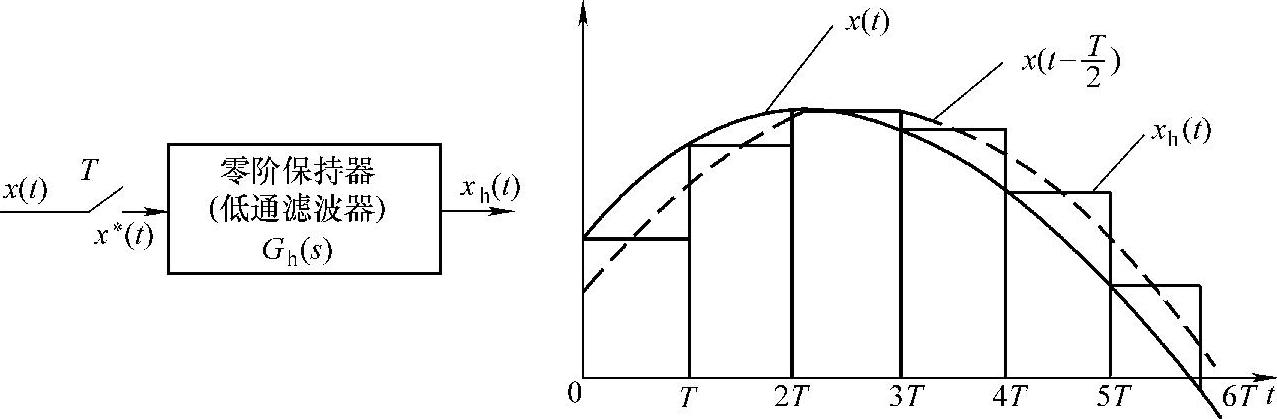
图5-5 采样和零阶保持前后的信号

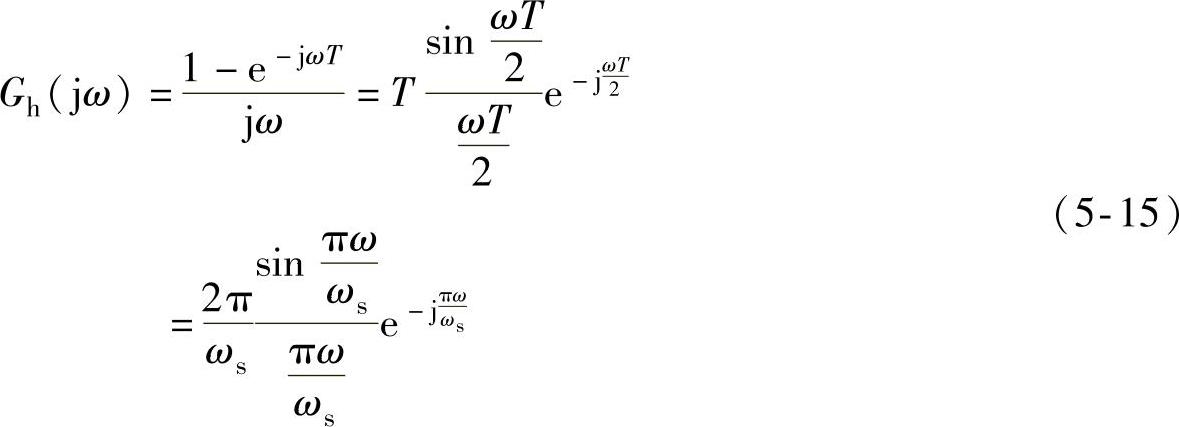
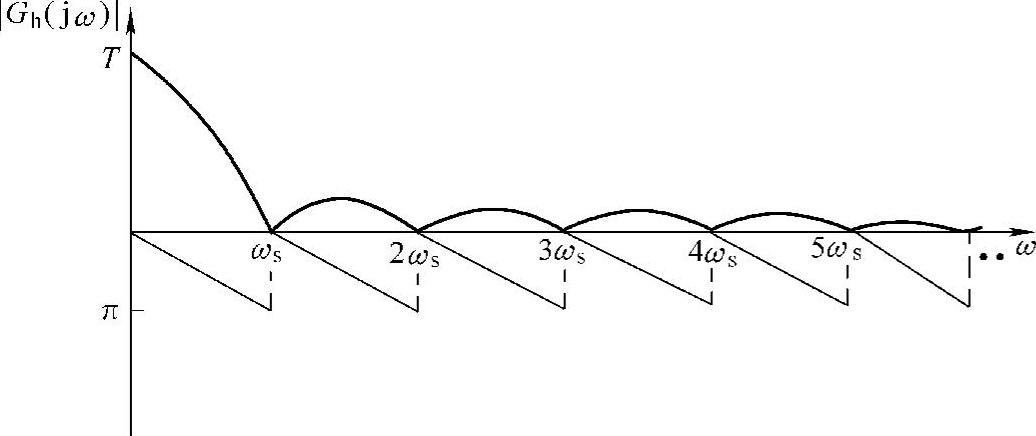
式（5-15）的幅频特性曲线如图5-6所示，零阶保持器的幅度随着频率的增高而逐渐减小，这说明它确实是一个低通滤波器，具有低通滤波特性，可以除去离散信号中的高频分量，而保留其有用的低频成分。但它并不是一个理想的低通滤波器，有多个截止频率，高频分量仍然能通过一部分，从而造成数字控制系统的输出中存在纹波。

(www.xing528.com)

图5-6 零阶保持器的幅频特性

同时，信号通过零阶保持器之后，保持输出恒定的结果是引入了相位滞后。因为输出是从上一次保存时间开始的，到这个间隔的末尾，输出滞后了整整一个周期。但是，在整个间隔内，从平均意义上来说，数据滞后了半个周期，如图5-5的虚线所示，x_h（t）比x（t）平均滞后了T/2。采样周期T越大，滞后越大，相当于引入一个纯滞后环节，这对闭环系统的稳定性是不利的。

对于一阶保持器，其外推公式为

x（kT+Δt）=a₀+a₁Δt （5-16）

将Δt=0和Δt=-T代入上式，可得到

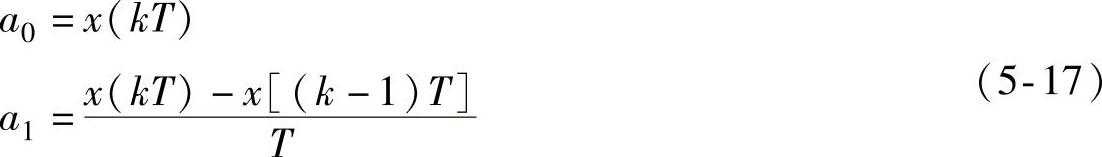
从而一阶保持器的数学表达式为

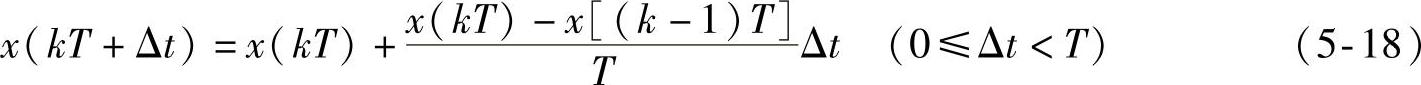
式（5-18）表明，一阶保持器是一种按线性外推得到的保持器，其输出特性如图5-7所示。类似的方法导出一阶保持器的传递函数和幅频特性：

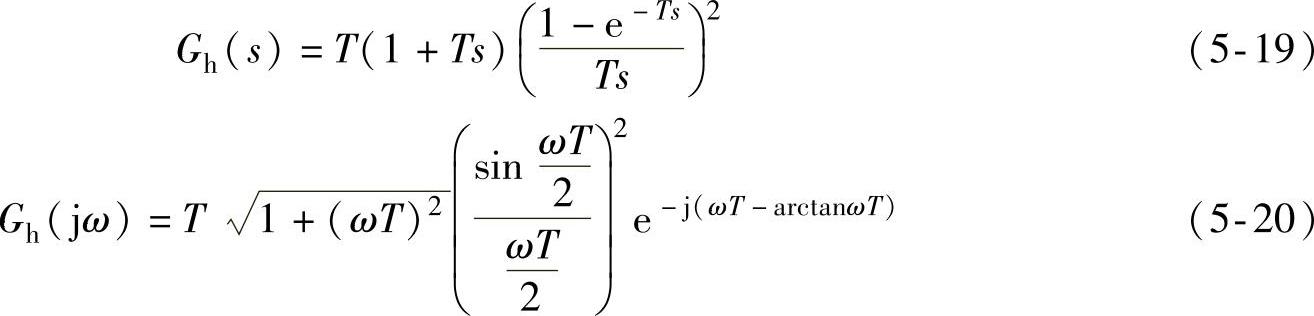
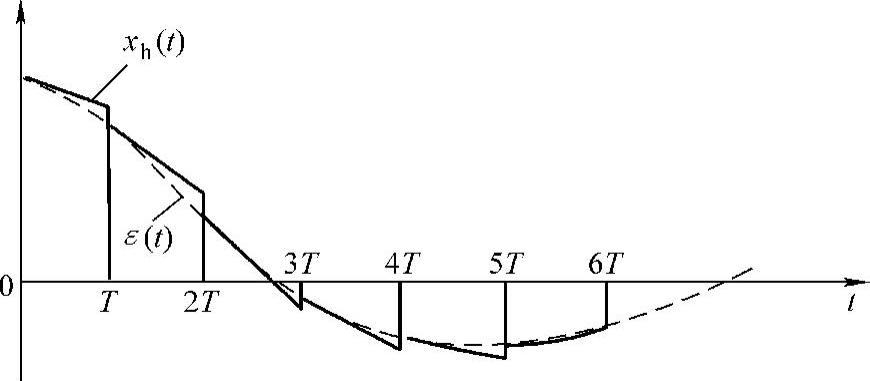
图5-7 一阶保持器的输出特性

与零阶保持器相比，一阶保持器复现原信号的准确度较高。对比式（5-15）和式（5-20），一阶保持器的幅频特性普遍较高，允许通过的信号高频分量较多，更容易造成纹波；此外，它的相角滞后比零阶保持器大，对系统的稳定性更加不利。因此，由于一阶或高阶保持器的原理和实现都比较复杂，在控制系统中很少采用，而普遍采用零阶保持器。虽然采用零阶保持器后得到的复现信号与原有信号比较不是毫无畸变的，只是由于系统中的被控对象一般都具有低通滤波特性，这种畸变对输出的影响就不会很严重了。

在大多数控制系统中，零阶保持器可以用R-C无源网络实现，一般隐含在D-A转换器中。因此，D-A的模型包括两部分：一个以V/bit为单位的常数K和一个零阶保持器G_h（S）。D-A的传递函数为

G_D-A（s）=KG_h（s） （5-21）

为方便分析，对于零阶保持器的传递函数，一个非常好的近似为

G_h（s）≈Te^-Ts/2 （5-22）

其频率特性为

对比式（5-23）和式（5-15）两个表达式，无论是在准确式（5-15）中还是在近似式（5-23）中，都具有相同的相位滞后（-ωT/2rad），但增益不同。式（5-23）的增益系数恒为1，然而式（5-15）的增益系数是sync函数，即sin（ωT/2）/（ωT/2），它在大多数所关心的频率范围内，其值接近1。例如在1/4采样频率（ω=2π/4T），sync函数的估算值为0.9，或者说是-1dB，它是如此接近0dB，以致其差别可被忽略。由于系统的带宽远低于采样频率，也就是低于采样频率的1/10，所以讨论系统在高频的准确增益也就没有什么意义。至于在奈奎斯特频率（1/2采样频率），这是系统可以处理的最高频率，sync函数的估算值为0.637，或者说-4dB，也是可以忽略的值。因此，这就是在大多数控制系统中，采用近似式（5-23）已经足够准确的原因。