逆变电路输出波形中所含谐波的多少是衡量PWM控制方法优劣的基本标志,但不是唯一的标志。提高逆变电路的直流电压利用率、减少开关次数也是很重要的。
1.调制度的定义与直流电压利用率
PWM最大调制度决定着直流电压利用率。定义PWM的调制度MI为

式中 U∗———相电压参考值。
下面,依据调制度的定义来分析六拍阶梯方式、SPWM方式和SVPWM方式的直流电压利用率。由式(4-24)可以看出,在六拍阶梯波方式下,由式(4-9)得到

在SPWM方式下,由式(4-16)推导出U∗=Ud/2,则

而在SVPWM方式下,由式(4-23)推导出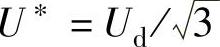 (正六边形内切圆半径),则
(正六边形内切圆半径),则

比较式(4-25)、式(4-26)、式(4-27)得出:六拍阶梯波方式MI最大,即电压利用率最高,SPWM方式MI最小,则它的电压利用率最低,SVPWM方式MI在两种方式之间,它的直流电压利用率是SPWM电压利用率的函数为换句话说,SVPWM直流电压利用率比SPWM高了15%。
2.过调制度
电压利用率在某些应用场合(例如弱磁升速)影响是非常大的,基于普通的SVPWM调制策略虽然已经有较高的电压利用率,但并不能达到最大。一般情况下,过调制增大了输出电压,从而进一步提高电压利用率。通常将调制区域分为连续调制区域Ⅰ和过调制区域Ⅱ和Ⅲ,如图4-18所示。SVPWM调制区域由合成电压空间矢量U∗轨迹决定:当U∗的轨迹为圆形且幅值不超出六边形内切圆时,调制区域是连续的,图中表示为调制度区域Ⅰ;当U∗处于内切圆和外接圆之间,图中表示为调制度区域Ⅱ,U∗的幅值受到限制,轨迹也不再是连续的圆形,可以通过过调制策略使得其幅值达到要求;外接圆以外的区域图中表示为调制度区域Ⅲ,它是不能达到的,一般采用的就是“六拍方式”,即U∗只沿着六边形的6个顶点进行旋转。

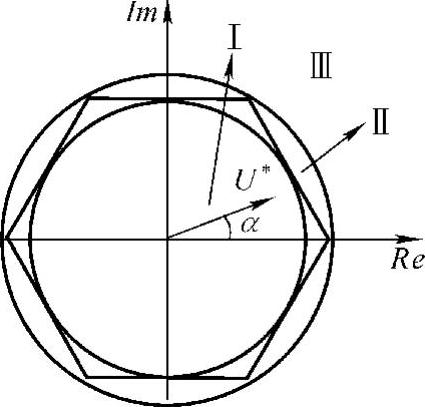
图4-18 SVPWM调制度区域示意图
基于图中调制度区域Ⅱ,学者提出了过调制策略,目前主要有两种实现方案:幅值跟随和相角跟随。所谓幅值跟随就是追求幅值的最大化,在相角上会与指令值有些差异;而相角跟随则是保证与指令电压相同的相角,但是在幅值上存在偏差。两种方式在过调制区域时,都采用了不同的调制函数,新的调制函数使基波幅值增大成为可能。相角跟随获得的过调制范围在0.906<MI≤0.952,而幅值跟随获得的过调制范围在0.952<MI≤1.0。
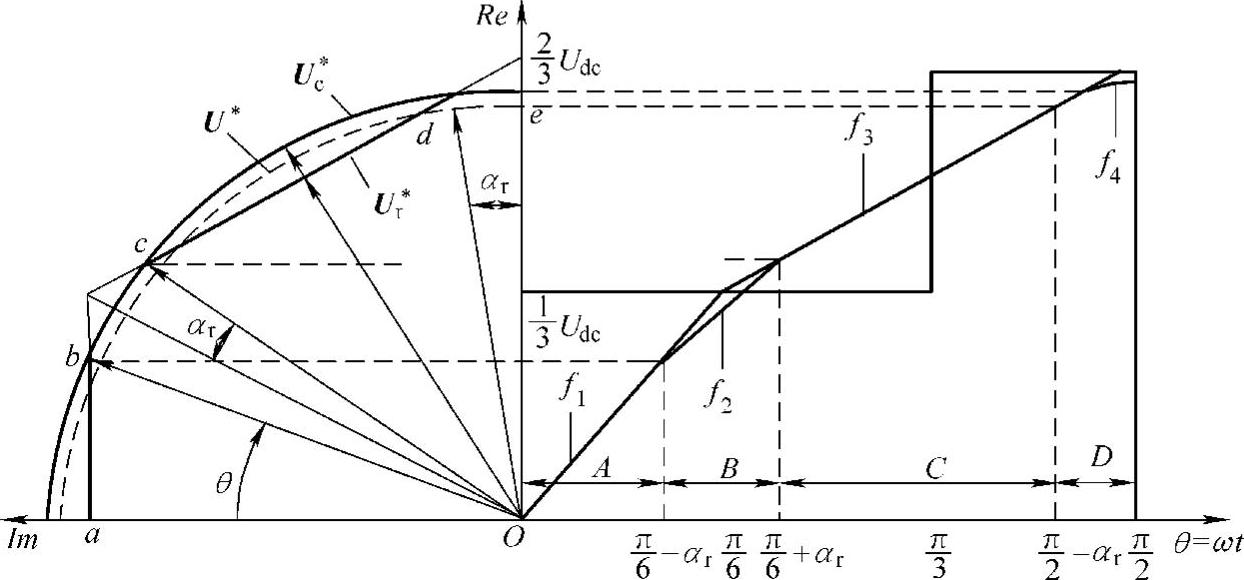
图4-19 相角跟随调制策略和相电压波形
图4-19给出了相角跟随调制策略和相电压波形。图中,U∗进入调制度区域Ⅱ,与六边形相交,如图中虚线所示,六边形把以U∗为半径的圆轨迹分成A、B、C、D段。由于受到物理限制,电压值是达不到A段和C段的,电压矢量最大只能落在六边形上。相角跟随过调制策略是在A段和C段补偿幅值,但是相角不变化,等效补偿后的电压幅值为U∗c,如图中实线所示。假定按图中θ=ωt方向由0到π/2旋转,αr由U∗c与六边形的交点确定,于是调制后实际的电压轨迹应为A段(ab直线),B段(bc弧线),C段(cd直线)和D段(de弧线),每段对应的相电压波形函数依次为f1,f2,f3和f4。
每段的相电压方程可写为
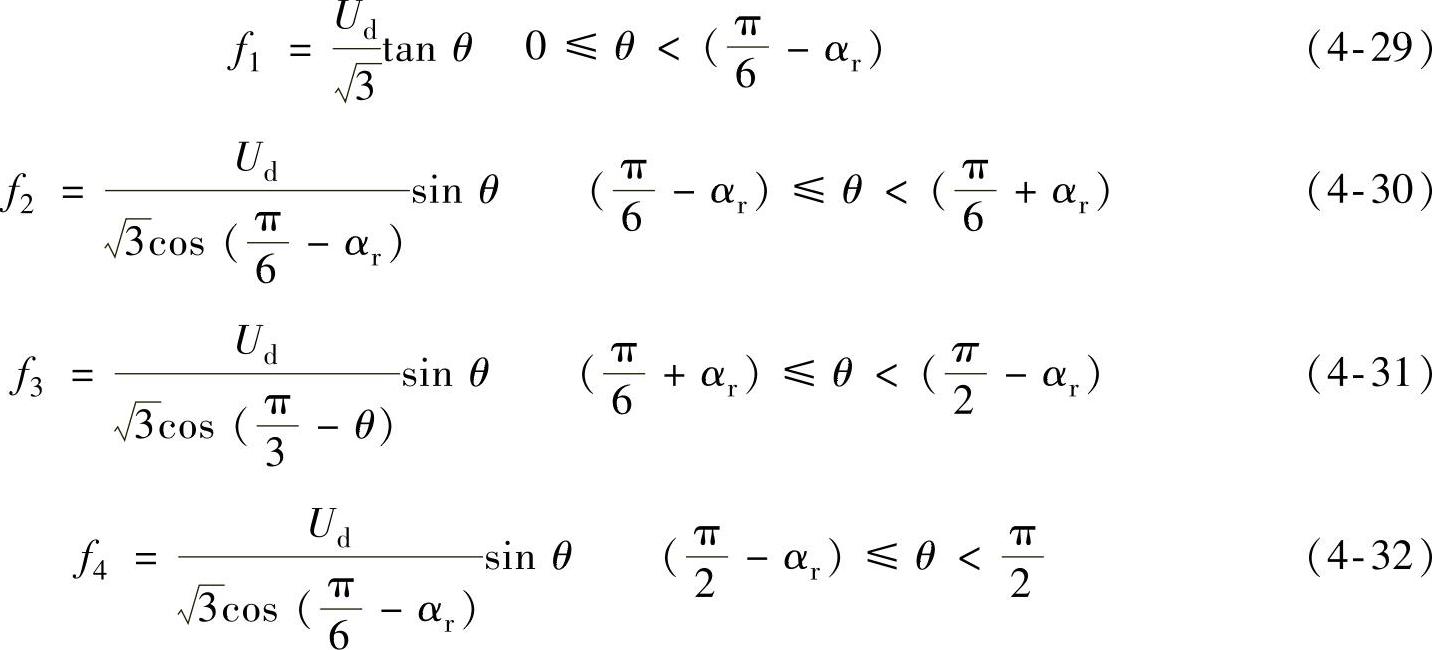
式(4-29)~式(4-32)中,0≤αr≤π/6。
因此,按式(4-6)得到相角跟随策略下的基波幅值函数为
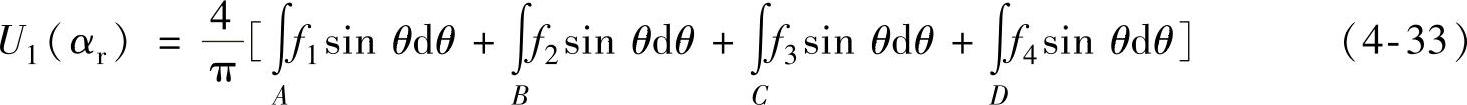 (https://www.xing528.com)
(https://www.xing528.com)
再由式(4-24)可得

于是得出MI与αr的关系如图4-20所示。
图4-21给出了幅值跟随调制策略和相电压波形。图中,U∗进入调制度区域Ⅱ,与六边形相交,如图中虚线所示,六边形把以U∗为半径的圆轨迹分成A、B、C、D段。幅值跟随过调制策略是在整个过程中追求幅值最大化,这样相角相应要发生变化。在A段,U∗幅值受限制后,为了保持幅值不降低,相应补偿后为U∗r,此时相角发生了变化,对应的关系为
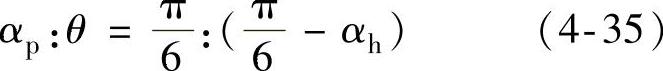
在B段时,电压幅值需要继续维持最大,即Ud/3,来补偿限制部分的消弱幅值,整段过程中,相角都指向点f处。C段过程类似A段,D段过程类似B段,于是,调制后实际的电压轨迹应为A段(ab直线),B段(bc弧线),C段(cd直线)和D段(de弧线),每段对应的相电压波形函数依次为f1,f2,f3和f4。
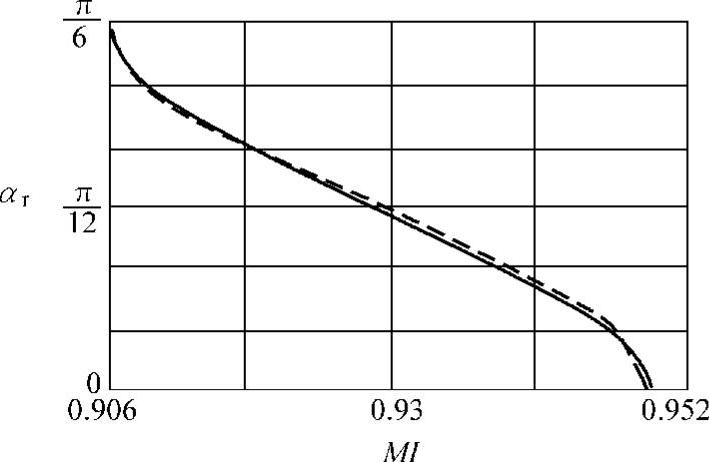
图4-20 相角跟随策略:αr与MI关系
每段的相电压方程可写为
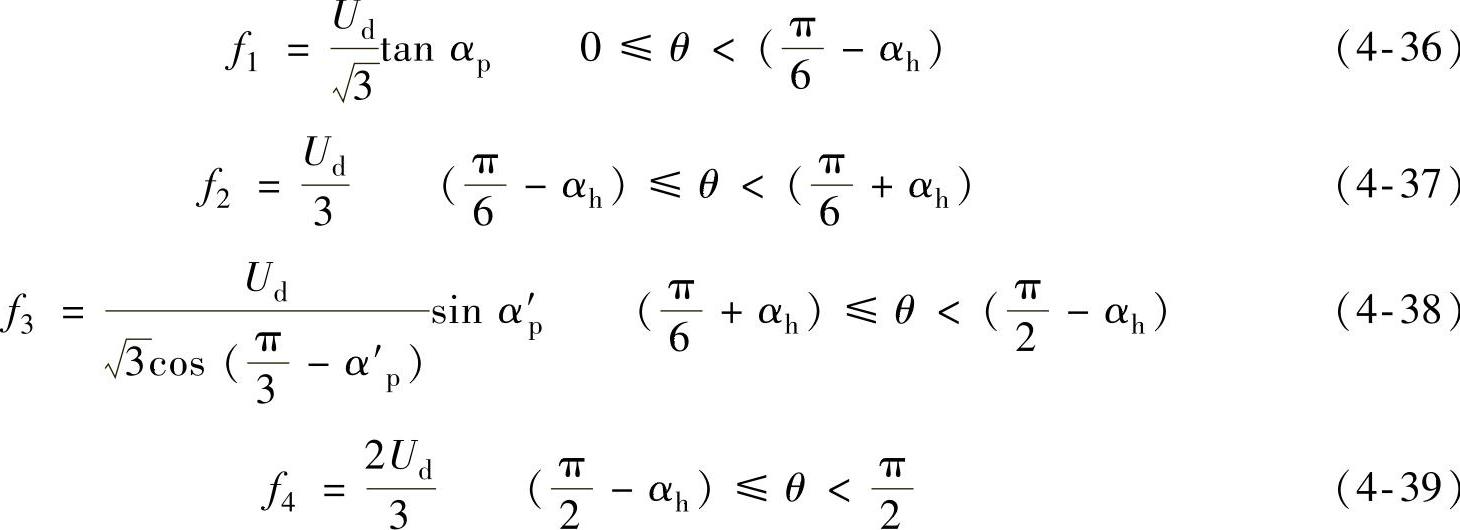
式(4-36)~式(4-39)中:
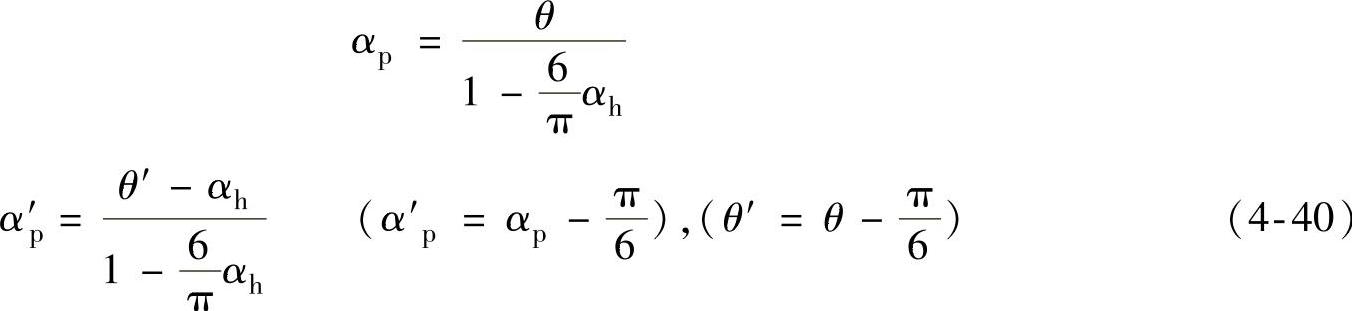
因此,按式(4-6)得到幅值跟随策略下的调制函数的基波幅值函数为
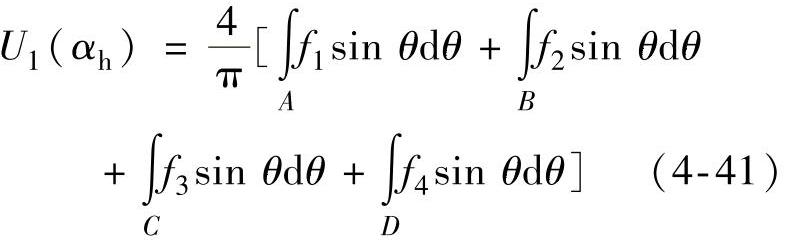
由式(4-24)可得
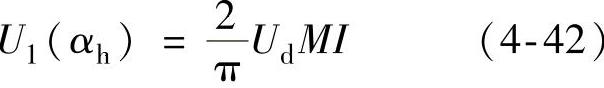
于是得出MI与αh的关系如图4-22所示。
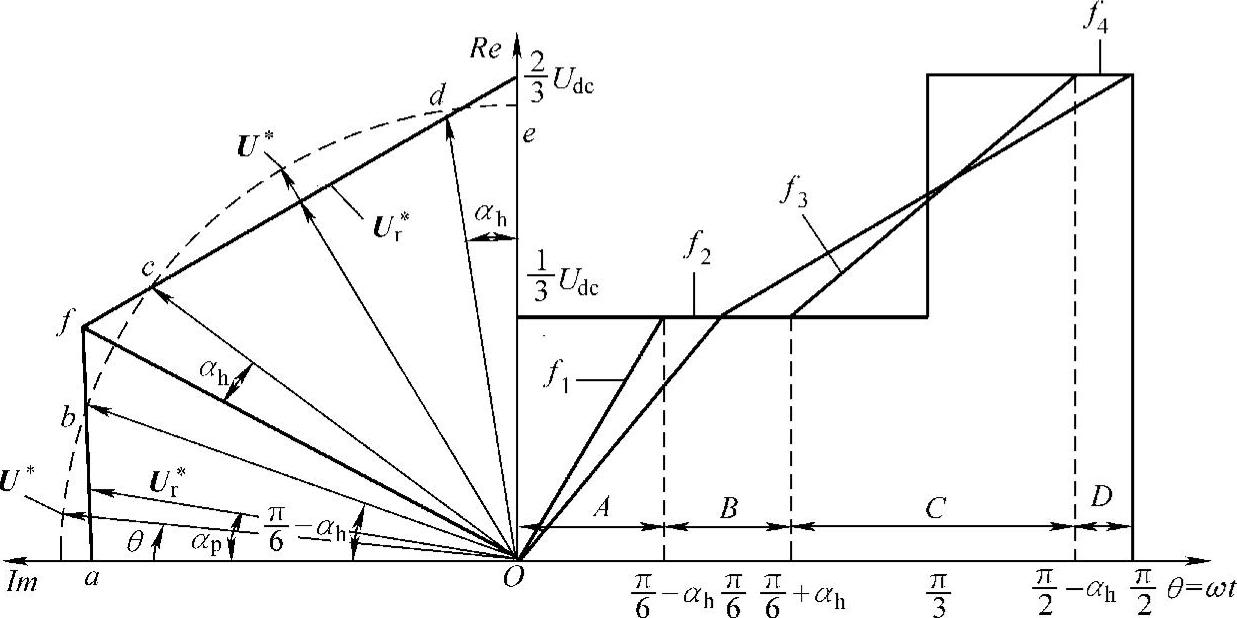
图4-21 幅值跟随调制策略和相电压波形
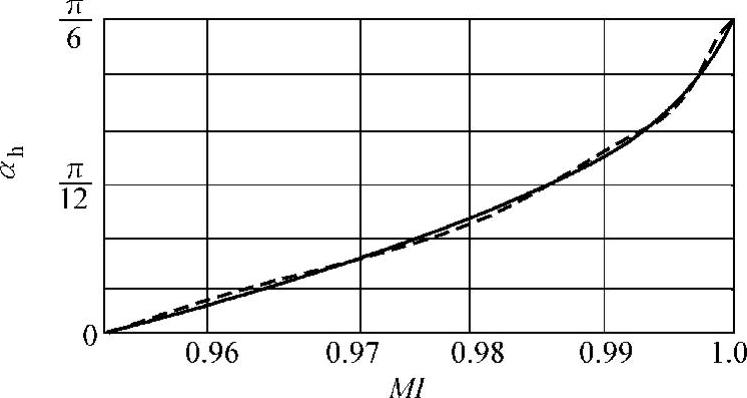
图4-22 幅值跟随策略:αh与MI关系
由此可见,过调制策略提高了电压利用率,同时使平均电压空间矢量不再是圆形轨迹,波形发生了畸变。图4-23给出了过调制下的电压谐波频谱。从图中容易看出,过调制策略引起的谐波影响还是令人满意的,尤其是在0.906<MI≤0.952范围内。
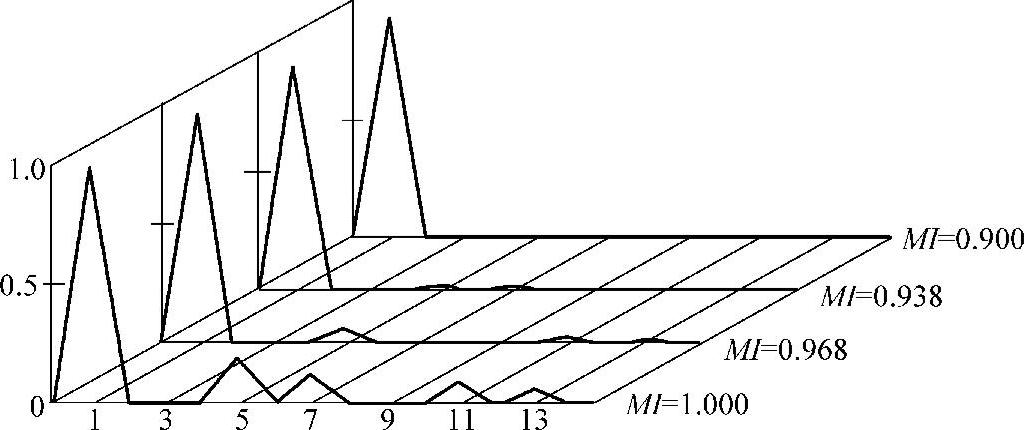
图4-23 过调制下的电压谐波频谱
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




