在采样控制理论中有一个重要的结论:冲量相等但形状不同的窄脉冲加在具有惯性的环节上时,其效果基本相同。冲量即指窄脉冲的面积,所说的效果基本相同,是指环节的输出响应波形基本相同。例如,图4-1给出了三个形状不同的窄脉冲,分别为矩形脉冲(图a),三角形脉冲(图b)和正弦半波脉冲(图c),但是它们的面积(即冲量)都等于1,那么当它们分别加在具有惯性的同一个环节上时,其输出响应基本相同。于是,当窄脉冲变为(图d)的单位脉冲函数δ(t)时,环节的响应即为该环节的脉冲过渡函数。
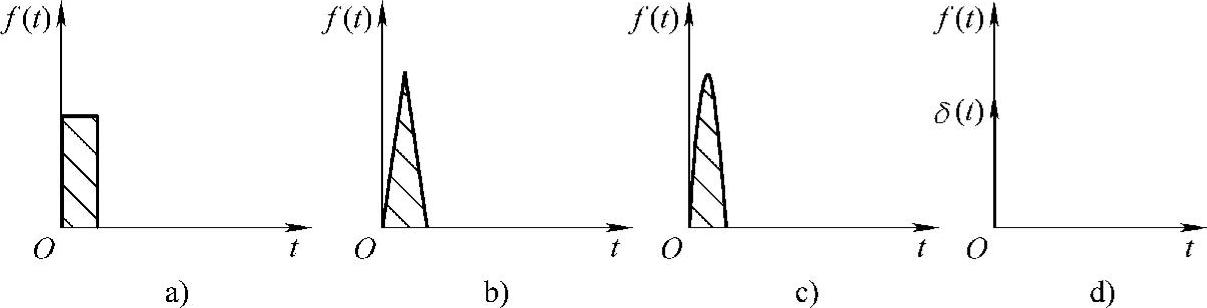
图4-1 形状不同而冲量相同的各种窄脉冲
a)矩形脉冲 b)三角形脉冲 c)正弦半波脉冲 d)单位脉冲函数
一个具有惯性环节的电路如图4-2a所示。图中,f(t)为电路的输入,它是一个电压窄脉冲,其形状和面积分别为图4-1的a、b、c、d,电路负载是一个R-L电路,产生电流i(t)为电路的输出。图4-2b给出了不同窄脉冲时i(t)的响应波形。从波形可以看出,在i(t)的上升段,脉冲形状不同时产生的电流形状也略有不同,但是其下降段则几乎完全相同。脉冲越窄,各i(t)波形的差异也越小。若周期性地施加上述脉冲,则响应i(t)也是周期性的。如果把各输出波形用傅里叶变换展开,则各i(t)在低频段的特性将非常近似,仅在高频段有所不同。
上述原理称为面积等效原理,它是PWM控制技术的重要理论基础。下面分析如何用一系列等幅不等宽的脉冲来代替一个正弦半波。将图4-3a所示的正弦半波分成N等份,因此正弦半波可以看成是由N个彼此相连的脉冲序列组成的波形。这些脉冲宽度相等,都等于π/N,但是幅值不等,且脉冲顶部不是水平直线,而是曲线,各脉冲的幅值按正弦规律变化。如果把上述脉冲序列利用相同数量的等幅而不等宽的矩形脉冲代替,使矩形脉冲的中点和相应正弦波部分的中点重合,且使矩形脉冲和相应的正弦部分面积相等,就得到图b所示的脉冲序列,这就是PWM波形。可以看出,PWM波形中各脉冲的幅值相等,而宽度是按正弦规律变化的。根据面积等效原理,PWM波形和正弦半波是等效的。要改变等效输出正弦波的幅值时,只要按照同一比例系数改变上述各脉冲的宽度即可。
像这种脉冲的宽度按正弦规律变化,并且和正弦波等效的PWM波形,也称为SPWM(Sinusoidal PWM)波形。除此之外,PWM波形还可以等效成其他所需要的波形,如等效成梯形波等,其基本原理也是基于等效面积原理。(https://www.xing528.com)
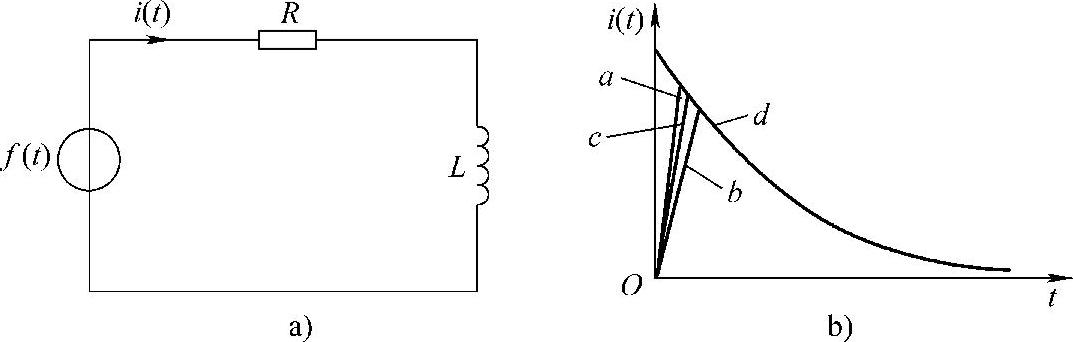
图4-2 冲量相同的各种窄脉冲的响应波形
a)具有惯性环节的电路 b)不同窄脉冲时i(t)的响应波形
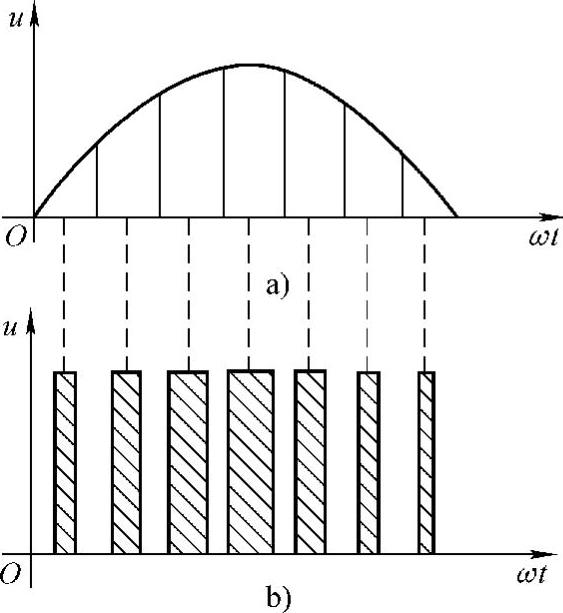
图4-3 用PWM波代替正弦半波
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




