矢量控制策略的优化方法

在具体的应用场合，永磁同步电动机矢量控制策略根据不同的速度调节范围、性能要求，可以分为如下形式：

①i_d=0控制；

②最大转矩/电流比控制；

③弱磁控制等。

下面主要阐述矢量控制策略中常用的这几种控制方法。

1.i_d=0控制

i_d=0控制即当永磁同步电动机定子电流的直轴分量在控制过程中始终等于0。由式（2-20）简化整理得到

直轴电流等于0，相当于等效直轴绕组开路不起作用。因此，如果不考虑定子直轴电压分量，仅仅从交轴电压方程可以看出：永磁同步电动机相当于一台他励直流电动机，定子电枢绕组只有交轴电流分量；励磁磁链等于转子永磁体产生的磁链，并且大小恒定不变；等效交轴绕组中的励磁电动势与转子角速度成正比。因为定子磁动势空间矢量与转子永磁体磁场空间矢量相互垂直，所以电磁转矩与交轴电流成正比，由式（2-32）简化得到

T^∗_e=p_nψ_ri^∗_q （2-69）

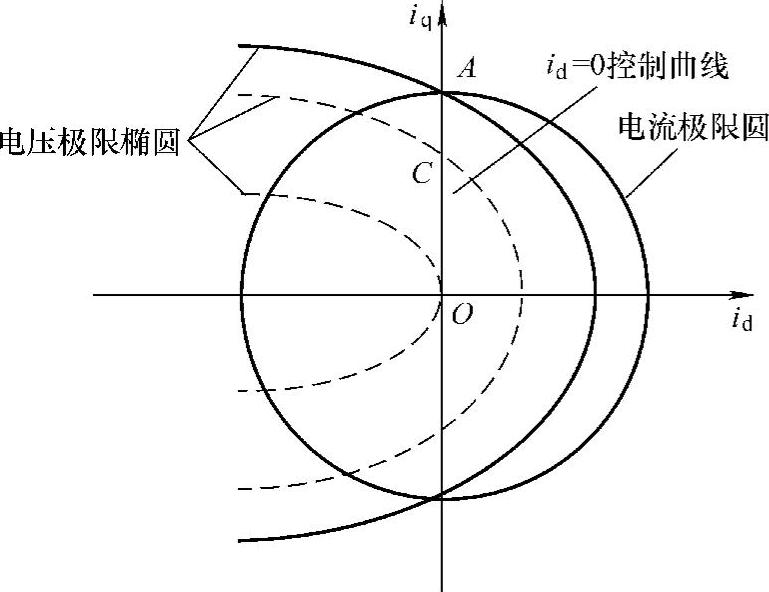
图2-15 电流极限曲线与i_d=0控制曲线

仅当i_q增大到i_max时，电磁转矩达到最大值，电动机在恒定的最大电磁转矩下，转速由零加速到额定值，反电动势也相应增大，在转速达到额定值后，其值接近电压限幅值。根据事先设计好的电动机参数，此时电压极限椭圆与电流极限圆的交点会在q轴上，且在电流极限圆q轴顶点的A位置，如图2-15所示。

由式（2-63）和式（2-69）可以得到A点位置的电动机角速度和转矩为

T_A=p_nψ_ri_max （2-71）

当转速超出额定值并继续升速时，电压极限椭圆要向内缩小，因而在该控制策略下，电流矢量轨迹只能是由A沿q轴向坐标原点移动，移动到原点时，转矩接近为零。此时该转速所对应的电压极限椭圆长轴经过原点，可求得原点的电动机角速度为

比较式（2-70）和（2-72）可知，电动机角速度由式（2-70）上升到式（2-72），升速范围较窄，同时在升速过程中转矩下降明显，将接近为零。因此，对于永磁同步电动机来说，采用i_d=0控制，电动机转速适合在额定转速范围内运行。因控制方法仅用变量i_q控制电磁转矩，其控制策略算法简单，控制灵活，因此在永磁同步电动机伺服系统中广泛应用。

2.最大转矩/电流比控制

i_d=0控制简单，但存在两个缺点：一方面是单位电流电磁转矩不是最大，另一方面是电动机只适合额定转速以下工作。最大转矩/电流比控制策略也称为单位电流电磁转矩最大控制策略，它能够控制电动机在单位电流下电磁转矩最大，且可以升速运行。因而它也是永磁同步电动机常用的控制策略之一，主要针对凸极电动机。

在什么条件下可以使单位电枢电流产生的电磁转矩最大？为了便于分析，在式（2-32）中引入电枢电流空间矢量与直轴位置的相位角γ，也就是定子磁动势幅值位置与转子直轴位置之间的交角，这时定子电流的两个分量与空间矢量幅值之间的关系为

将式（2-73）代入式（2-32）得到

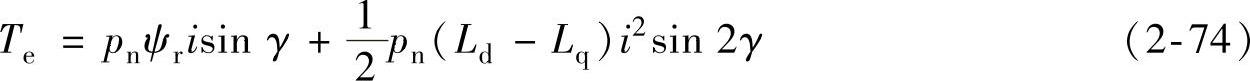
根据式（2-74），可以确定单位电流电磁转矩关于电流相位角的函数关系为

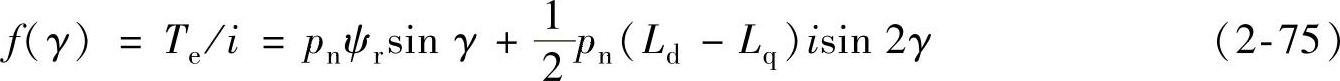
对式（2-75）求最大值，令γ的偏微分等于0，即әf（γ）/әγ=0，得到

ψ_rcosγ+（L_d-L_q）icos2γ=0 （2-76）

由式（2-76）可以得到

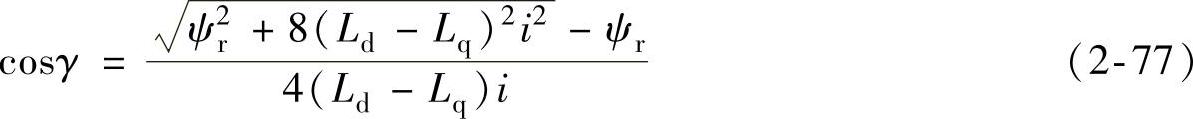
于是，满足单位电流电磁转矩最大条件下的定子电流直轴分量可以表示为

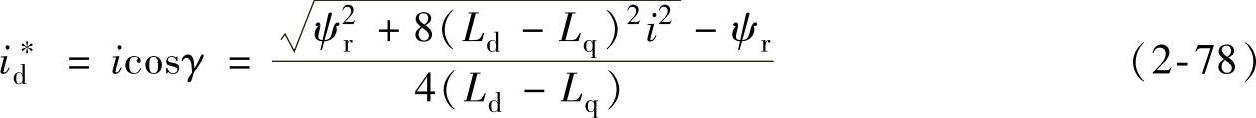
进一步推导，对式（2-76）两边同乘以i，并考虑式（2-73）的关系，经过整理后得到

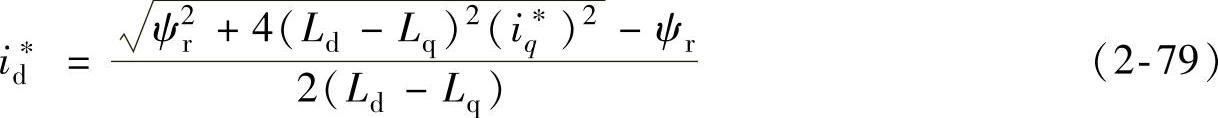
由该式可以分析得出，当L_d＜L_q，直轴电流小于0，电枢反应起去磁作用，当电动机转速超过额定转速时，这种控制策略因为能削弱转子磁场，称为弱磁控制方式，它可以扩大调速范围。当L_d＞L_q，直轴电流大于0，电枢反应起助磁作用，当电动机转速超过额定转速时，这种控制策略因为要增强转子磁场，因此无法作为电动机运行。

将式（2-79）代入式（2-32），得到单位电流电磁转矩最大条件下电磁转矩与交轴电流分量的关系为

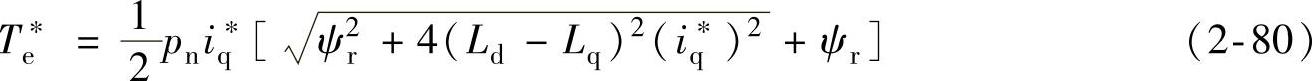
在单位电流电磁转矩最大控制策略实现过程中，由式（2-79）可以画出单位电流电磁转矩最大控制策略的最优控制曲线，如图2-16所示。图中，最优控制曲线（L_d＜L_q的情况）即是图2-13中最大转矩/电流轨迹。永磁同步电动机设计成功以后，最大电压极限曲线就确定了。如果最大电压极限曲线包含i_d=0控制策略的电流极限值点A点，那么i_d=0的控制策略可以达到额定转速。同理，如果最大电压极限曲线包含单位电流电磁转矩最大控制策略的电流极限值点B，那么单位电流电磁转矩最大控制策略可以达到额定转速。而且，单位电流电磁转矩最大控制策略能在最大恒转矩条件下达到更高转速。即当永磁同步电动机的电流极限曲线、电压极限曲线和最优控制曲线三者相交于同一点（B点）时，对应转速就是单位电流电磁转矩的最大控制在最大恒转矩负载下能达到的转速。

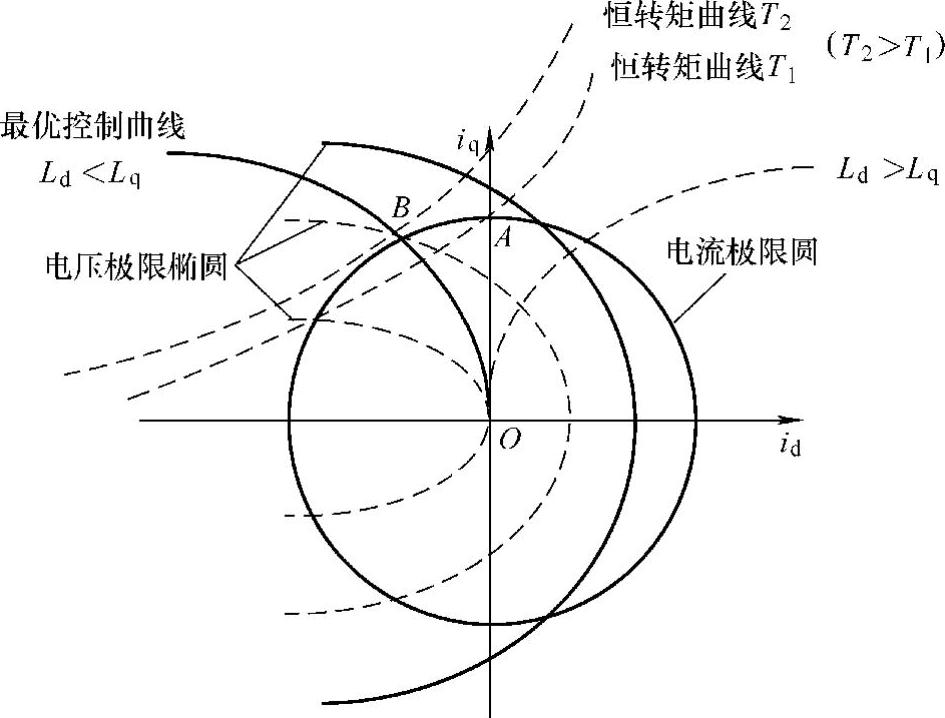
图2-16 电流极限曲线与最优控制曲线

因此，由式（2-79）和式（2-64）可以推导出与B点对应的直轴和交轴电流分量为

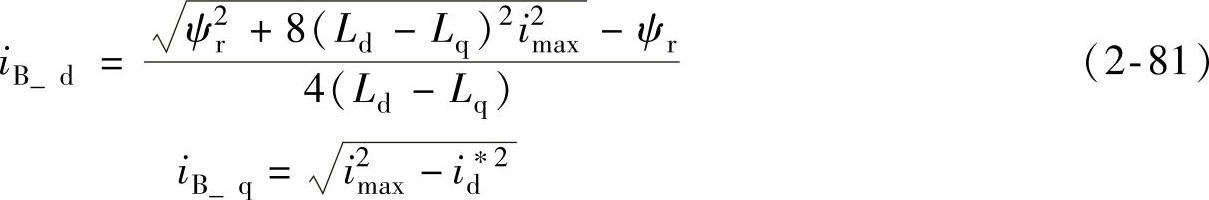
将式（2-81）代入式（2-63），得到B点角速度为(www.xing528.com)

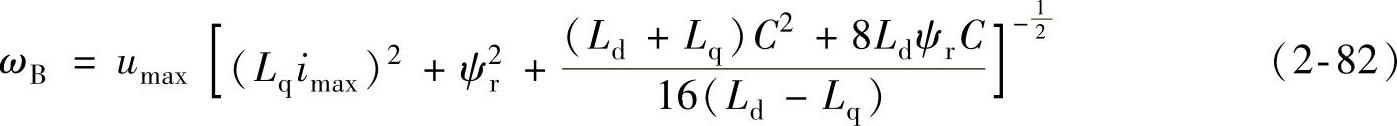
式中

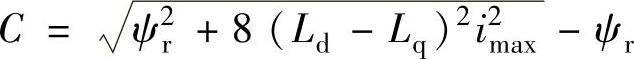
结合图2-16分析得到，B点（单位电流电磁转矩最大控制），比A点（i_d=0控制）在角速度和转矩上都有所提高，即

ω_B＞ω_A

T_B＞T_A （2-83）

当转速继续上升，在单位电流电磁转矩的最大控制下，电流矢量轨迹沿着最优控制曲线，由B向原点移动，达到原点时，转速和转矩值与i_d=0控制方法得到的一样。另外，当L_d=L_q时，则由式（2-76）、式（2-73）、式（2-80）和式（2-75）可得到

cosγ=0

i^∗_d=0

i^∗_q=i

T^∗_e=p_nψ_ri^∗_q

f（γ）=p_nψ_r （2-84）

由此可见，对隐极同步电动机来说，单位电流转矩的最大控制策略与i_d=0的控制策略完全一样。

3.弱磁控制

永磁同步电动机的弱磁控制思想类似于他励直流电动机的调磁控制。当他励直流电动机端电压达到最大电压时，只能通过降低电动机的励磁电流改变励磁磁通，在保证电压平衡的条件下，使电动机能用更高的转速进行恒功率运行。也就是说，他励直流电动机可以通过降低励磁电流达到弱磁增速的目的。对于永磁同步电动机而言，励磁因永磁体的产生而无法调节，只能通过调节定子电流，即增加定子直轴去磁电流来维持高速运行，以达到弱磁增速的目的。显然，电动机等效气隙越大，电枢反应去磁作用越小；反之，电枢反应去磁作用越大。因此，弱磁控制通常以凸极内置式永磁同步电动机居多，而面对插入式永磁同步电动机由于等效气隙较大，采用弱磁控制效果相对不明显。

图2-17画出了电流相平面上的电流极限曲线、电压极限曲线和最优控制曲线的关系。图中，当电动机转速等于或超过额定转速时，定子电压达到极限值，电压极限曲线在电流相平面上成为一簇椭圆，椭圆的中心点P为（-ψ_r/L_d，0），椭圆的长短半轴分别与电流相平面的坐标轴平行，长度分别为u_max/（ωL_d）和u_max/（ωL_q）。显然，额定转速时电流相平面上的电压极限曲线最大，即最大电压极限曲线。随着转速升高，椭圆长短半轴的长度与转速成反比，电流相平面上的电压极限曲线不断地朝椭圆中心点缩小。

转速增大时，需要增大直轴去磁电流，为了维持电流不超过极限值，在增大直轴电流的同时，应减小交轴电流。把式（2-64）代入式（2-63）得到角速度与直轴去磁电流关系：

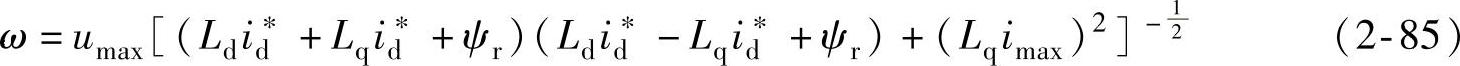
永磁同步电动机进行弱磁控制，转速以恒定电磁转矩上升到B点，从B点沿着电流极限曲线转速继续升高，电磁转矩将不断下降，最终交轴电流等于零，即电磁转矩也等于零，这时电压极限曲线与电流极限曲线相切于C点（-i_max，0）。故电动机能达到的最高理想空载角速度由式（2-63）或式（2-85）不难得到

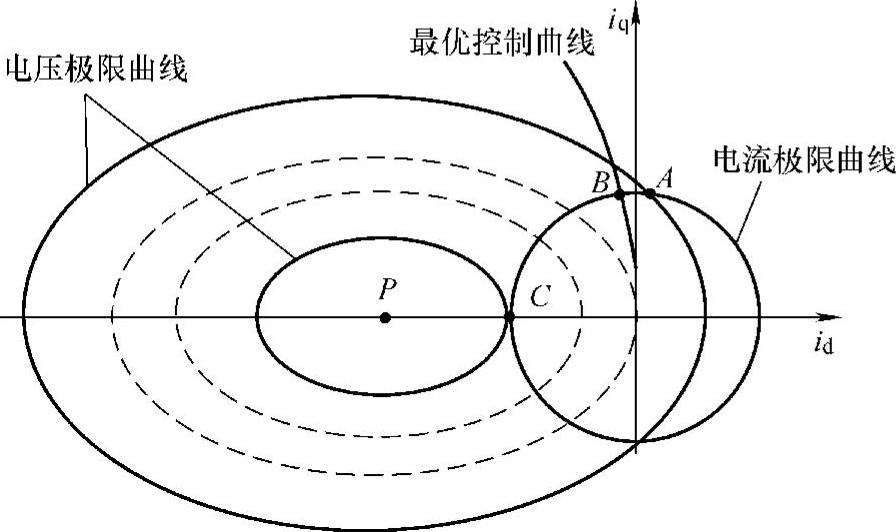
图2-17 定子电流矢量轨迹

图2-18的情况有所不同，由于电压极限曲线的椭圆中心点P（-ψ_r/L_d，0）在电流极限曲线内部，即ψ_r＜i_maxL_d。式（2-67）限制了定子电流直轴分量的增大，理论上，电动机在C点直轴电流分量最大为-ψ_r/L_d，实际应用中要避开退磁曲线的拐点。C点是转速上升中的一个转折点，由B到C的转速上升过程为弱磁控制[式（2-85）]，由C到P的转速上升过程会用到另外一种控制策略，称为恒功率控制，该控制保证电流直轴分量恒定为-ψ_r/L_d，通过控制电流交轴分量减小来实现升速的目的，这样电磁转矩将线性减小，而电磁功率保持不变。

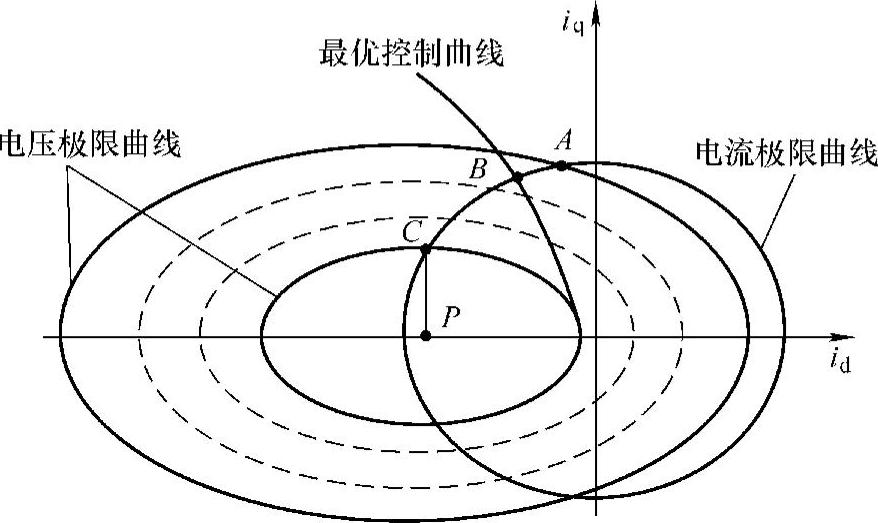
图2-18 弱磁控制电流轨迹

在转折点C的位置，电动机具有最大的直轴去磁电流，或者说转子永磁体完全达到去磁的状态，并且因为i_q不等于零，因而存在一定的电磁转矩。C点直轴最大去磁电流分量和对应的交轴电流分量分别为

由C到P轨迹的电磁转矩和转速分别由式（2-32）和式（2-85）简化得到

当接近P点，不难得到电动机最终交轴电流等于零，即电磁转矩也等于零，而使转速上升的范围大幅度扩大。

把式（2-89）和式（2-31）代入式（2-88）得到电磁功率为

由上式可知，在CP段轨迹控制策略保持电磁功率恒定，其值是定子电流最大直轴分量与电压极限值的乘积。

在C点转矩最大，它可由式（2-87）代入式（2-88）得到

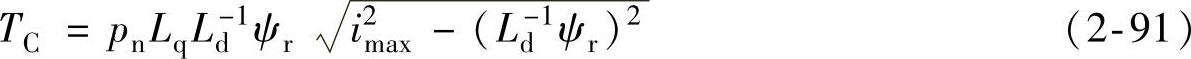
将式（2-87）代入式（2-89），得到C点角速度为

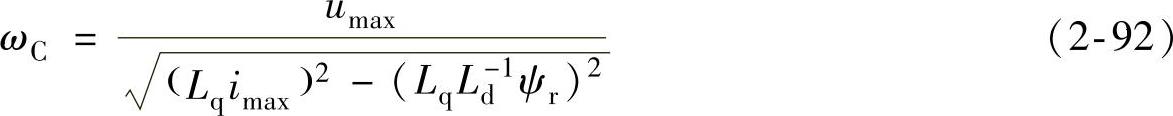
由上述分析可以看出，电压极限曲线的椭圆中心点位置直接影响电动机的最高运行转速和输出转矩。

4.不同控制策略的转速-转矩特性

永磁同步电动机控制过程中受到电流与电压极限曲线的约束，因此电动机设计时，就要根据永磁同步电动机的控制策略、电动机运行的最高转速和额定转速的要求，合理地设计电流极限曲线和最大电压极限曲线的相对位置，使得永磁同步电动机能够满足驱动系统的要求。永磁同步电动机宽范围调速的机械特性如图2-19所示，图中在额定转速以下，转矩与转速关系是水平线，电动机能以恒转矩驱动。额定状态工作点A是电流极限曲线与电压极限曲线和q轴的交点，其角速度为式（2-70）；机械特性上最大电磁转矩工作点B是电流极限曲线与电压极限曲线和最优控制曲线的交点，其角速度为式（2-82）；如果转子转速继续升高，那么定子电流将由B沿着电流极限曲线移动，当直轴电流达到最大去磁电流的工作点C时，如果电压极限曲线的椭圆中心在电流极限曲线外部，那么C点是最高转速下电压极限曲线与电流极限曲线的切点，机械特性很快下降，如图中BC’曲线所示；如果电压极限曲线的椭圆中心在电流极限曲线内部，那么电动机转速达到C点，其角速度为式（2-92），电磁转矩为式（2-91），以后转速继续升高，直轴电流维持最大去磁电流不变，电磁功率保持恒定，然而交轴电流逐渐减小，电磁转矩也相应地线性减小，当交轴电流等于0时达到P点，即电磁转矩等于0，转速达到最高。

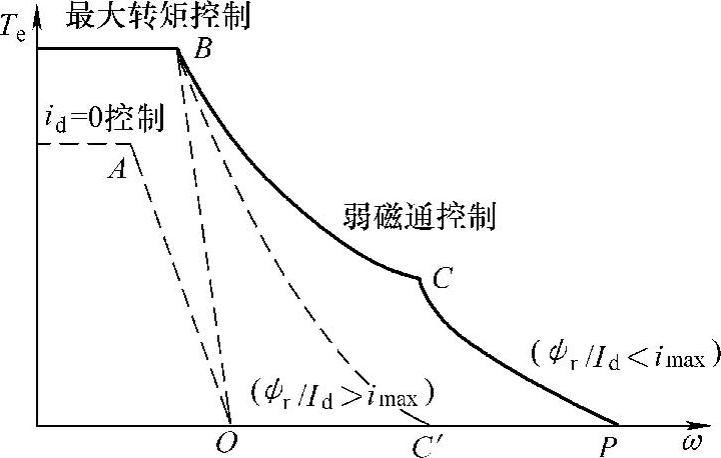
图2-19 不同控制策略的转速-转矩特性