如何减少电机纹波转矩？

为了产生恒定的电磁转矩，PMSM的反电动势和由逆变器输入的定子电流都必须是正弦波的。但实际上，由于永磁体形状上的原因和定子齿槽的存在，反电动势不可能是正弦波的。另外，由逆变器输入的定子电流，尽管经PWM控制器控制可以十分逼近正弦波，但它还会含有许多谐波，这样必然会引起转矩的波动。通常，将这种由反电动势或定子电流谐波而引起的转矩波动称为纹波转矩。

下面从谐波分析入手，来定量计算转矩纹波的大小。因为钕铁硼永磁材料的磁导率与空气的磁导率相近，为了充分利用磁铁，有时极弧系数选取过大，较难保证主极磁场在空间按正弦规律分布，使各相感应电动势中存在着3、5、7、11、13次等谐波。此外，驱动器电流也有谐波存在，主要谐波次数为5、7和11次等。按照式（2-40）计算，推导可得到

式中

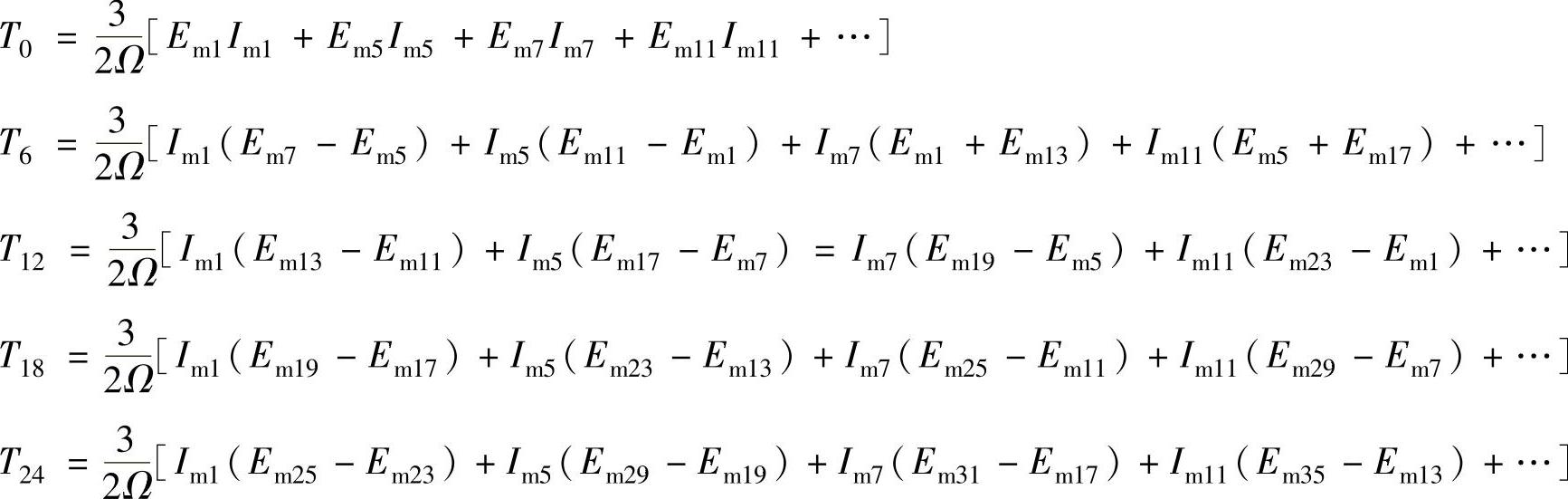
从式（2-55）可见，电磁转矩中含有频率为基波频率6倍的纹波转矩，纹波的脉动幅值与反电动势和电流偏离正弦的程度有关。图2-10绘出了在给定情况下产生的转矩纹波。可以看出，其主要成分是6次谐波转矩。通常，用纹波系数来定量地描述转矩脉动程度，它定义为

式中 T₀——平均转矩；

T_p——转矩纹波的峰值。(www.xing528.com)

如果已知各谐波转矩的幅值，则C_tr可表示为

式中T_H=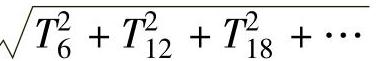

图2-10 转矩纹波（梯形波电动势和正弦波电流）

在高速区，这个纹波有可能被转子惯量滤掉。但在低速区，它将使转子速度发生波动，从而严重影响伺服驱动的性能，特别是会使位置伺服准确度和重复性变坏。因此，应尽量减小转矩纹波，尽量减小定子电流和反电动势中5、7、11和13次等较低次谐波的幅值，使转矩曲线越平滑越好。

反电动势中的谐波分量与永磁体励磁磁场的分布和定子绕组的构成有关，采用合适的短距比和分数槽绕组等方法都可有效地较小感应电动势中的低次谐波。电流中的谐波分量与PWM控制有关，目前消弱方法的研究成果较多，有的已经使用在电动机驱动系统中，取得了良好的效果，例如SVPWM，可使定子电流中不含低次谐波，而只含某些高次谐波分量，虽然这些高次谐波电流会使转矩产生高频振荡，但因幅值很小，频率很高，很容易被转子转动惯量阻尼掉。