D型五螺杆泵齿形曲线存在的问题详解

在O.А.Пыж著作中D型五螺杆泵的螺杆齿形曲线存在如下的问题：螺杆螺旋的传力齿形曲线的螺旋面在长幅外摆线de和渐开线ef两条曲线的连接处——即e点处出现拐点，不能光滑连接，形成一条凸棱。在理论上运行时似乎两根螺杆的螺旋面会在e₁点和e₂点啮合，实际上由于螺杆和上、下滑动轴承之间存在间隙，螺杆旋转时会有所晃动，以及加工误差等因素，因此运行时e₁点和e₂点会产生啮合错位，这样e₁点和e₂点形成的螺旋面上的两条凸棱就会造成运行的不平稳和噪声的增大，凸棱也容易被磨损，降低了泵的使用寿命，而且磨损的磨屑也增加了可能造成螺杆或滑动轴承等的损坏，影响泵的可靠性（图5-2）。

现只需证明齿形曲线在e点理论上是否存在着拐点，若在e点处相连的两段曲线的斜率相等，即它们的曲线方程式的一阶导数相等，就证明连接是光滑的；若不相等，则证明存在着拐点。

由式（4-126）可得de曲线在e点的斜率为

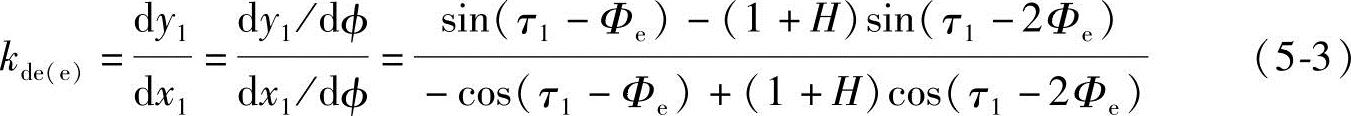
由式（4-71）可得

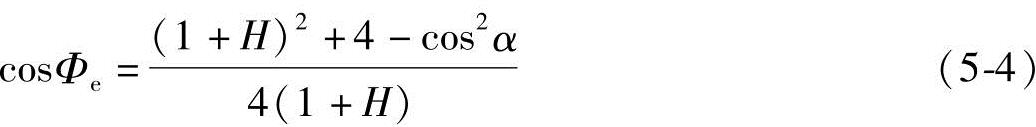
将表4-4中的α、H和τ₁值代入式（5-4）和式（5-3），可得

k_de（e）=4.96

由式（4-67）可得ef曲线在e点的斜率为(www.xing528.com)

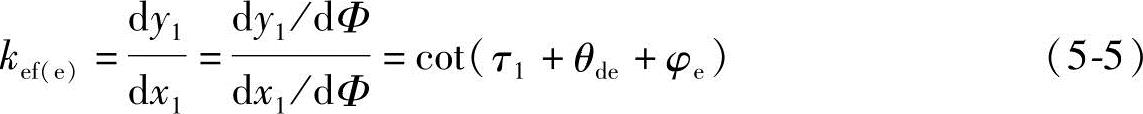
由式（1-46）和表4-4知：

将表4-4中的τ₁、式（5-6）和后面计算所得的列入表4-5中的θ_de代入式（5-5），可得

k_ef（e）=2.52

由此可见，k_ef（e）≠k_de（e），即两段曲线de和ef在e点相交不光滑，出现拐点。因此这样的型线相连接并不理想。

渐开线ef和短幅外摆线fg相连处的f点的情况，可用相同的方法证明，这两段曲线在f点处的斜率：

k_ef（f）=k_fg（f）=0.77

因此此处曲线的相交是光滑的，曲面在f点无凸棱。