螺杆啮合时螺旋面不干涉的条件

两根螺杆螺旋面的顶圆和根圆直径相同、螺旋为单头以及螺旋螺距固定不变的轴截面齿形为方牙形剖面的螺杆，当两根螺杆的螺旋相啮合时，螺旋面的两侧会形成两条间隙δ₃。为了判断这两条间隙，必须研究螺旋表面的相互位置。

图4-10为相互啮合的螺旋面投影在垂直于螺杆轴线的平面S上，形成有公共弦AB的两个弓形ACB和ADB。假设螺旋表面与S平面成α角，螺杆O₂的螺旋表面位于螺杆O₁的螺旋表面之上以及坐标轴的起点为平面S上的螺杆O₁的螺旋表面的K₁点。

在S平面上ADBCA范围内任取一点M，通过点M作垂直于S平面的垂线并与螺杆O₁和O₂的螺旋面相交。该垂线与螺杆O₁的半径为ρ₁的螺旋线K₁M₁相交，而对于螺杆O₂，该垂线与半径ρ₂的螺旋线K₂M₂相交。

螺杆O₁的垂线MM₁为

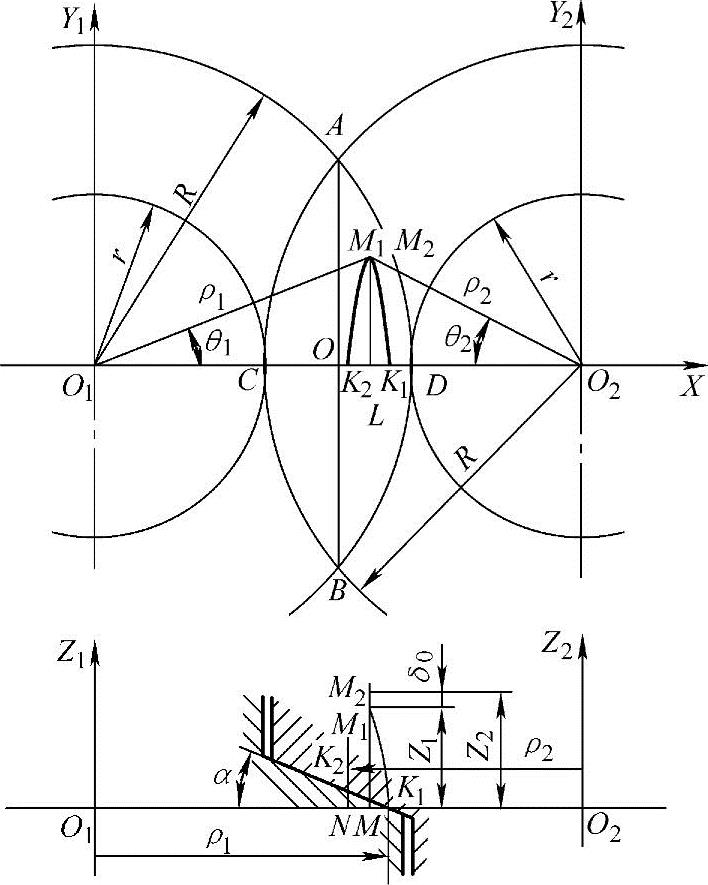
图4-10 间隙δ₃的确定

螺杆O₂的垂线MM₂为

式中 K₂N=（ρ+ρ₂-R-r）tanα；当θ₂=0时，K₂N即为平面S之上的K₂点的起始高度。

显然，点M₁和M₂之间的高度差就是两根螺杆的螺旋面之间的间隙δ₀，由式（4-52）和式（4-53）知，ADBCA范围内任意点M处的两根螺杆螺旋线之间的间隙δ₀为

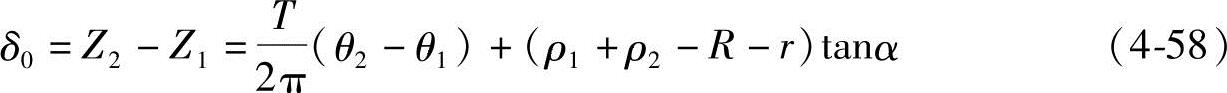
若螺旋轴截面上的剖面为矩形和正方形，即α=0时，则间隙δ₀为

(www.xing528.com)

在ADBCA范围内位于AB线上的点，由于ρ₁=ρ₂，故θ₂=θ₁，由式（4-59）可知此种情况下δ₀=0。

在AOD范围内的所有点，由于ρ₁＞ρ₂，故θ₂＞θ₁，所以δ₀为正值，即螺杆O₂的螺旋面位于螺杆O₁的螺旋面之上；在AOC范围内的所有点，有ρ₁＜ρ₂、θ₂＜θ₁，故δ₀为负值，即螺杆O₂的螺旋面位于螺杆O₁的螺旋面之下。也就是说在AOC区域，螺杆O₂的螺旋切入到螺杆O₁的螺旋面之中，即螺旋啮合时发生干涉！COB范围的情况也相似，该区域的δ₀＞0，而在BOD范围内则δ₀＜0，因此，在剖面α=0时螺旋面沿着线AB和CD相交。由上可知，在T不变时，不同的ρ值升角不同。ADBCA范围内不同点的间隙δ₀也不相同。在和弧上的点，间隙δ₀的绝对值最大，即θ₂-θ₁之差最大。

若螺旋轴截面上的剖面为α≠0的梯形或三角形，沿着AB线上的点θ₁=θ₂，则式（4-58）变为

δ₀=（ρ₁+ρ₂-R-r）tanα （4-60）

由式（4-56）可知，在A点和B点ρ₁=ρ₂=R的情况下，δ₀=（R-r）tanα；而在CD直线上的点，由于ρ₁+ρ₂=R+r，故δ₀=0。显然，AB和CD两直线的交点O处为δ₀=0，发生螺旋面相交。由式（4-54）知，沿着相交线上的所有点（即δ₀=0），都应遵循下列等式

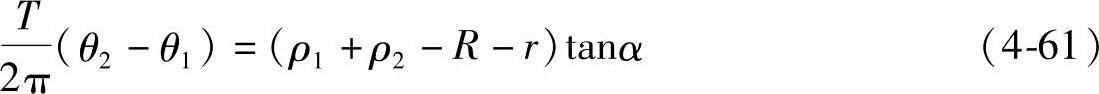
由上面分析可知，一对螺杆的螺旋相啮合时，能够正常运行的条件，必须使ADBCA范围内的螺旋表面不相交，即两根螺杆的螺旋表面互不干涉：一根螺杆的螺旋不切入另一根螺杆的螺旋之内。为此必须求得一根螺旋切入另一根螺杆螺旋的最大值，这个值就是螺旋面为避免相交所必需移动的值，称之为理论上必需的间隙值δ_l，也就是理论上两根螺杆的螺旋面之间必需保持的最小间隙值。在这种情况下表面相交处的间隙δ₃就等于δ_l，若间隙值小于这个δ_l值，就必然会发生干涉，无法正常运行。

在此不详细推导δ_l的解法，仅给出Н.Г.женовак提供的计算结果，列在表4-1中。

表4-1 理论上必需的间隙值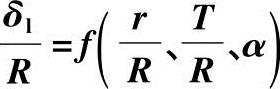

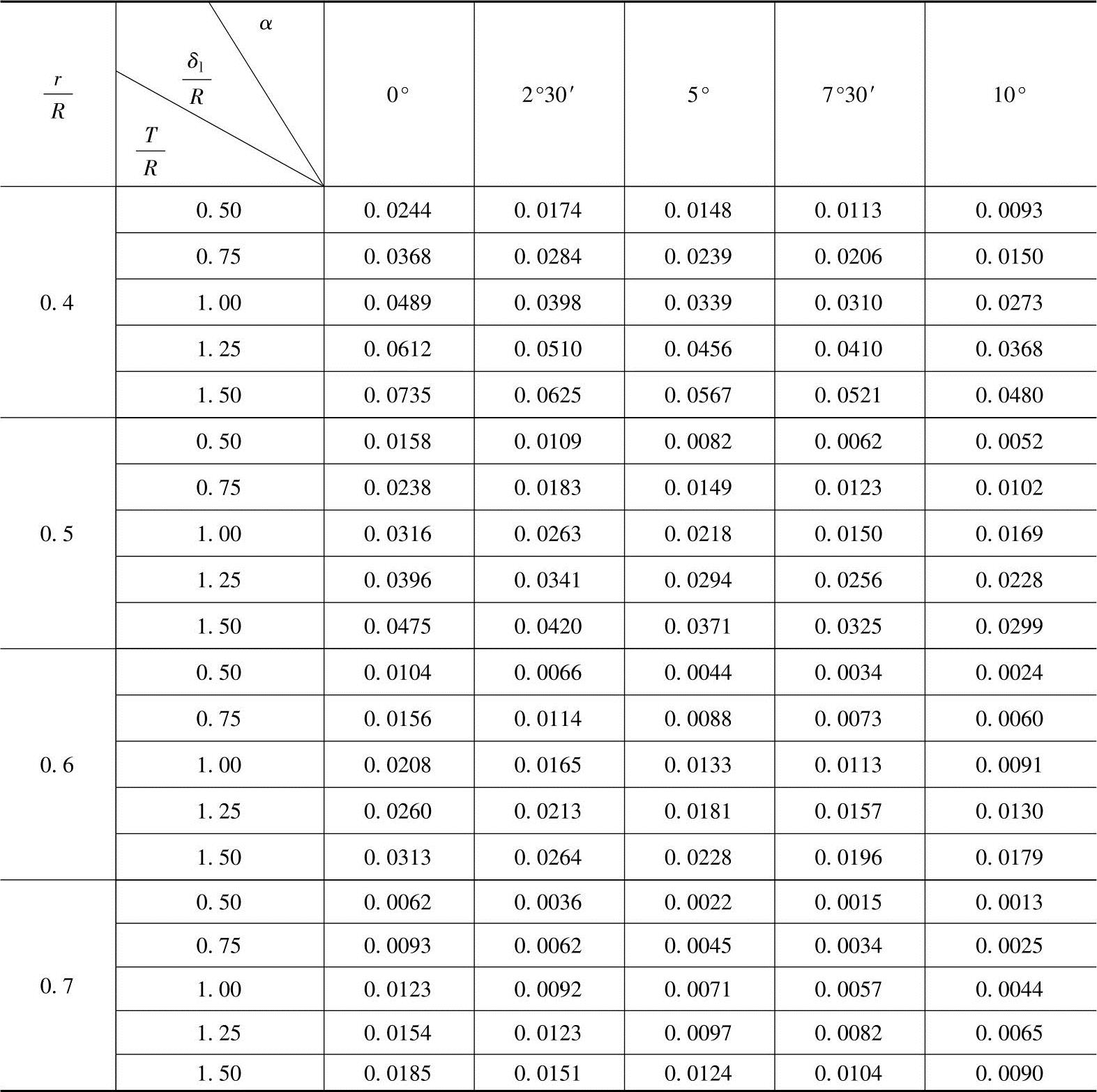
当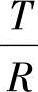增大时，δ_l增大；当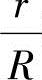减小时，δ_l增大；当α减小时δ_l也增大。

解决两根螺杆的螺旋啮合时出现干涉现象的办法是用减小螺旋厚度，即减小螺旋顶圆宽度的方法来实现。

故螺旋表面之间任意点的间隙 δ₃=δ₀+δ_l （4-62）