螺杆螺旋端面的齿形曲线一侧为密封齿形abc,另一侧为传力齿形def(图4-14)。
(1)密封齿形曲线abc 密封齿形曲线由长幅外摆线ab和bc组成。
1)长幅外摆线abab曲线为螺杆端面以一根螺杆螺旋的节圆为动圆,沿着定圆为另一根螺杆螺旋的节圆作纯滚动时,动圆上齿顶圆的b′点为摆点的轨迹。
若坐标系的Y轴通过螺旋槽中心,即Y轴转θ0=τ1角(图4-14),则由式(1-38)可知,ab曲线的方程式为
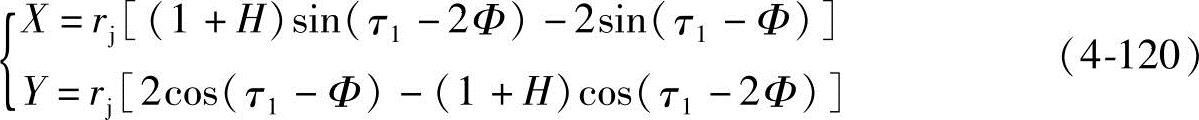
式中 H——齿顶高系数,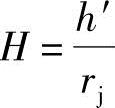 ,其中h′为齿顶高度,h′=h1′=h2′。
,其中h′为齿顶高度,h′=h1′=h2′。
ab曲线任意点的齿形转角Φi为
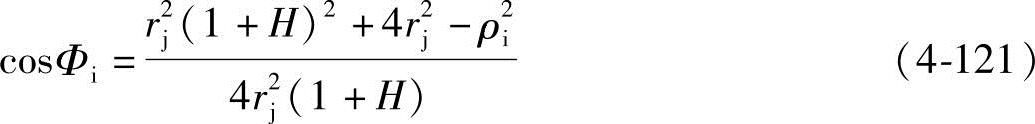
式中 ρi——ab曲线任意点的的动径;对于b点,ρb=rj(1+Hx),其中Hx为斜棱起始点高度系数,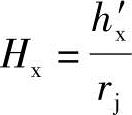 ,hx′为斜棱起始点高度,即斜棱起始点b至节圆距离。
,hx′为斜棱起始点高度,即斜棱起始点b至节圆距离。
ab曲线的极角θab为
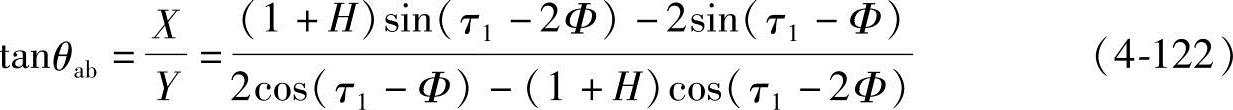
2)长幅外摆线bc。bc曲线为螺旋端面以一根螺杆螺旋的节圆作动圆,沿着定圆为另一根螺杆螺旋的节圆作纯滚动时,动圆上半径为rx=rj(1+Hx)的斜棱起始点b′为摆点的轨迹。
若坐标系y轴通过螺旋槽中心,则由式(1-38)可知,bc曲线的方程式为
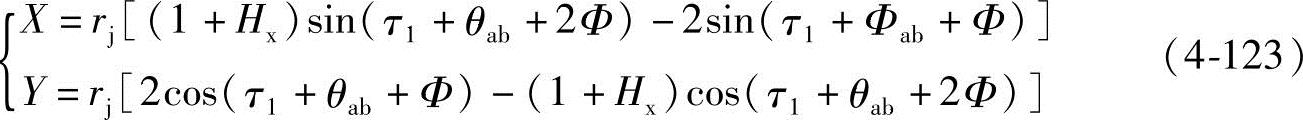
bc曲线任意点的齿形转角Φi为
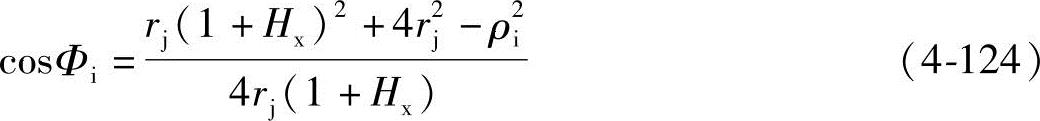
式中 ρi——bc曲线上任意点的动径;对于C点,ρc=rj(1+H)。(https://www.xing528.com)
bc曲线的极角θbc为
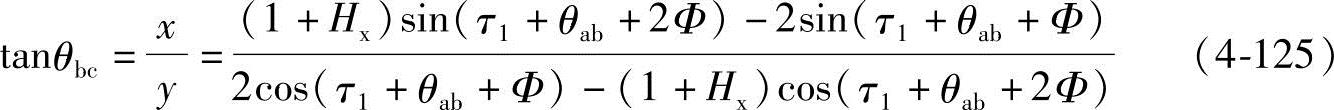
(2)传力齿形曲线def 在О.А.Пыж的著作中,B型双螺杆泵螺杆螺旋的传力齿形曲线仅为一条图4-14中的渐开线d′f。笔者认为,若传力齿形曲线仅仅为一条渐开线,则其啮合线必不能通过两根螺杆螺旋的齿顶圆和齿根圆的切点,这样的啮合线就不连续(详见后面啮合线分析),因此不能满足第一类密封性的要求,这样的齿形自然不能使密封腔将吸入腔和排出腔有效地隔开,因此也就不能把B型双螺杆泵列入密封型螺杆泵的范畴。而B型双螺杆泵主要用于高压工况,其密封腔的密封性尤为重要,它直接影响到泵的容积效率。因此,笔者以为要想尽可能地使螺旋齿形的啮合线连续,实现满足第一类密封性的基本要求,就应对传力齿形曲线d′f进行修正。笔者提出渐开线d′f和齿根圆之间需存在一段长幅外摆线de,在e点处为该长幅外摆线和渐开线d′f的交点,这样传力齿形曲线就由de和ef两条曲线组成(图4-14),这样的齿形在后面的分析中,会证明是能使密封腔将吸入腔和排出腔有效地隔开,B型双螺杆泵在高压工况下也能得到更高的容积效率,也才是真正的密封型螺杆泵。
1)长幅外摆线de。de曲线为螺杆螺旋端面以一根螺杆的节圆为动圆,沿着定圆为另一根螺杆螺旋的节圆作纯滚动时,动圆上螺旋顶圆的f′点为摆点的轨迹。
由图4-14可知,de曲线和ab曲线虽都是长幅外摆线,但在坐标系中的位置不同,故它们方程式中某些项的符号就需作相应的变动。若坐标系Y轴通过螺旋槽中心,则de曲线的方程式为
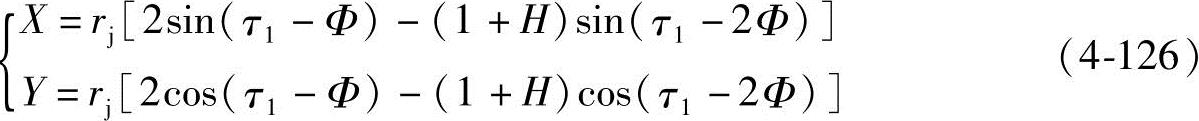
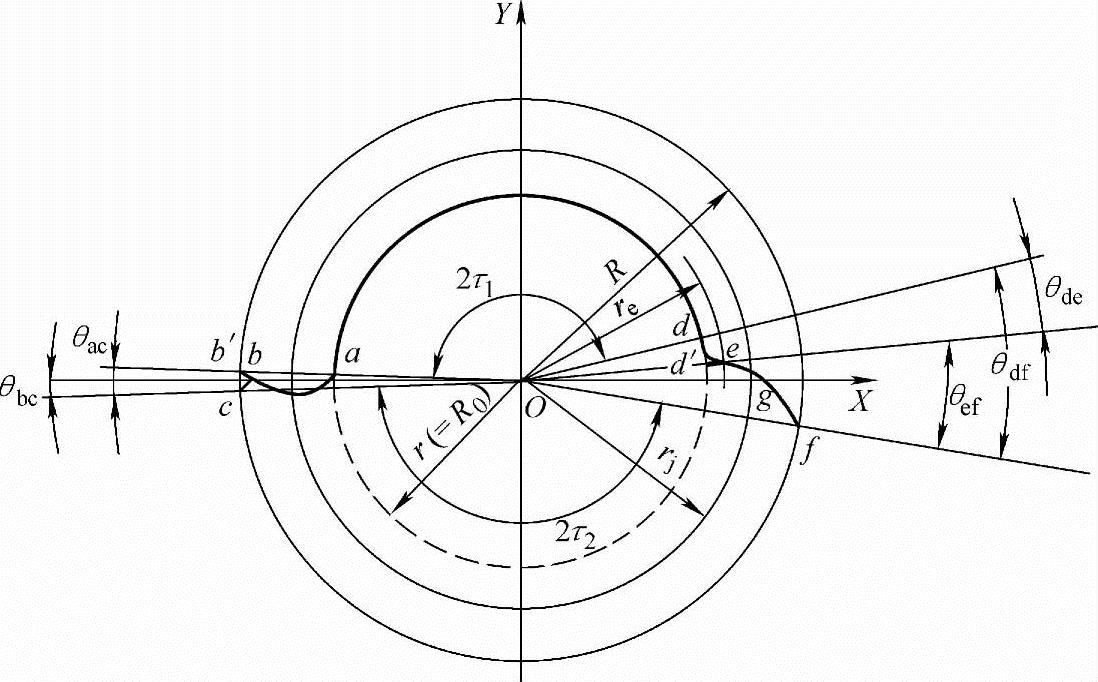
图4-14 B型双螺杆泵螺杆螺旋齿形曲线
de曲线任意点的齿形转角Φi为
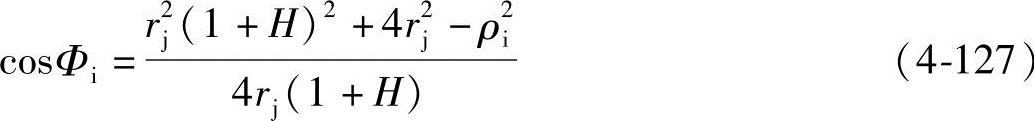
式中 ρi——de曲线上任意点的动径;对于e点,由后面式(4-134)计算得ρe=0.856373rj。
de曲线的极角θde为
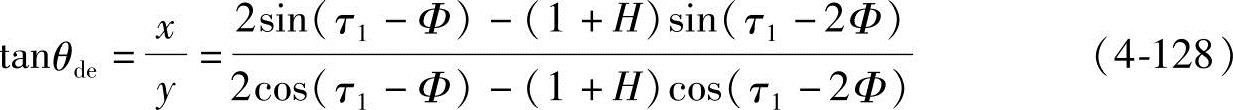
2)渐开线ef。渐开线ef是以螺旋齿根圆为基圆(即基圆半径r0=r),由基圆上的一点展开形成的。渐开线d′f与长幅外摆线de相交于点e,从e点到渐开线与齿顶圆的交点f之间的渐开线段,即为渐开线ef。
若坐标系的Y轴通过螺旋槽中心,由式(1-50)可得ef曲线的方程式为
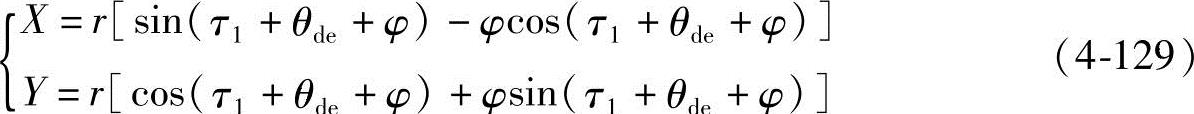
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




