螺旋螺杆齿形曲线分析

（1）螺杆螺旋面的型线组成 主动螺杆和从动螺杆螺旋面的齿形曲线相同，螺旋面两侧的形状对称，螺旋头数相同，螺旋导程的尺寸固定不变，型线如图4-2所示：ab曲线为长幅外摆线，bc曲线为外摆线，故螺旋面型线为摆线组合而成的abc曲线。

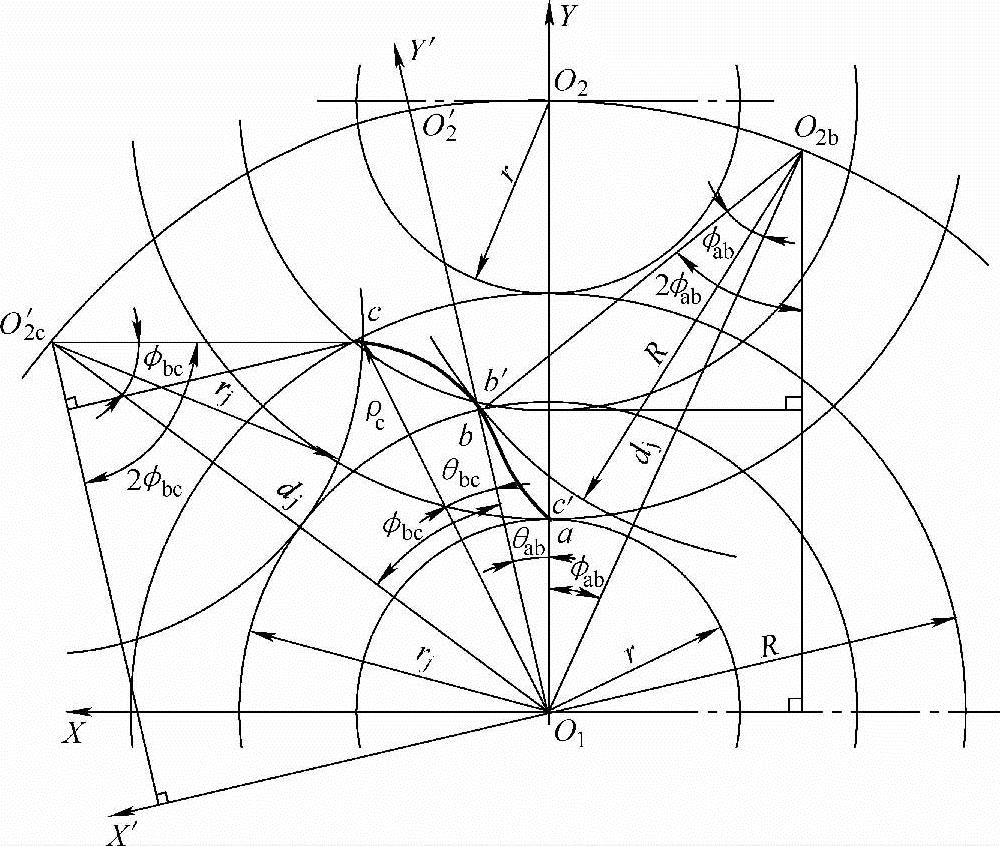
图4-2 螺杆螺旋的齿形曲线

1）长幅外摆线ab。以螺杆螺旋端面上的节圆O₁作定圆，另一螺杆螺旋的节圆O₂为动圆，当动圆沿着定圆作顺时针纯滚动时，动圆外以O₂为圆心的螺旋齿顶圆上的C′点为摆点的轨迹，即为长幅外摆线ab。

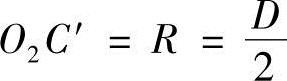
2）外摆线bc。以螺杆螺旋端面上的节圆O₁作定圆，另一螺杆螺旋的节圆O₂′为动圆，当动圆沿着定圆作逆时针纯滚动时，动圆O₂′节圆上的b′点为摆点的轨迹，即为外摆线bc。

O₂′b=r_j

（2）齿形曲线方程式

1）长幅外摆线ab方程式。O₁a=r，O₁b=r_j和O′_2bb=R，由式（1-17）得方程式为

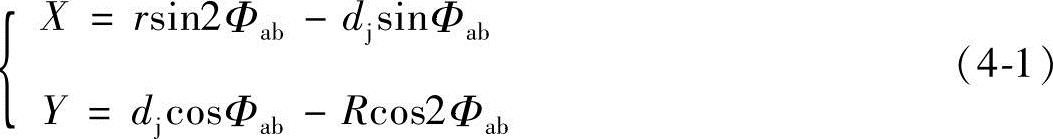
式中 Φ_ab——齿形曲线ab的齿形转角，即型线起始位置a随着动圆滚至终点位置b，此时两圆心连线O₁O₂和O₁O_2b之间的夹角为Φ_ab。

所以

式中 ρ_b——动圆O₂滚动时，动圆外c′点的轨迹与定圆O₁的节圆的交点b在O₁圆上的半径

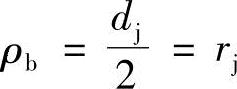
ab曲线上任意点i的齿形转角Φ_i为

式中 ρ_i——齿形曲线ab上任意点i的动径，即r→r_j中任意点i在O₁圆上的半径。

2）外摆线bc方程式。O₁b=r_j，O₁c=R和O_2c′C=r_j，在y′轴通过b点的坐标系X′O₁′y′中，由式（1-10）得方程式为

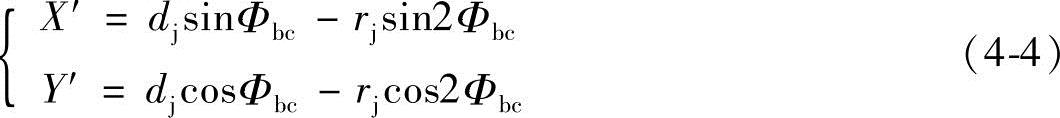
式中 Φ_bc——齿形曲线bc的齿形转角，即型线起始位置b′随着动圆滚动至终点位置c，此时两圆心连线O₁O₂′和O₁O_2c′之间的夹角为Φ_bc。

式中 ρ_c——动圆O₂′滚动时，动圆b′点的轨迹与定圆O₁的齿顶圆的交点c在O₁圆上的半径，

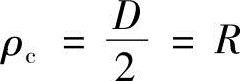
bc曲线上任意点i的齿形转角Φ_i为(www.xing528.com)

式中 ρ_i——齿形曲线bc上任意点i的动径，即r_j→R中任意点i在O₁圆上的半径。

若Y′轴旋转θ_ab角，将X′O′₁y′坐标系中bc曲线的坐标X′、Y′式（4-4）转换到XO₁Y坐标系，则齿形曲线bc的坐标方程式式（4-4）变为

（3）齿形曲线极角

1）长幅外摆线ab的极角θ_ab：

由式（1-18）可知，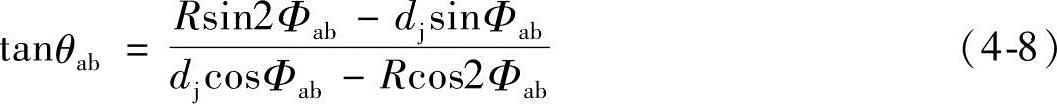

ab曲线上任意点i的齿形曲线极角θ_i为

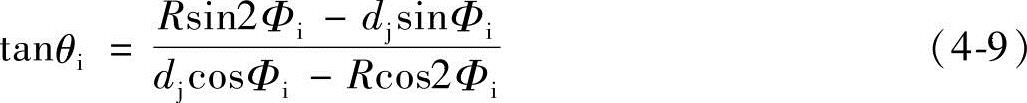
2）外摆线bc的极角θ_bc：

由式（1-11）可知，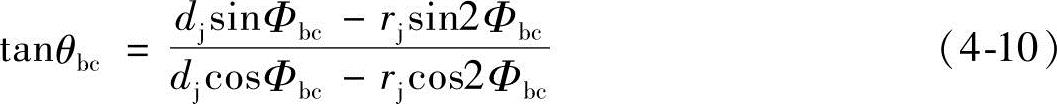

bc曲线上任意点i的齿形曲线极角θ_i为

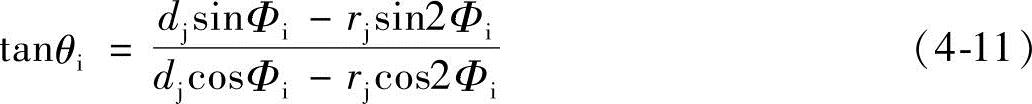
3）型线abc的极角θ_ac：

由式（4-8）和式（4-10）得到θ_ab和θ_bc，

可得θ_ac=θ_ab+θ_bc （4-12）

4）半径r处的齿根圆中心角2τ_r：

单头螺旋时2τ_r=（360°-2θ_ac）÷2 （4-13）

双头螺旋时2τ_r=（180°-2θ_ac）÷2 （4-14）

5）半径R处的齿顶圆中心角2τ_R：

2τ_R=2τ_r （4-15）

（4）螺杆轴截面的齿形曲线坐标方程式 在以螺杆轴线为Z轴的OρZ坐标系中