螺杆轴向压力的平衡与计算方法

（1）螺杆轴向压力 螺杆的轴向压力只考虑由介质静压力产生的轴向压力，介质动压力的影响很小，可忽略不计。

介质作用在螺杆的圆柱表面是不产生轴向压力的，故介质作用在螺杆上的轴向压力为作用在螺杆端面的轴向压力和作用于螺杆螺旋型面上的轴向压力之和，力的方向由排出腔指向吸入腔。

假设螺杆的端面完全处在排出腔和吸入腔的压力作用之下，由式（3-60）和式（3-83）可得

由式（3-49）和式（3-87）可得，作用在主动螺杆上的总轴向压力p_z1为

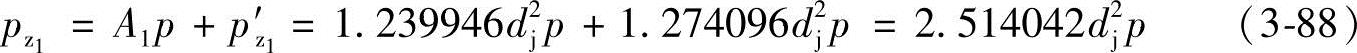
实际上，作用在主动螺杆上的轴向压力要大于式（3-88）的值，因为主动螺杆从原动机得到的力矩除了介质静压力对螺杆产生的力矩外，还需克服各种摩擦损失的那部分力矩。

由式（3-59）和式（3-83）可得，作用于一根从动螺杆上的总轴向压力p_z2为

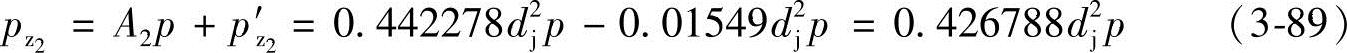
考虑到我国相当多的制造厂的采用2τ=0.18π的齿形中心角，故在此仍提供2τ=0.18π的有关值：A₁=1.267904d²_j，和A₂=0.428317d²_j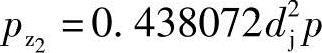，。由式（3-88）和式（3-89）得三根啮合在一起的螺杆总轴向压力应为

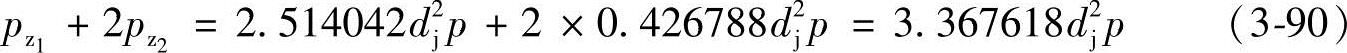
三根螺杆啮合在一起的总轴向压力也等于螺杆衬套横截面的过流断面面积A₃乘以全压力p，由式（3-32）知A₃p=3.367618d²_jp和式（3-90）相同，这也证明了上面的计算是正确的。

实际上螺杆采用平衡轴向压力的方法不同，螺杆实际承受的轴向压力就不是式（3-88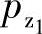）和式（3-89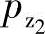）的值。轴向压力的平衡方法将在下面叙述。

某些学者和国外的制造厂在计算螺杆轴向压力时，还考虑泵在零压点工况摩擦损失引起的那部分力矩ΔM₀，ΔM₀的推导与式（3-70）相同，故产生ΔM₀的轴向压力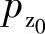为

式中 ΔP₀——泵在零压点工况时摩擦损失的功率。

所谓的零压点工况理论上应是泵进口压力和排出压力均为零时的工况。考虑到试验台的实际情况，我国标准规定：泵进口压力为-0.05～0.03MPa和出口压不大于0.05MPa时泵所运行的工况作为零压点工况。

日本川崎提出摩擦损失压力Δp的经验公式：

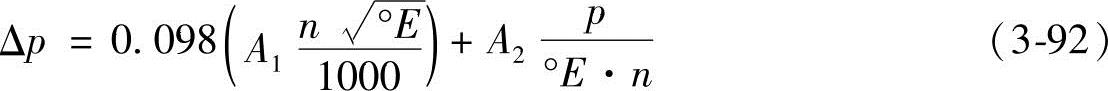
式中 °E——恩氏粘度。

显然，Δp对于不同性能参数和不同结构的产品，其值是不同的，故经验公式也不同。式（3-92）只适用于川崎公司的有关产品。当p=0MPa时，上述经验公式中的Δp即为零压点工况时摩擦损失压力Δp₀。

式中 系数A₁和A₂见表3-1。

表3-1 与摩擦损失压力有关的系数A₁和A₂的值

川崎B₄和B₆系列（均为高压泵）的Δp经验公式和式（3-92）有所不同。

B₄系列（排出压力为13.7MPa和20.6MPa）的，Δp单位为MPa；(www.xing528.com)

B₆系列（排出压力为24.5MPa）的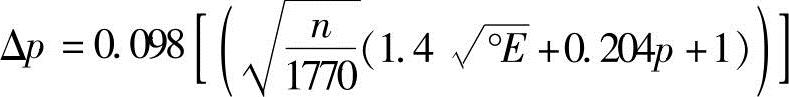，Δp单位为MPa。

将Δp₀代入而零压点工况时摩擦损失的功率公式ΔP_l=Δp₀Q_l代入式（3-91），即可求得。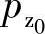

德国Leistritz公司等的样本中也针对他们的产品提出了摩擦损失Δp的经验公式，在此不再引述。

А.Е.Жмудь的著作中螺杆的轴向压力是不考虑零压点工况摩擦损失引起的因素，我国很多单位的设计也不计算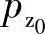，因为没有相应的经验公式，其数值相对较小，就略去不计，尤其对排出压力较高及机械效率较高的泵来说更是如此。

（2）螺杆轴向压力的平衡 泵的结构对介质作用于螺杆轴向压力的大小和方向有很大的影响，如：双吸式结构的泵能使介质作用于螺杆上的轴向压力基本平衡；又如立式结构的泵，螺杆的轴向压力还需考虑螺杆的质量。通常单吸式的泵，排出压力约为0.4MPa左右的低压泵，由于作用在螺杆上的轴向压力较小，可不必采取平衡轴向压力的措施，直接由推力块（图3-8中6）等方式承受，其余均设计卸荷结构。轴向压力的平衡有以下两种方式：

1）高压平衡。图3-8为典型的高压平衡螺杆轴向力的结构示意图。其特点是将排出腔的高压介质通过螺杆衬套2的孔（或在螺杆中钻孔）引入螺杆的底部来平衡轴向压力。这种平衡轴向压力方法的缺点是：由于排出腔和螺杆底部均为高压，使螺杆处于受压的状态，尤其对于高压小流量的泵，细长的从动螺杆刚度差，很容易因受压而弯曲。因此螺杆螺旋的外圆柱面和螺杆衬套孔之间的间隙，必须大于螺杆的弯曲变形。这个间隙太大，容积效率就会降低，间隙太小，螺杆就可能与螺杆衬套孔发生摩擦，容易发生“抱轴”。

通常高压平衡结构的轴向力计算如下：

假设主动螺杆的上平衡活塞直径d₁，主动螺杆的下平衡活塞直径为d₂，从动螺杆的下平衡活塞直径为d₃，作用于直径d₁的传动端的压力为一个大气压p_a（实际上仅仅是作用于主动螺杆伸出泵上盖端的直径d₄的端面为一个大气压，作用于d₁和d₄之间的为机械密封腔内的压力）（图3-8）。由式（3-88）知，主动螺杆的轴向压力p_z1可近似地看作

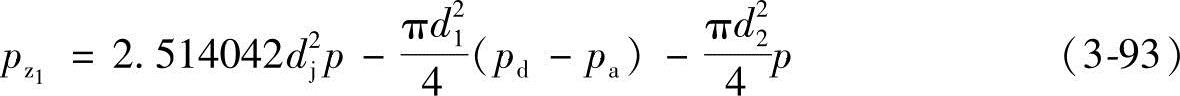
若吸入腔压力p_s和一个大气压力之差忽略不计，则式（3-95）可简化为

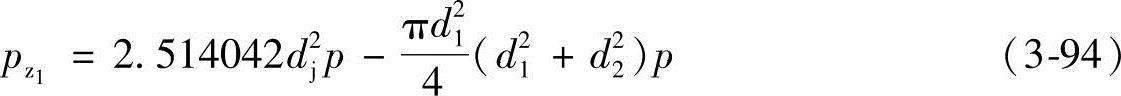
由式（3-91）知，从动螺杆的轴向压力p_z2为

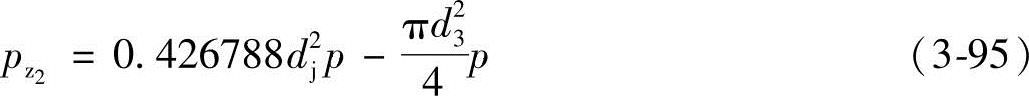
若考虑p_z0则计算时应加在p_z1之中。立式泵还需加上螺杆自重。

通常主动螺杆液力平衡后的剩余轴向力由滚动轴承承受（图3-8）；从动螺杆则在下平衡活塞的下端放置的推力块来承受剩余轴向压力。推力块应设计有储存介质的径向槽或径向斜面，使螺杆下端面与推力块在运转时有介质润滑。推力块承受剩余轴向压力的面积应是实际与螺杆下端面相接触的那部分面积。设计时需注意推力块上斜面的倾斜方向和螺杆旋转方向的关系。

2）低压平衡。图3-23所示为低压平衡的结构示意图。与高压平衡最主要的差别在于将图3-8中从动螺杆的下平衡活塞及从动螺杆的衬套7的位置由吸入腔一端改变到排出腔一端。这样从动螺杆受到排出腔中高压的作用时，螺杆处于伸长变形的状态。这种受力状态显然比高压平衡时从动螺杆处于受压缩状态要好。因为细长杆的从动螺杆不会产生弯曲变形引起的挠度，螺杆的螺旋外圆柱表面与螺杆衬套孔之间的间隙就可取得较小。正是这一特点，国外有些公司设计的高压三螺杆泵，索性就把螺杆衬套孔当作螺杆的滑动轴承用，这一改进使高压三螺杆泵的容积效率有了相当大的提高。

然而，上述的低压平衡从图3-23可看出也存在一个明显的缺点，因为从动螺杆的衬套是易损件，它位于排出腔一端，磨损后更换零件时，必须将整台泵全部拆开才行，这给用户使用时带来不便。而高压平衡只须将泵的下盖卸去即可更换从动螺杆的衬套和推力块，维修非常方便（图3-8）。

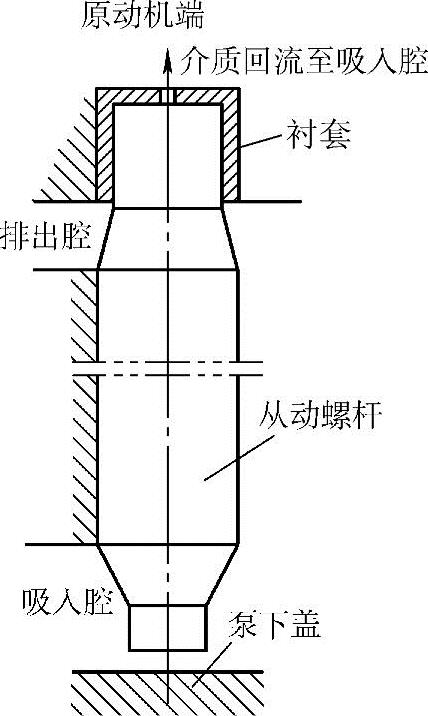
图3-23 螺杆轴向压力的低压平衡结构示意图

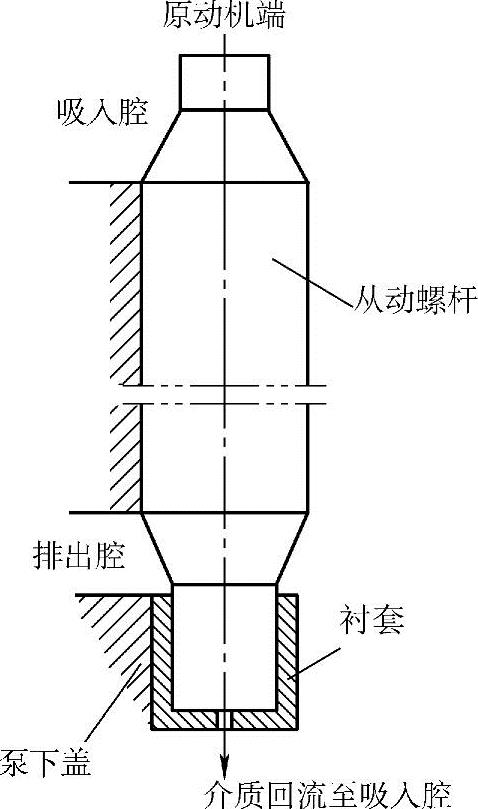
图3-24 结构改变后的螺杆轴向力低压平衡示意图

根据这两种液力平衡结构的优缺点，笔者在设计高压三螺杆泵时采用了低压平衡的方法（图3-24），但依然把从动螺杆衬套和推力块安置在泵的下盖处，只是把泵的排出腔和吸入腔位置对调，即将吸入腔设计在泵的传动端，而排出腔设计在近泵的下盖处。这样，螺杆受力后依然处在拉伸状态，易损件推力块和从动螺杆的衬套更换时仍只需卸下下盖即可（图3-8）。这样的结构保留了高压平衡和低压平衡结构两者的优点。实践证明这种结构是可靠的，设计时只需考虑机械密封腔内不一定是处于压力状态，而可能是处于吸入腔的真空状态这一变化。

低压平衡的轴向压力计算，对于从动螺杆，其轴向压力平衡的计算与高压平衡相同，可用式（3-95）；对于主动螺杆，若吸入腔内压力和一个大气压的差别忽略不计，则其轴向压力平衡的计算可近似地为