可降低从动螺杆力矩的介质作用优化方案

在讨论介质作用在螺杆上的力矩时，只考虑介质的静压力，介质动压力的作用忽略不计。

三螺杆泵运行时，泵的有效功都是主动螺杆产生，从动螺杆并不承受来自原动机的主动螺杆的力矩，仅仅起着“密封器”的作用。从动螺杆能否“卸掉”来自主动螺杆的力矩是与选取的齿形中心角2τ有关。

（1）介质作用在螺旋型面上的轴向力和作用于螺杆上的力矩的关系 三螺杆泵在不考虑泵内摩擦损失的情况下，螺杆从原动机得到的力矩等于介质静压力对螺杆产生的反作用力矩。由图3-20可知，介质静压力对螺旋的端面、螺旋齿形的顶圆和根圆的圆柱表面是不会对螺杆产生任何力矩的，因为静压力和螺旋的端面相垂直，和螺杆螺旋的圆柱表面平行。因此，只有作用在螺旋型面的静压力才会产生力矩。

在螺杆的螺旋型面上取无限小的面积dA，压力p作用在dA上的力为：dp=pdA，dp的方向为dA的法线方向。作用在dA上的力dp可分解成三个互相垂直的分力：轴向力dp_z、径向力dp_r和切向力dp_q。这三个分力可以表示为每一个分力等于压力p和面积dA在垂直于该力方向投影的积，即

由于轴向力dp_z和径向力dp_r均不能产生作用于螺旋型面上的力矩，只有切向力才会产生力矩，即

dM=rdp_q=rpdA_q （3-67）

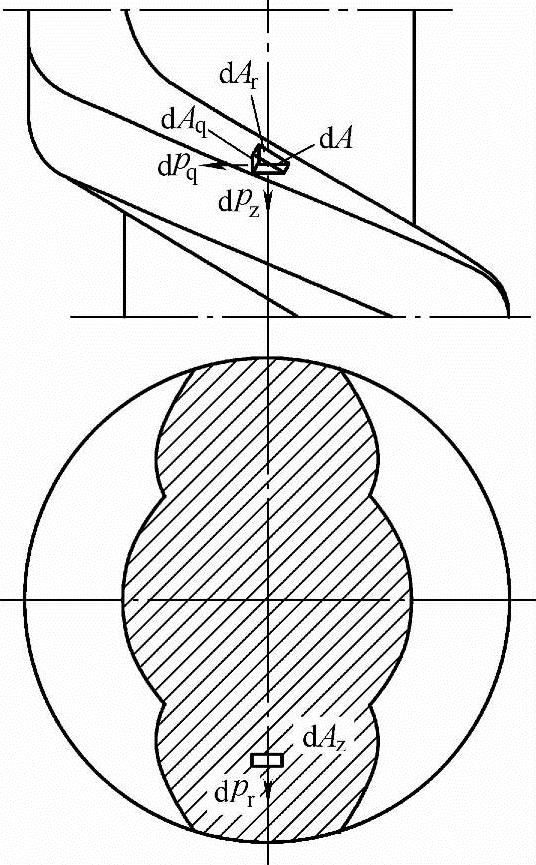
图3-20 介质静压力对螺杆螺旋面的作用

式中 r——无限小面积dA至螺杆中心线的距离，即dA的半径。

已知dA的投影dA_q和dA_z之比等于dA的半径r处螺旋线升角的正切，即

由式（3-66）、式（3-67）和式（3-68）得

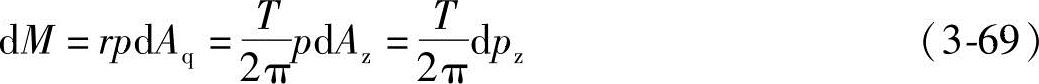
沿全部螺旋型面对式（3-69）积分，可得

式（3-70）表示作用于螺旋型面方向指向吸入腔的轴向力p_z转换成作用于螺杆上的力矩。

研究介质作用在从动螺杆上的力矩是很重要的，因为螺杆对介质作用的力矩应等于介质对螺杆的反作用力矩。如果从动螺杆依靠主动螺杆的传动而旋转的话，那么，这个传动力矩自然与介质对从动螺杆的反作力矩成正比。主动螺杆和从动螺杆之间的作用力越大，螺杆螺旋型面也就磨损越快。因此，希望作用在从动螺杆上的这一反力矩越小越好，当这个力矩是负值时，从动螺杆就不需要主动螺杆来传动，而是由这个负的力矩——即由介质作用产生的自转力矩来克服阻力自动旋转。这种情况下，从动螺杆就不起把机械能转化为介质压力能的作用，而只起“密封器”的作用，这是最为理想的情况。也是设计三螺杆泵时应追求的目标。

（2）齿形中心角2τ的大小与从动螺杆产生自转力矩的关系 若扭矩M作用在螺旋型面上的轴向力p_z指向吸入腔方向，则假设产生对原动机的力矩起相反作用的力矩为正；若作用在螺旋型面的轴向力指向排出腔方向，该力矩与原动机的力矩作用方向一致，则此种情况的力矩定为负。

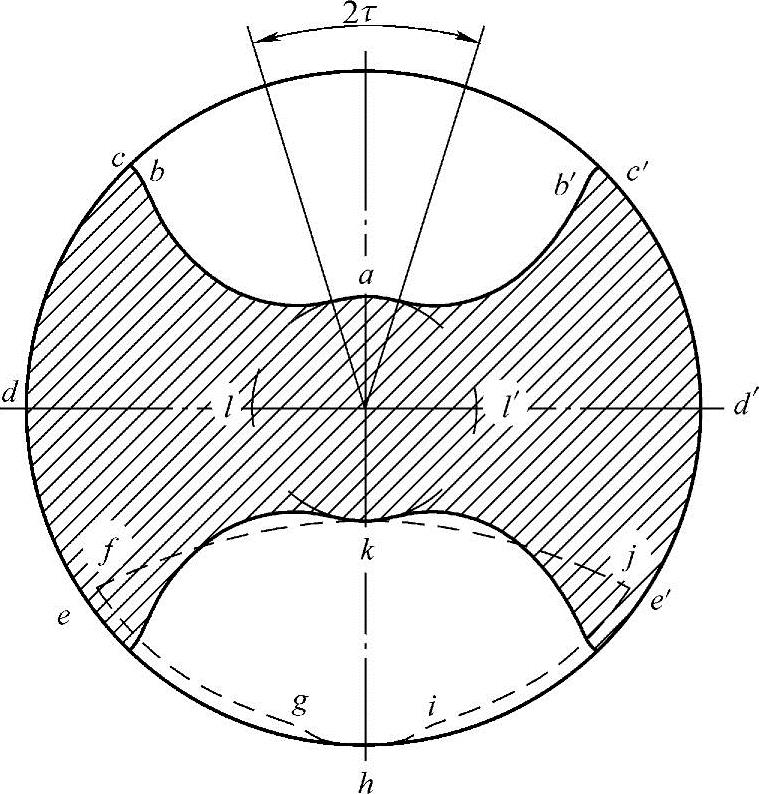
图3-21 修正后的从动螺杆齿形横截面（---为啮合线）

分析图3-21所示的修正后的右旋从动螺杆齿形，作用在一条螺旋槽上的轴向力等于作用在上螺旋型面和下螺旋型面的轴向力之差。

对于处于排出腔一端的一条螺旋槽，轴向力作用于螺旋槽下部螺旋型面的面积，由于主动螺杆的啮合复盖了螺旋槽螺旋型面的部分面积，故投影在从动螺杆螺旋齿形横截面上为作用在abcc′d′e′jkl′a区域上的轴向力，方向指向吸入腔，轴向力作用在螺旋槽上部螺旋型面的面积则投影在齿形横截面上ab′c′d′e′jihgfkl′a区域上的轴向力，方向指向排出腔。因此，作用在这条螺旋槽的总轴向力等于这两部分面积之差乘以p_d，即过流断面的面积abcc′b′a和螺旋啮合线包围的面积fghijkf之差乘以排出压力p_d。对处于吸入腔一端的一条螺旋槽情况相似，轴向力等于作用在这条螺旋槽型面投影在横截面上的面积abcc′b′a和fghijkf两部分面积之差乘以p_s。而封闭在与排出腔和吸入腔均不相通的中间部位螺旋槽，由于间隔一个螺距（T/2）的两条螺旋槽是相互密封隔离的，螺旋槽内的介质压力对从动螺杆产生的轴向力为零。所以，作用于一条螺旋槽的总轴向力为abcc′b′a和fghijkf面积之差乘以全压力p。由于从动螺杆螺旋头数为2，故作用于一根从动螺杆的总轴向力等于一条螺旋槽的总轴向力的两倍。

若abcc′b′a和fghijkf这两部分面积相等，则从动螺杆就不承受轴向力，因此也就不存在作用于螺杆的力矩。考虑到实际上从动螺杆旋转会产生摩擦，存在损失，故设计泵时就必须使abcc′b′a的面积略小于fghijkf的面积，这样就会产生负的力矩值，使从动螺杆实现自动旋转，只起“密封器”的作用。

必须指出，图3-21中e和f以及e′和f′两点之间是间断的，压力分界在这两点之间是不明确的，因此上述的轴向力计算会有一定的误差，只是这个间断的间距很小，可以忽略不计。实际上，由于螺杆螺旋在螺杆衬套孔内啮合时存在着各种必须的间隙，也会导致压力分界发生变化，这会与理论的分析有所出入。所以计算只是接近理论，这些误差影响很小，可以不予考虑。

由图3-21可以看出：齿形中心角2τ的大小直接影响到从动螺杆过流断面面积abcc′b′a的大小，所以改变2τ角就能改变介质作用在从动螺杆上的力矩。

（3）理想的齿形中心角2τ 理想的2τ角就是能使从动螺杆运行时产生自转力矩。由于图3-22中螺杆螺旋形成齿轮的啮合线所包围的面积A_fghijkf为

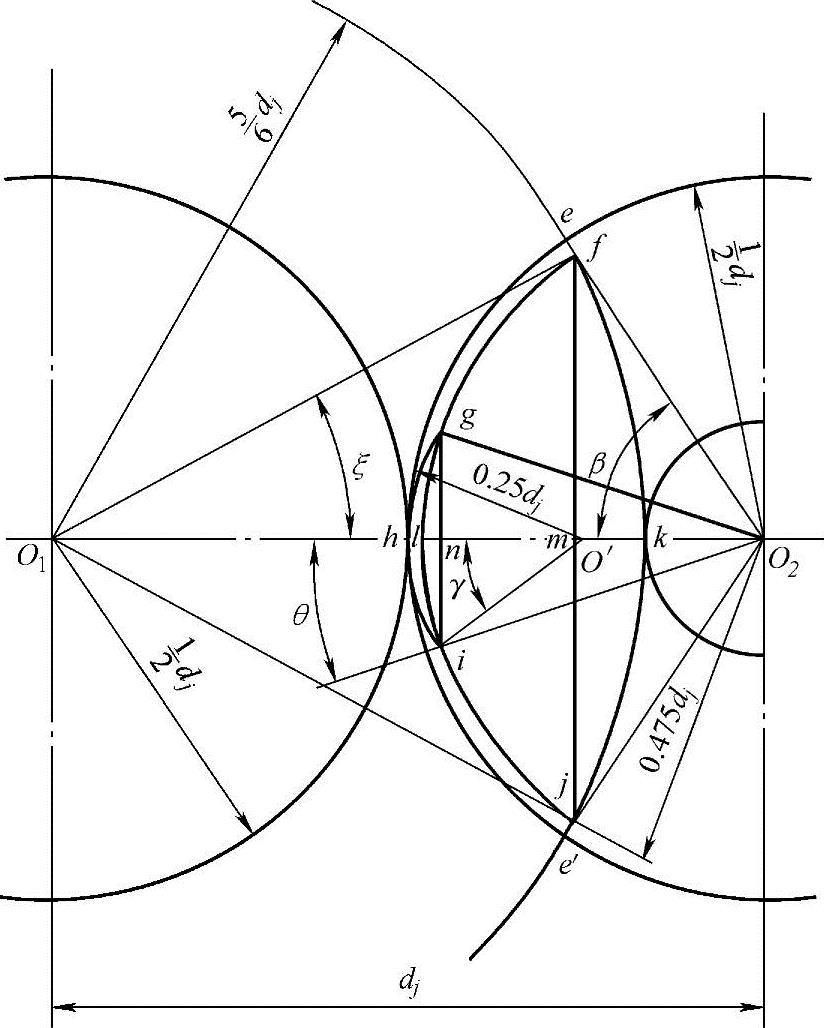
图3-22 螺杆螺旋形成齿轮的啮合线

A_fghijkf=A_fmjkf+A_fglijmf+A_ghilg （3-71）

由ΔO₁fm和ΔO₂fm可得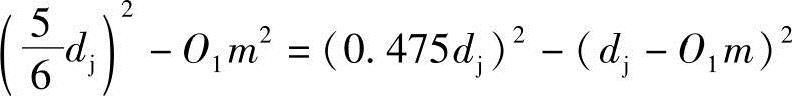

所以O₁m=0.73441d_j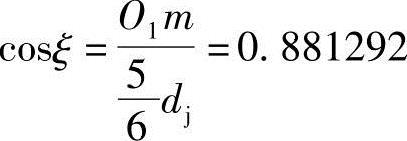，，ξ=28.201388°=0.492207rad

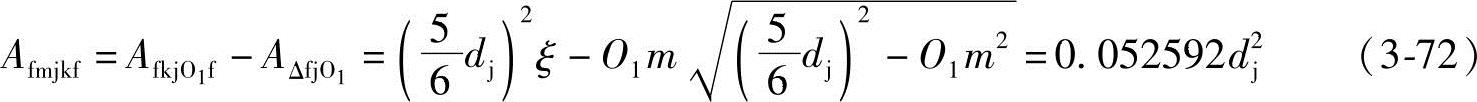
因为 O₂m=d_j-O₁m=0.26559d_j，，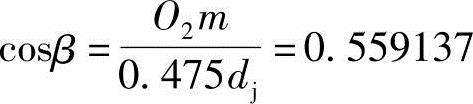

β=56.003874°=0.977452

所以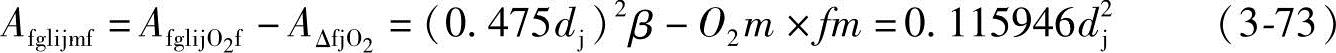

由ΔO′gn和ΔO₂gn可得（0.25d_j）2-O′n²=（0.475d_j）²-（O′n+0.25d_j）²，

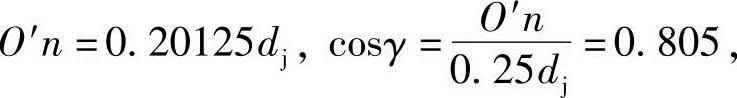
γ=36.389745°=0.635121rad，O₂n=O′n+0.25d_j=0.45125d_j，

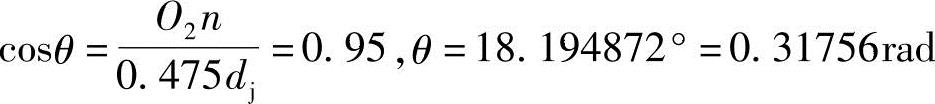
所以

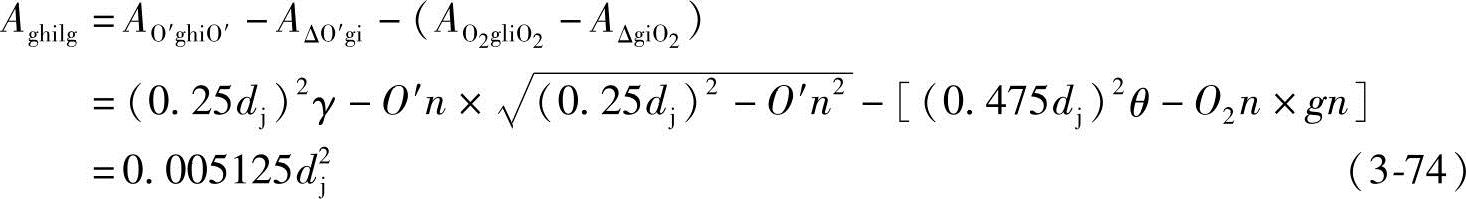
∴将式（3-72）、式（3-73）和式（3-74）代入式（3-71）得

A_fghijkf=0.173663d_j²

2A_fghijkf=0.347326d²_j （3-75）

对于螺杆螺旋头数为2，若按А.Е.Жмудь提出的齿形中心角2τ=0.18π=32°24′的修正齿形，可计算得A₃=0.428317d²_j，所以图3-21中过流断面面积A_abcc′b′a的值为

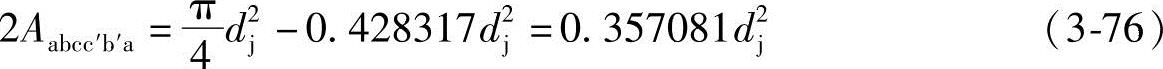(www.xing528.com)

作用于面积A_abcc′b′a的轴向力指向吸入腔，轴向力应为正值；作用于面积A_fghijkf的轴向力指向排出腔，轴向力应为负值。所以，作用于一根从动螺杆螺旋的总轴向力p_z2′由式（3-75）和式（3-76）可得

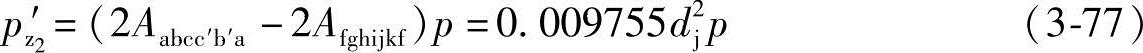
所以，由轴向力p_z2′产生的力矩M₂为

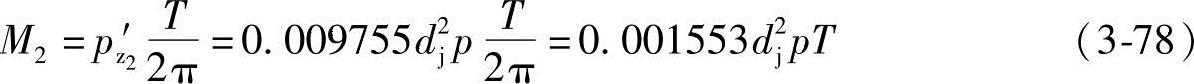
由式（3-77）得到的从动螺杆的力矩为正值，尽管M₂的值较小，但仍表示从动螺杆没有在介质作用下的自动旋转，M₂仍为对原动机的力矩起着相反作用的力矩，从动螺杆需要主动螺杆带动它旋转。作用于三根螺杆螺旋槽的总的轴向力等于过流断面面积A乘以全压力p。

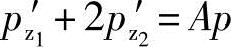
式中 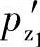——作用于主动螺杆螺旋槽的轴向力。

由式（3-60）和式（3-77）得作用于主动螺杆螺旋槽的轴向力p_z1′为

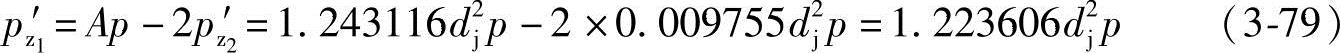
p_z1′为正值，表示该力的方向指向吸入腔。

故作用于主动螺杆螺旋槽的p_z1′轴向力产生的力矩M₁为

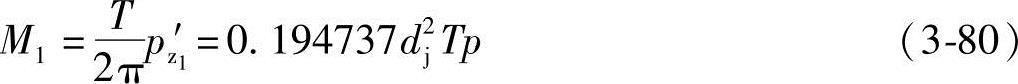
由式（3-78）和式（3-80）得三根螺杆上的力矩之和M为：

M=M₁+2M₂=0.194742d_j²Tp+2×0.001553d_j²Tp=0.197848d_j²Tp （3-81）

已知三螺杆泵的理论功率P_l等于泵的全压力p乘以理论流量Q_l，也等于理论力矩M_l乘以每秒角速度ω，故将式（3-62）代入后可得

式（3-81）的值和式（3-82）的值相同，说明作用在三根螺杆上的总力矩M，在理论上和泵的理论力矩M_l相等，这就证明了上述作用在螺杆上的力矩的计算是正确的。可见，2τ=0.18π的齿形中心角并不是理想的状况。

若要使从动螺杆具有自转力矩，M₂应为负值，也就是说要求A_abcc′b′a＜A_fghijkf。

由式（3-75）和式（3-76）知

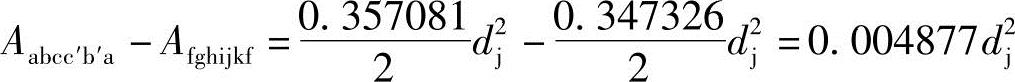
从图3-5可知，欲使A_abcc′b′a的值减小0.004877d²_j，只需从动螺杆螺旋的齿形中心角2τ所包含的螺旋槽的过流断面面积减少0.004877d²_j，所以减少的面积ΔA所对应的应减小的Δτ中心角为

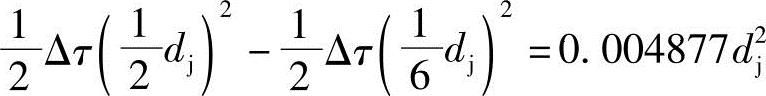
所以 Δτ=0.0438975=0.01397π

即必须使从动螺杆齿形中心角2τ＜0.18π-0.013973π=0.166027π=29°53′55″才可能得到M₂为负值，从动螺杆才能有自转力矩，才能真正起“密封器”的作用。之所以说“可能”是因为还需要考虑从动螺杆旋转时与介质的摩擦损失。M₂变为负值，说明在理论上从动螺杆是在介质压力所产生的力矩作用下旋转的。这个力矩促进主动螺杆转动并在主动螺杆上造成附加的力矩。所以说这个附加力矩不是工作力矩，因为是在主动螺杆——输送的介质——从动螺杆——主动螺杆的系统中为内力矩，并不影响外力矩，故是无效力矩。这也可从三根螺杆的总力矩M等于泵理论力矩M_l得出。在M₂为负值情况下，从式（3-81）可知，主动螺杆的力矩M₁大于三根螺杆的总力矩M，这个差值正好就是两根从动螺杆的自转力矩。主动螺杆的力矩M₁除了用来提高介质的压力外，还要克服介质对主动螺杆的反作用力矩，还有一小部分（M₂的值远小于M₁）则通过自转力矩去推动从动螺杆，克服从动螺杆旋转时的摩擦阻力。可见从动螺杆实际并不起多少作用，有效功是由主动螺杆完成的。

由上可知，若采用“四等分”的2τ=34°23′32″的修正齿形，虽然对泵的流量没有影响，但因M₂为正值，且大于2τ=0.18π=32°24′时的M₂值，也就是说主动螺杆需用比2τ=0.18π时更多的力矩去推动从动螺杆旋转。这个差值就是实际多消耗的机械损失，换言之，其机械效率比2τ=0.18π时泵的机械效率还要低，因此这类泵更不理想。

（4）错误采用2τ=0.18π齿形的原因 在介绍三螺杆泵的螺杆旋转特点时，提出从动螺杆并不是由主动螺杆带动旋转，而是由介质推动下旋转的。上面的推导却证明了对于实际使用的“标准”螺杆齿形中心角2τ=0.18π的情况又并非如此。从下面的推导可以说明这一错误产生的原因。下面先推导齿形未作修正的2τ=0.18π的理论从动螺杆的情况。

与从动螺杆螺旋修正齿形不同的是：从动螺杆的理论齿形螺旋啮合线所围的面积不是图3-21中的A_fghijkf，而是图3-19中的A_abcda。而且从动螺杆一条螺旋槽的过流断面面积不是图3-21中的A_abcc′b′a，而是图3-3中2A_{c′b′a′c}（图中只画出了1/2的过流断面A_{c′b′a′c}，故需乘以2），因此，图3-5中的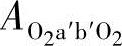应为图3-3中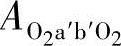。过流断面其余的各组成部分不变。由式（3-56）知，图3-5中的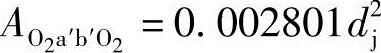，经相似的计算，可得图3-3中的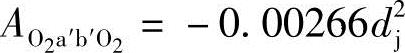，因此图3-3中的2A_{c′b′a′c}=0.184675d²_j。

由此可知，理论齿形的从动螺杆螺旋槽受到的总轴向力p_z′₂等于2倍的一条螺旋槽过流断面面积（图3-3中的2A_{c′b′a′c}）和2倍的啮合线包围的面积（图3-19中的A_abcda）之差乘以介质全压力p，即

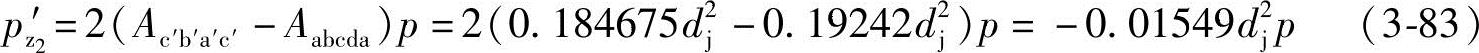
轴向力p_z2′产生的力矩M₂为

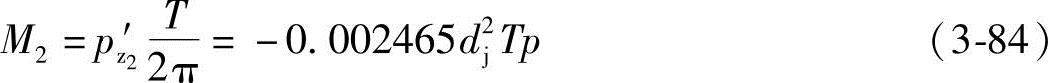
从动螺杆的力矩为负值，说明理论齿形的从动螺杆是有自转力矩存在，这与对三螺杆泵螺杆旋转的要求相符。

与式（3-60）求修正齿形的螺杆螺旋工作长度上的过流断面面积A的方法相似，可求得理论齿形的螺杆工作长度上的过流断面面积A=1.2525d²_j。

由于作用在三根螺杆螺旋凹槽的总轴向力等于过流断面面积A乘以全压力p，故可求得理论齿形的主动螺杆螺旋槽的轴向力p_z1′为

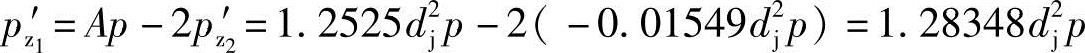
所以，主动螺杆螺旋槽的轴向力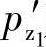产生的力矩M₁为

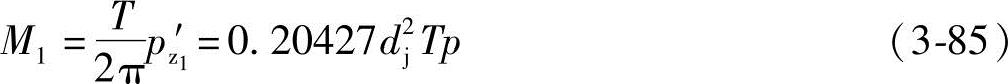
由式（3-84）和式（3-85）得三根螺杆的力矩之和M为

M=M₁+2M₂=0.204272d_j²Tp+2（-0.002465d_j²Tp）=0.199342d_j²Tp （3-86）

已知三螺杆泵的理论功率P_l等于泵的全压力p乘以理论流量Q_l，也等于理论力矩M_l乘以每秒角速度ω：

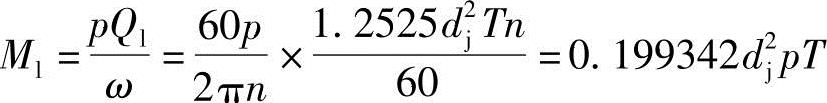
得到的结果与式（3-86）值相同，证明了上述的推导是正确的。

可见，当三螺杆泵螺杆螺旋为2τ=0.18π的理论齿形时，从动螺杆确实并不是由主动螺杆带动旋转，而是由介质推动，只起“密封器”的作用。在这种情况下主动螺杆和从动螺杆之间是不会存在相互的作用，因此也不会磨损。由于本章第四节中阐述的种种原因，从理论上解释了从动螺杆螺旋齿形在长幅外摆线齿顶圆处的锐角必需进行修正。正如上面所证明了的2τ=0.18π的理论齿形在修正后M₂变成了正值，这时的齿形就变得不理想了。实际上，即使选取的齿形中心角2τ能使M₂为负值，在泵起动和停车时，螺杆的窜动等种种原因，螺杆之间相互作用依然会存在。由此证明了修正从动螺杆的理论齿形是十分必要的。

我国的三螺杆泵行业大部分采用2τ=0.18π的齿形中心角（也有的采用“四等分”2τ=0.1911π=34°23′32″的齿形中心角）。其主要原因是因为我国的三螺杆泵最早是仿制前苏联的产品，自行设计也是依据前苏联А.Е.Жмудь的著作。而在他的著作中对＜1∶3∶5型＞的三螺杆泵是将2τ=0.18π=32°24′作为标准齿形，他推导得出从动螺杆轴向力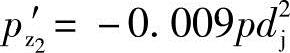，他据此得到的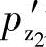为负值，作为得出介质作用在从动螺杆螺旋槽的轴向力指向排出腔、作为存在自转力矩结论的依据。从表面看，若不考虑假设的轴向力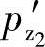的方向，即不考虑正负的话，这一结果在数值上似乎与笔者推导得出的式（3-77）的结果差别很小。但是这一差别并非是计算误差所致。笔者认为这是А.Е.Жмудь在推导计算的过程中出了错。错误地将图3-21中理论齿形啮合线所围的面积A_ehe′ke来代替修正齿形啮合线所围的面积A_fghijkf，于是将A_ehe′ke和A_fghijkf这两部分面积之和来代替2倍的A_fghijkf的面积，得出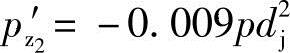的错误结果！这就是其出现错误的原因。

由此可知，我国目前许多制造厂生产的三螺杆泵，无论螺旋的齿形中心角2τ取0.18π还是“四等分”都不是理想的齿形。考虑到实际上从动螺杆旋转时存在着与介质的摩擦损失，理论上理想的2τ应小于0.166027π。但也并非2τ取得越小就越好，由于从动螺杆螺旋的齿形是“收口”的，加工时若螺杆的螺旋角越小，则2τ越小，就越容易发生“干涉”，设计泵时选取导程的范围也就缩小。故建议2τ取0.16π即28°48′为宜或可再略小一些。