如何计算泵内工作长度段的过流断面面积A？

（1）螺杆衬套孔的横截面面积A₃ 由图3-19可知，螺杆衬套孔的横截面面积A₃是以主动螺杆螺旋外径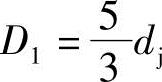为直径的圆面积加上两个以从动螺杆外径d_j为直径的圆面积，再减去两块abcda“凸镜”的面积2A_abcda：

即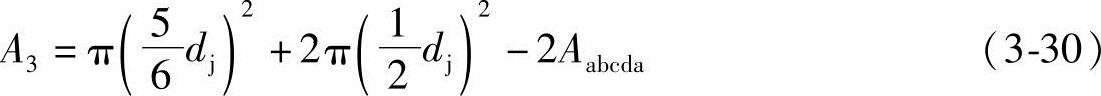

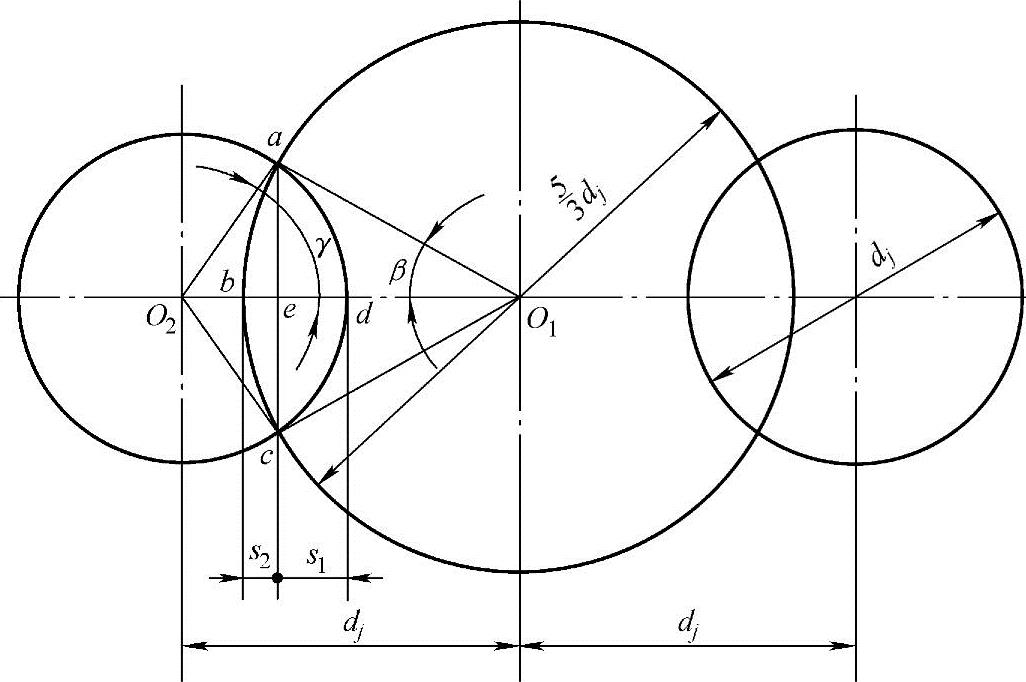
图3-19 螺杆衬套横截面的过流断面面积

由图3-19得

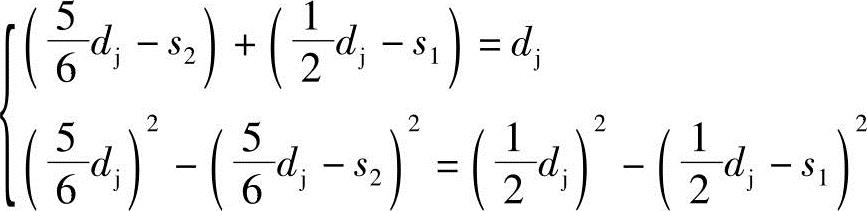
所以，解得，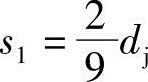

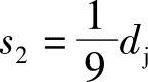
因为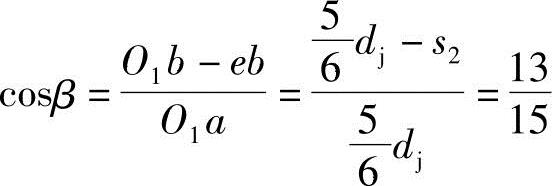

所以得 β=29.926435°=0.522315，sinβ=sin29.926435°=0.498888

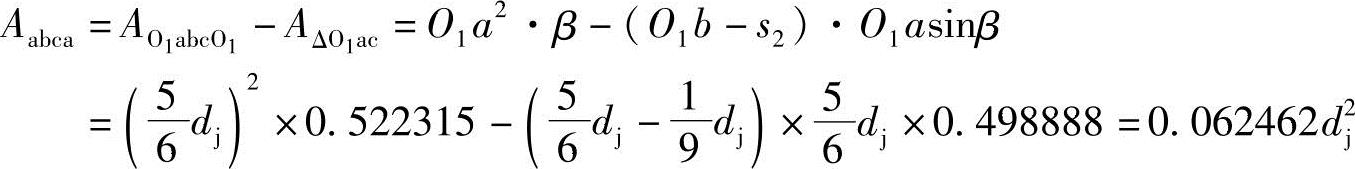
因为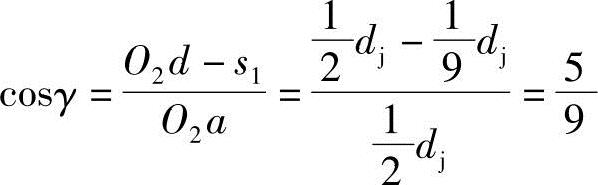

所以 γ=56.251011°=0.981765rad，sinγ=0.831479

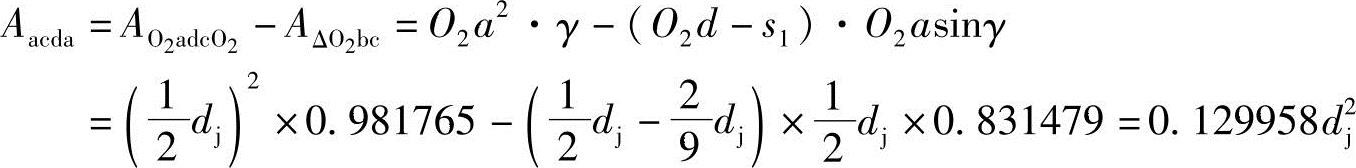
所以 A_abcda=Aabcd-^Aacda=0.062462d_j²+0.129958d²_j=0.19242d_j²（3-₃1）

将式（3-31）代入式（3-30）得

所以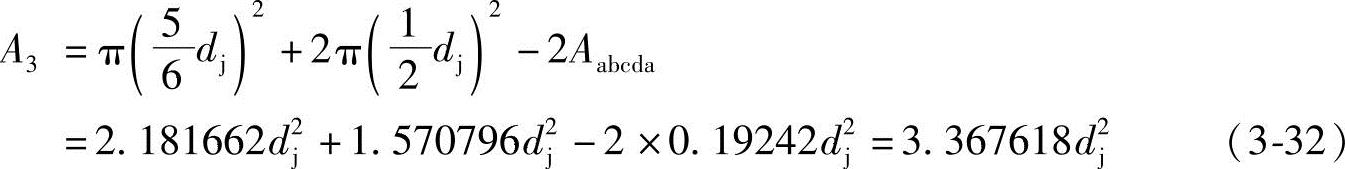

（2）主动螺杆螺旋齿形横截面面积A₁ 由图3-5可知，主动螺杆螺旋齿形横截面面积由2倍的齿顶圆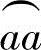构成的扇形面积A_θaa，2倍的齿根圆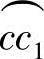构成的扇形面积A_θcc1，以及4倍的以b点为分界的短幅外摆线ab和外摆线bc构成的齿形曲线扇形面积A_θab和A_θbc之和。

即 A₁=2A_θaa+2A_θcc1+4A_θab+4A_θbc （3-33）

1）面积A_θab。由图3-4可知，r_b为从动螺杆螺旋齿形横截面上由半径为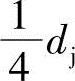的动圆和半径为0.475d_j的圆弧的交点。由式（3-4）已知r_b=0.568441d_j

图3-5中齿形曲线ab构成的扇形面积A_θab为曲线ab和曲线两端a点及b点的两个半径的矢量所限制的面积，按微分几何的方程可知：

式中 ρ——曲线ab上任意点的半径矢量，ρ²=x²+y²；

θ_a和θ_b——曲线ab的积分极限；

θ——极角，。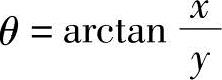

由式（3-5）知，X和Y是Φ的函数：

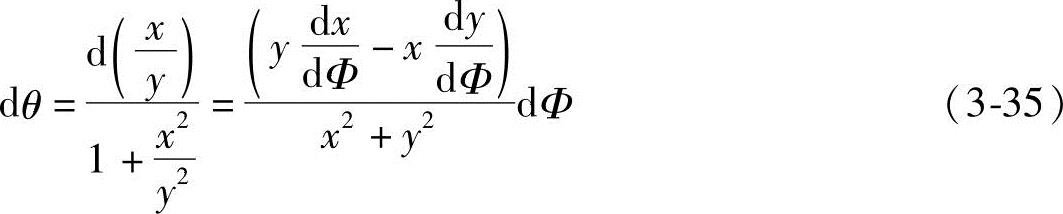
将式（3-35）代入式（3-34）得

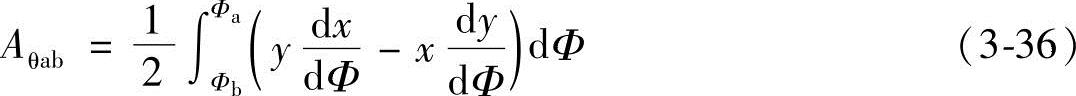
将式（3-5）的x和y分别对Φ求导，得

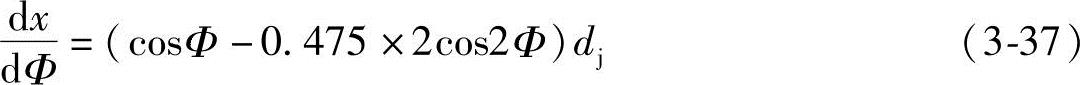
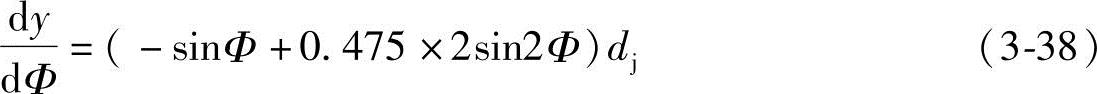
将式（3-5）、式（3-37）和式（3-38）代入式（3-36）得

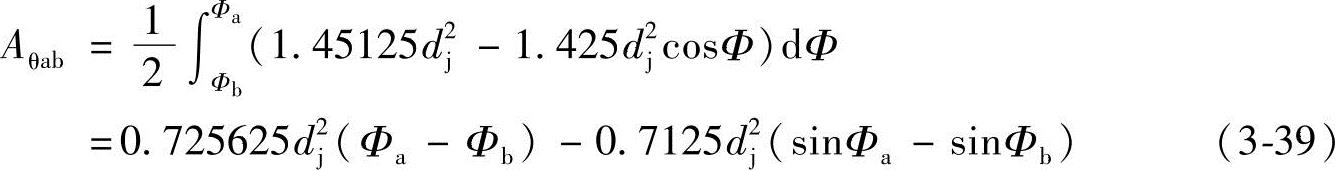
由图3-4知，曲线ab的半径矢量ρ是由O₁b变化至O₁a，即由式（3-4）知ρb=0.568442d_j至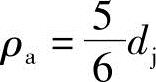的范围内变化。

ρ²=x²+y²=d²_j+0.475²d²_j-2×0.475d²_jcosΦ=1.225625d²_j-0.95d²_jcosΦ

即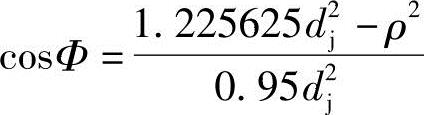

所以，由ρ的边界值可求得Φ的边界值

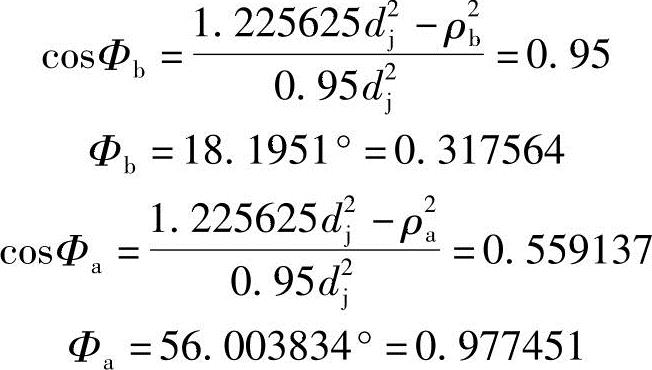
由式（3-5）得：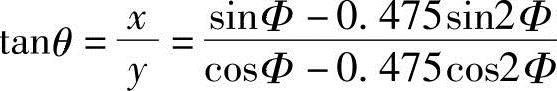

由Φ的边界值可得θ的边界值

cos2Φ=cos36.3902°=0.804995

sinΦ_b=cos18.1951°=0.312254

sin2Φ_b=cos36.3902°=0.593281

所以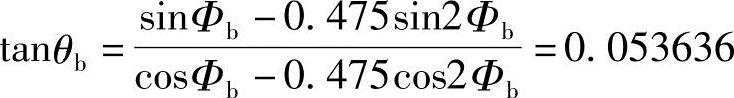

θ_b=3°04′13″=3.0702°=0.053559rad （3-40）

sinΦ_a=sin56.003834°=0.829075

sin2Φ_a=sin112.007668°=0.927134

cos2Φ_a=cos112.007668°=-0.374731

所以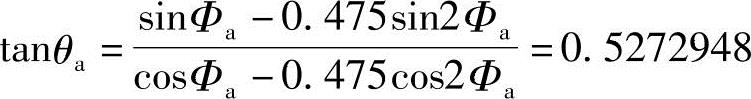

θ_a=27°48′14″=27.8024°=0.485244rad （3-41）

将求得的Φ_a、Φ_b、sinΦ_a和sinΦ_b值代入式（3-39）可得

A_θab=0.725625d²_j（Φ_a-Φ_b）-0.7125d²_j（sinΦ_a-sinΦ_b）=0.110596d²_j （3-42）

2）面积A_θbc。图3-5中齿形曲线bc构成的扇形面积A_θbc为曲线bc和曲线两端点b和c的两个矢量半径所限制的面积，按微分几何的方程可知：

式中 ρ——曲线bc上任意点的半径矢量；

θ_b和θ_c——曲线bc的积分极限。

由式（3-6）知，x和y是Φ的函数，即得式（3-35）。(www.xing528.com)

将式（3-35）代入式（3-43）得

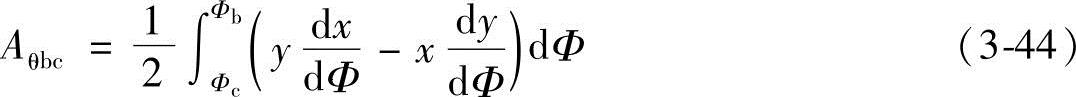
将式（3-6）的x和y分别对Φ求导，得

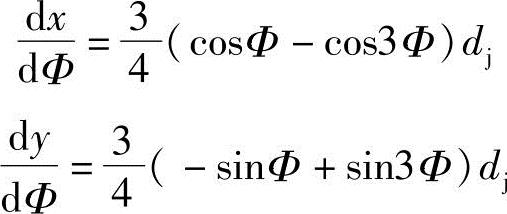
代入式（3-44）可得

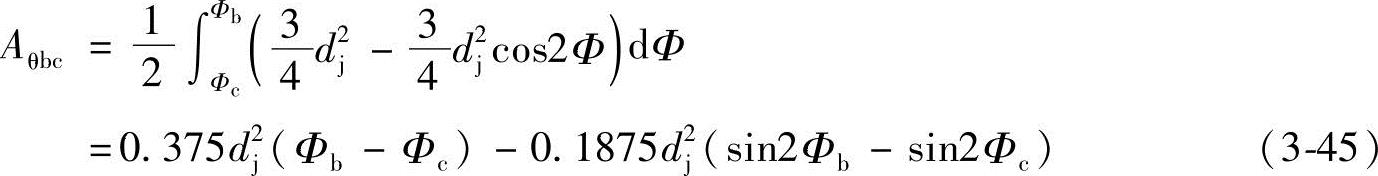
由图3-4可知，曲线bc的半径矢量ρ是由O₁c变化至O₁a，即由ρ_b=0.5d_j至ρ_b=0.568442d_j的范围内变化。

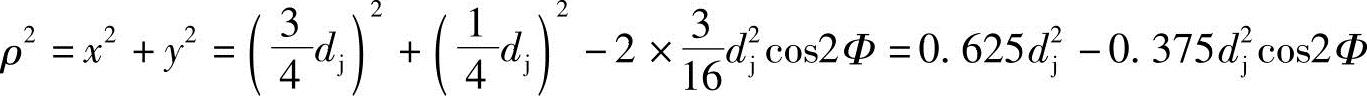
即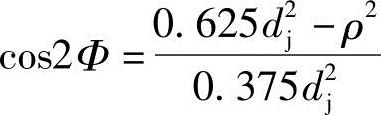

由ρ的边界值可求得Φ的边界值

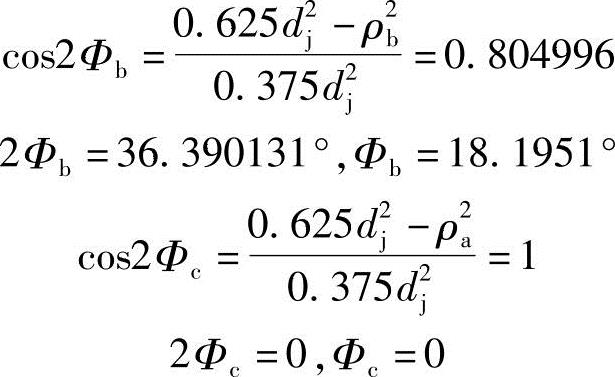
由式（3-6）得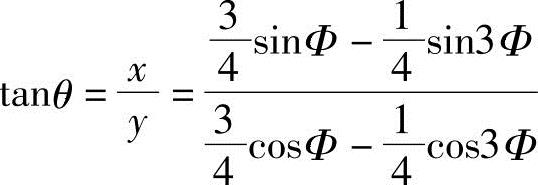可由Φ的边界值求得θ的边界值

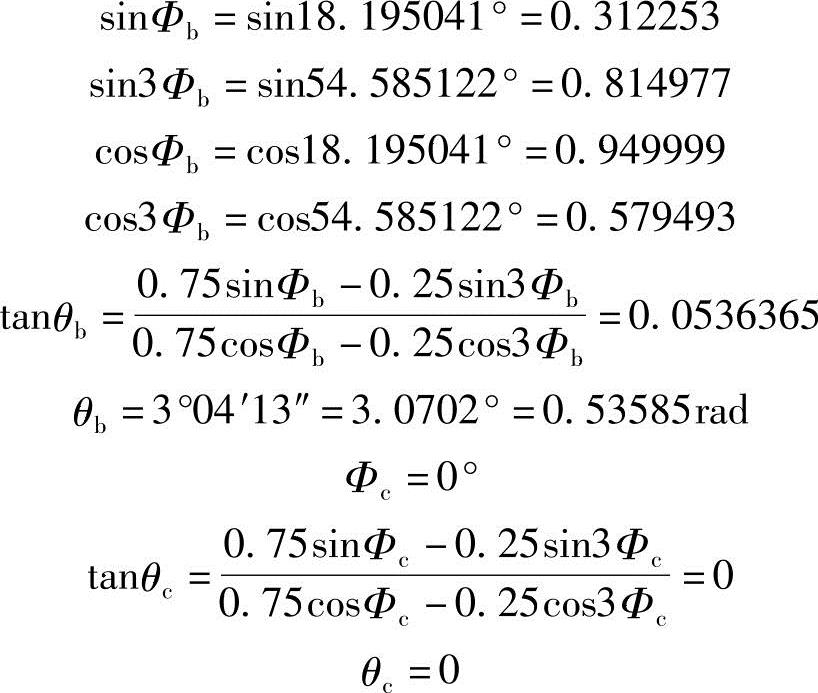
将求得的Φ_b和Φ_c值代入式（3-45），得

A_θbc=0.375d²_j（Φ_b-Φ_c）-0.1875d²_j（sin2Φ_b-sin2Φ_c）=0.007846d_j²（3-46）

3）面积A_θaa。由图3-5可知，齿顶圆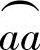构成的扇形面积A_θaa为

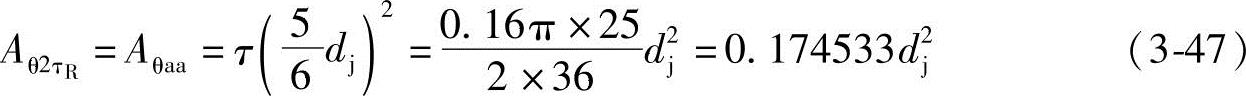
4）面积A_θcc′。由图3-5可知，齿根圆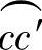构成的扇形面积A_θcc′为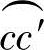圆弧所对中心角∠cO₁c′为

∠cO₁c′=π-（2∠cO₁a+2τ）=π-（2θ_a+2τ）=π-（2×0.485244+0.16π）=1.66845

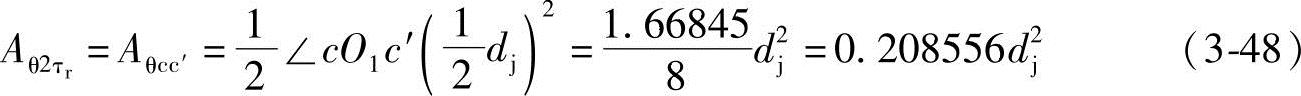
将求得的式（3-42）、式（3-46）、式（3-47）和式（3-48）的值代入式（3-33）得

A₁=2A_θaa+2A_θcc₁+4A_θab+4A_θbc=1.239946d²_j （3-49）

（3）从动螺杆螺旋齿形横截面面积A₂ 由图3-5可知，从动螺杆螺旋齿形横截面面积A₂，由2倍的齿顶圆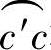构成的扇形面积A_θcc′，2倍的齿根圆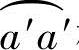构成的扇形面积A_θa′a′，以及4倍的以b点为分界的长幅外摆线a′b′构成的扇形面积A_θa′b′之和。因为径向直线段b′c′仅成为a′b′曲线的一个边界位置（即b′点），不构成面积。

所以 A₂=2A_θc′c+2A_θa′a′+4A_θa′b′ （3-50）

1）面积A_θa′b′。由图3-5可知，齿形曲线a′b′构成的扇形面积为曲线a′b′和曲线a′点及b′点的两个半径的矢量所限的面积，与主动螺杆相仿，即

与前相同

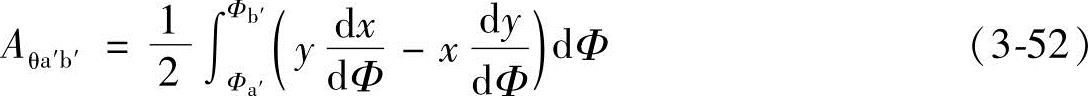
将式（3-9）的X和Y分别对Φ求导后，得

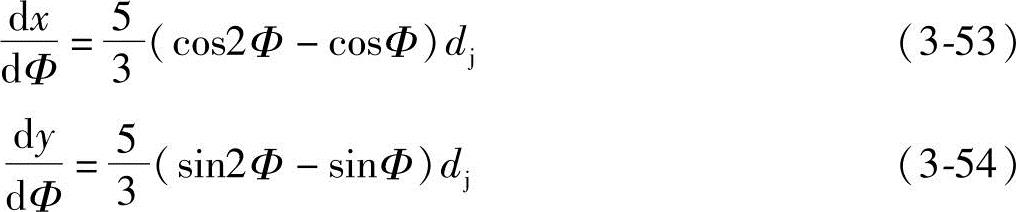
将式（3-9）、式（3-53）和式（3-54）代入式（3-52），可得

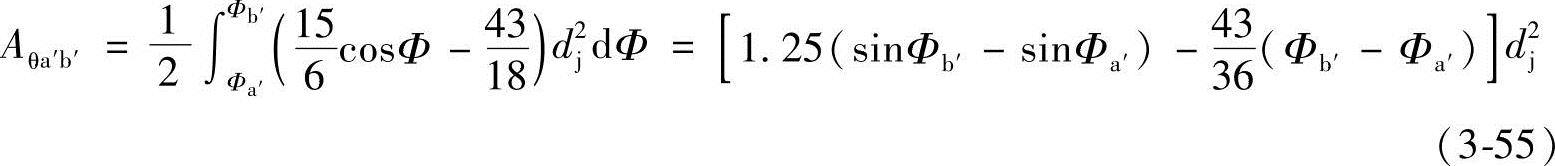
由图3-5可知，曲线a′b′的半径矢量ρ是由O₂a′变化至O₂b′，即由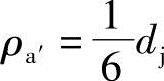至ρ_b′=0.475d_j的范围内变化。

因为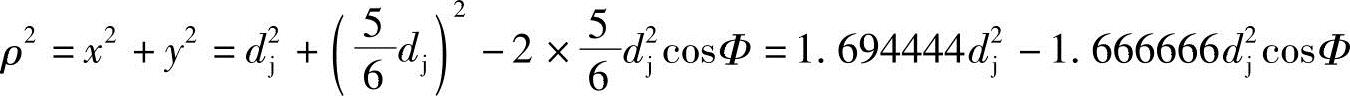

即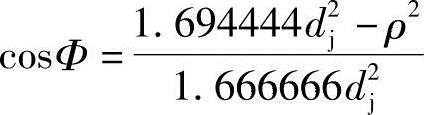

由ρ的边界值可求得Φ的边界值

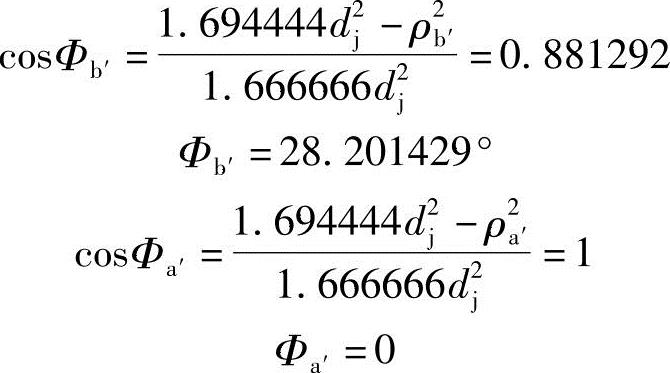
因为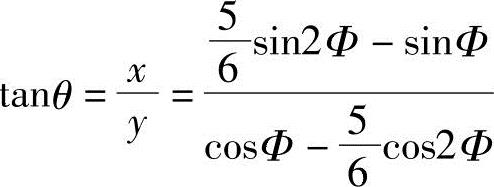

由Φ的边界值Φ_b′和Φ_a′可求得θ的边界值

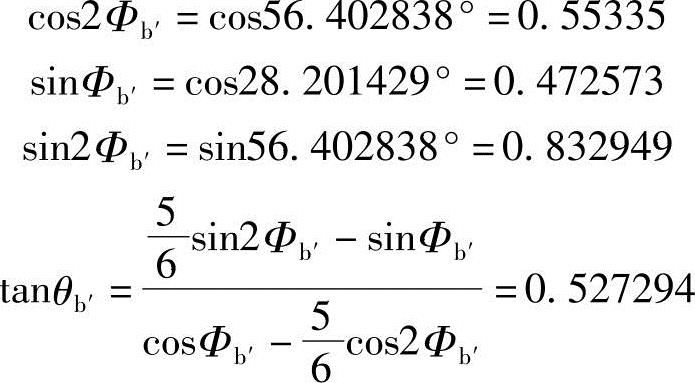
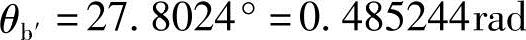
因为sinΦ_a′=sin2Φ_a′=0、cos2Φ_a′=1

所以 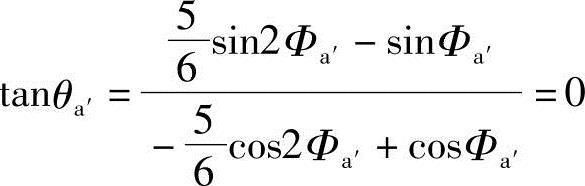，θ_a′=0

将求得的Φ_b′、Φ_a′、sinΦ_b′和sinΦ_a′代入式（3-55），得

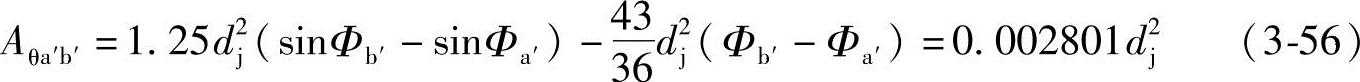
2）面积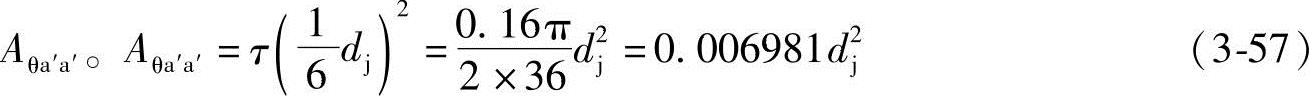

3）面积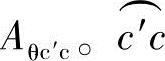圆弧所对的中心角∠c′O₂c为

∠cO₂c′=π-（2∠cO₂a′+2τ）=π-（2θ_b′+2τ）=π-（2×0.485244+0.16π）

=1.66845rad

由图3-5可知，齿顶圆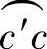构成的扇形面积A_θc′c为

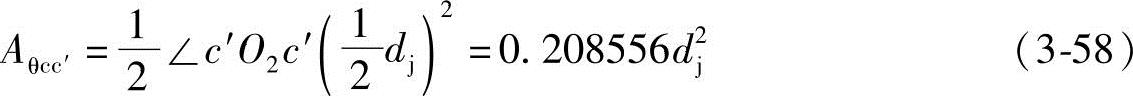
将式（3-56）、式（3-57）和式（3-58）代入式（3-50）得

A₂=2A_θc′c+2A_θa′a′+4A_θa′b′=0.442278d²_j （3-59）

（4）工作长度段的过流面面积A 由图3-19和图3-5，并将式（3-32）、式（3-49）和式（3-59）代入

A=A₃-A₁-2A₂

可得A=3.367618d_j²-1.239946d²_j-2×0.442278d²_j=1.243116d_j² （3-60）