修正后的主动螺杆螺旋齿形曲线探究

从动螺杆螺旋以圆弧修正理论齿廓的锐角后，根据啮合原理，主动螺杆螺旋相应修正的齿形曲线可用全部都是圆的包络线来求得。此方法较为复杂，仅用齿廓法线的方法作简要介绍。

如图3-7所示，选取两个动坐标系：一个与主动螺杆的坐标系O₁X₁Y₁固连；另一个与从动螺杆坐标系O₂X₂Y₂固连。

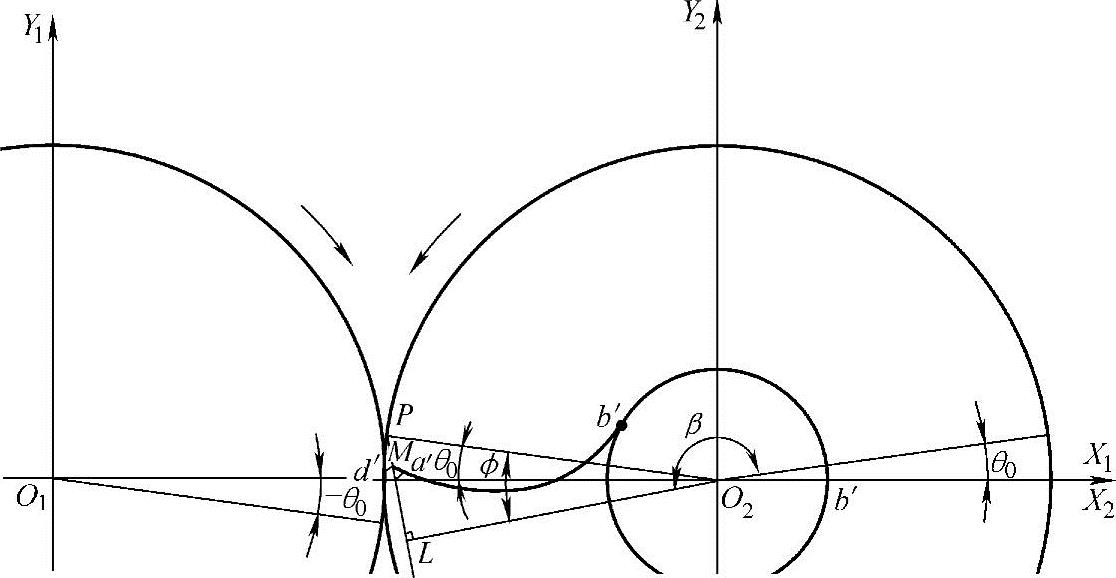
图3-7 修正主动螺杆齿形曲线的形成

若从动螺杆转动θ₀角时，主动螺杆也相应地转动负θ₀角，则两个坐标系的坐标变换为

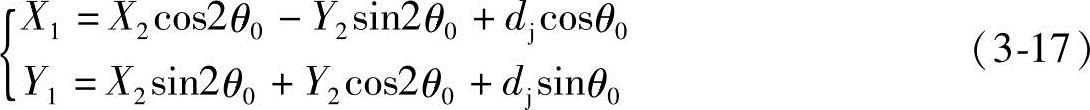
由式（3-15），从动螺杆的修正圆弧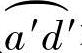在图3-7中O₂X₂Y₂坐标系的方程为

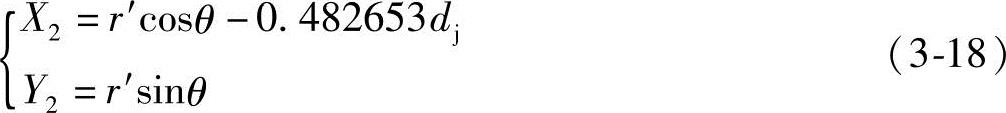
θ角的区间为62°53′44″≤θ≤180°。

设M（X₂，Y₂）为从动螺杆螺旋修正圆弧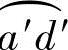上的任意一点，P点为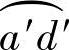在M点的法线与从动螺杆螺旋齿顶圆的交点。从从动螺杆坐标原点O₂向MP直线作垂线，交于L，X₂轴和O₂L的夹角为β，∠PO₂L为Φ，∠PO₂d′为θ₀。根据齿轮啮合原理可知，当从动螺杆转动θ₀角时，P为啮合节点，此时M点与主动螺杆螺旋的齿形曲线相啮合。

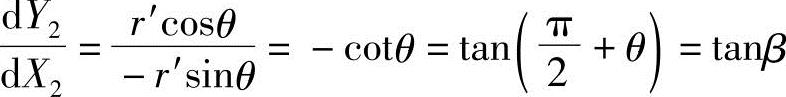
式中 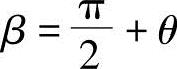(www.xing528.com)

又向量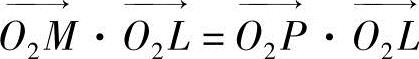

即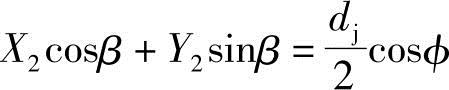

故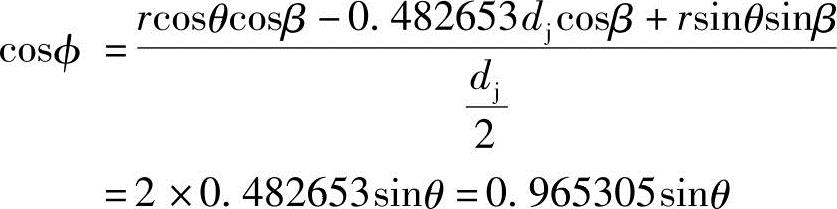

由初始条件θ=180°，则cosφ=0，即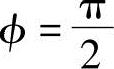

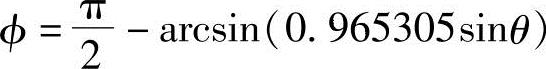
θ₀=π-（β-φ）=π-θ-arcsin（0.965305sinθ） （3-19）

将式（3-18）代入式（3-17），得式（3-20）并与式（3-19）联立，解得修正后的主动螺杆螺旋的齿形曲线方程式

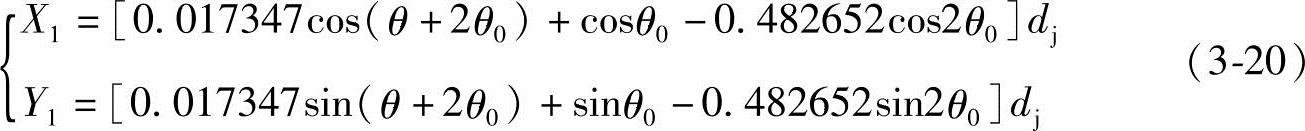
θ₀=π-θ-arcsin（0.965305sinθ）

（62°53′44″≤θ≤180°）

主动螺杆螺旋修正后的齿形曲线，由于是圆的包络线，故图3-4中主动螺杆螺旋齿形abc曲线修正后与齿根圆的相交处不再像图3-4中的c点那样构成角度，而是圆滑相接。解决了用径向直线修正从动螺杆螺旋齿形曲线带来的缺点。