【摘要】：由上所知，主动螺杆螺旋横截面的形状由图3-4中的齿形曲线abbc（外摆线）以及齿根圆弧和齿顶圆弧构成。圆弧可以看作是特殊的外摆线，所以主动螺杆螺旋型面的齿廓也可以说是由摆线组成的。由于ΦM=2Φ所以，主动螺杆齿形曲线bc的方程式为式（3-5）和式（3-6）均由第一章第四节的图1-2和图1-3推得。
由上所知，主动螺杆螺旋横截面的形状由图3-4中的齿形曲线ab（短幅外摆线）bc（外摆线）以及齿根圆弧和齿顶圆弧构成。圆弧可以看作是特殊的外摆线，所以主动螺杆螺旋型面的齿廓也可以说是由摆线组成的。
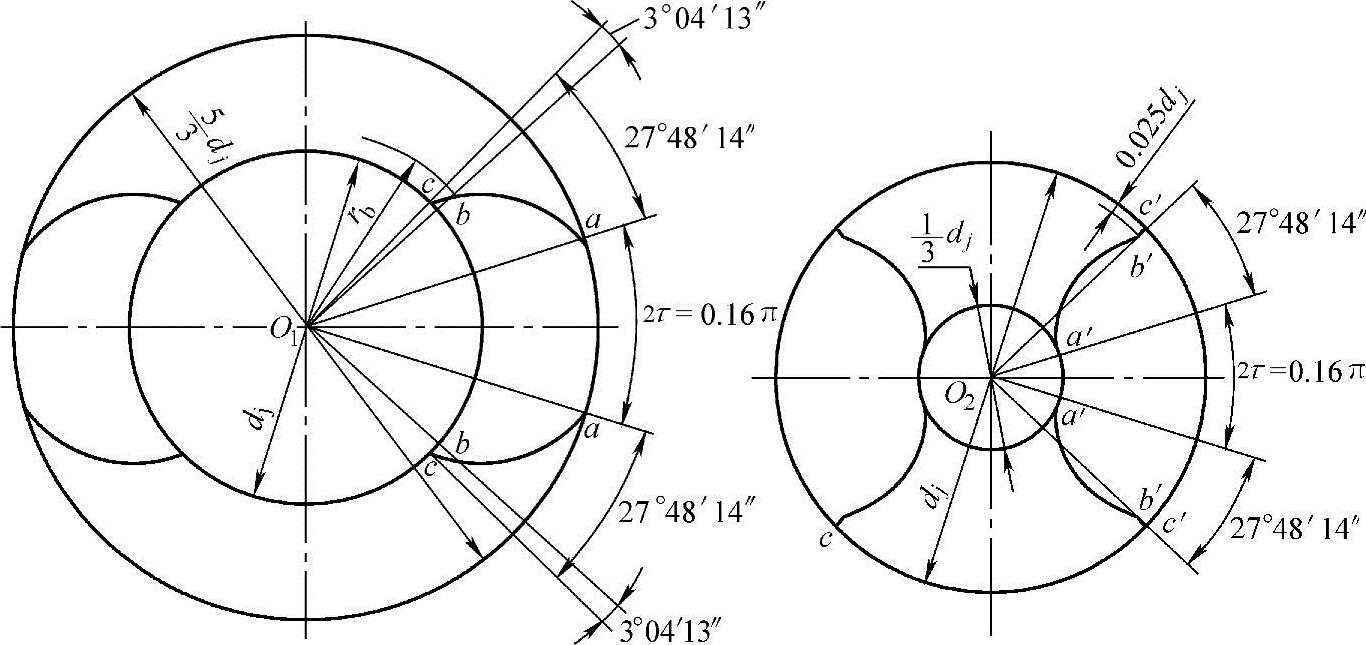
图3-5 以径向直线修正从动螺杆螺旋的齿形曲线
1）齿形曲线ab的方程式：
由式（1-24）短幅外摆线的方程式：
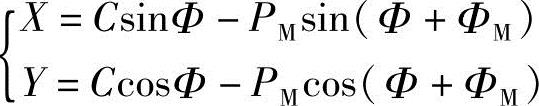
式中 C=dj，PM=0.475dj，Φ=ΦM
所以，主动螺杆齿形曲线ab的方程式为
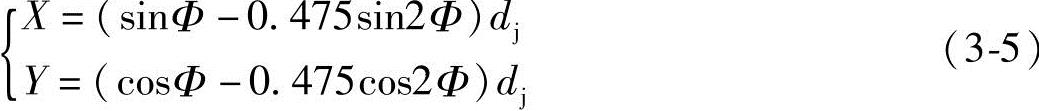
2）齿形曲线bc的方程式。
由式（1-10），外摆线的方程式为
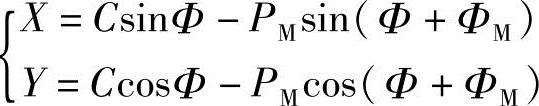(www.xing528.com)
由上述bc摆线的形成知，定圆直径为dj，动圆直径为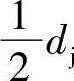
，动圆上的一点为摆点，式中，
，
。
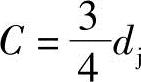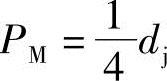由于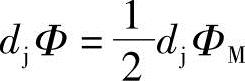 
ΦM=2Φ
所以，主动螺杆齿形曲线bc的方程式为
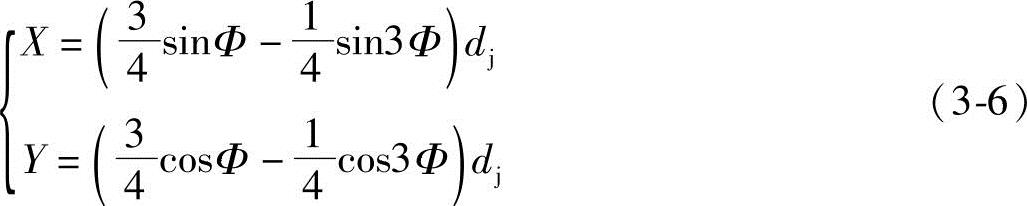
式（3-5）和式（3-6）均由第一章第四节的图1-2和图1-3推得。若X轴和Y轴设置在不同的位置以及动圆沿着定圆滚动的方向不同，则上述方程式的表达形式，诸如sin和cos，以及方程式中各项的符号会有变化。有的文献假设动圆的圆心O1在滚动起始时位于X轴上，其摆点的滚动起始位置也在X轴上，动圆沿定圆作逆时针滚动，则上述方程式的表达形式会与式（3-5）和式（3-6）有所不同，由于这种形式在一些文献中也常出现，故也作如下介绍：
齿形曲线ab段的方程式式（3-5）可表达为
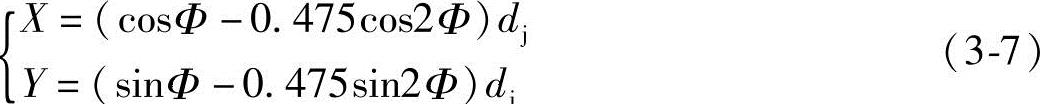
齿形曲线bc段的方程式式（3-8）可表达为
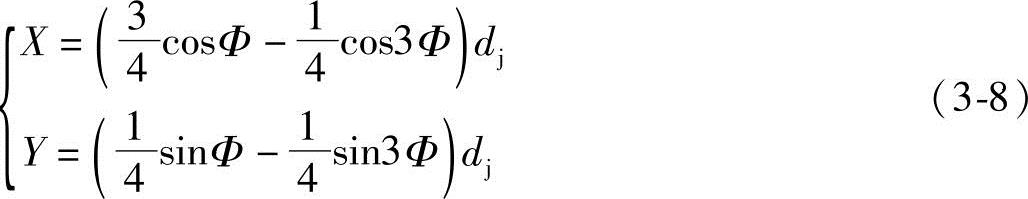
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
