密封性分析方法及应用实例

若将转子轴截面方程式式（2-4）中的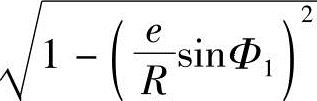用牛顿二项式展开，略去1以后的各项代入式（2-3），则式（2-18）中的Y成为如下近似表达式

Y=R+ecos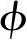₁=R+ecos2θ₀ （2-19）

式（2-19）对绘取轴截面图来说已足够精确。

把转子和定子的轴截面齿形曲线画在同一Y-_Z坐标中，并重叠在一起（图2-9）。考虑到转子中心线和定子中心线的位移为e，则在该轴截面图上，以定子中心线为Z轴时，由式（2-19）和式（2-16）可得转子和定子的坐标值Y的差ΔY₁和ΔY₂为

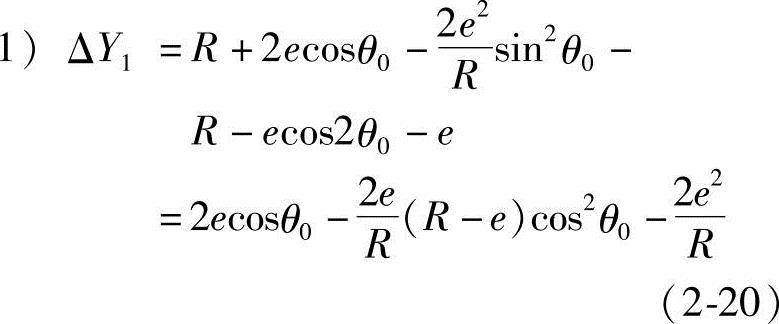
所以，当转子和定子的轴截面齿形重叠时，若两者存在着接触点或接触线，则必然为ΔY=0，

所以，由式（2-20）得

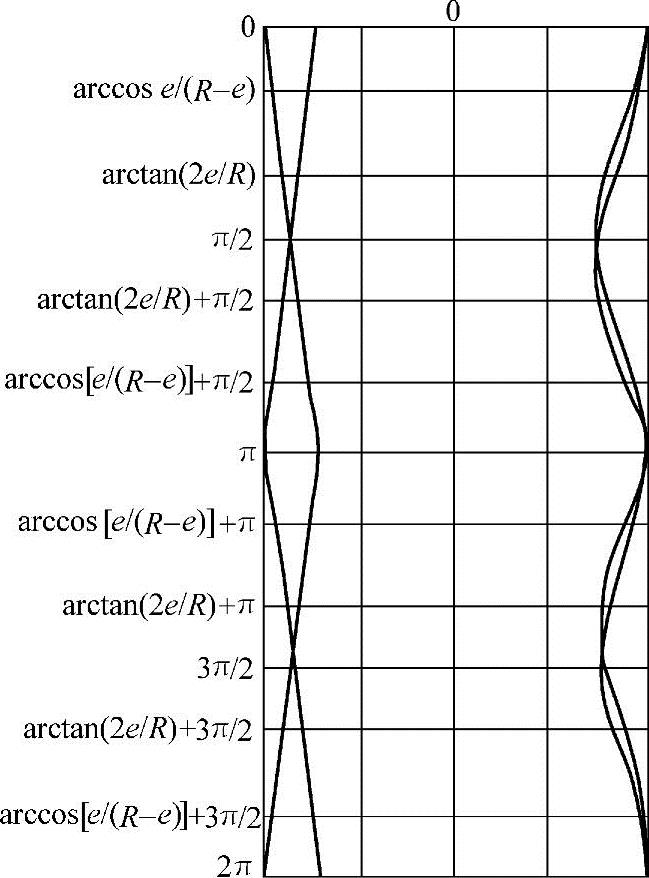
图2-9 转子和定子的轴截面齿形曲线重叠图形

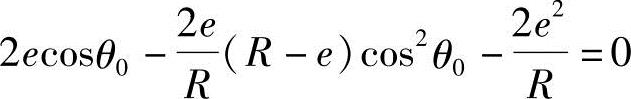
即

可见当cosθ₀在最小值和最大值区间时，即θ_0max至θ_0min区间时，两齿形曲线在该区间完全接触。

所以，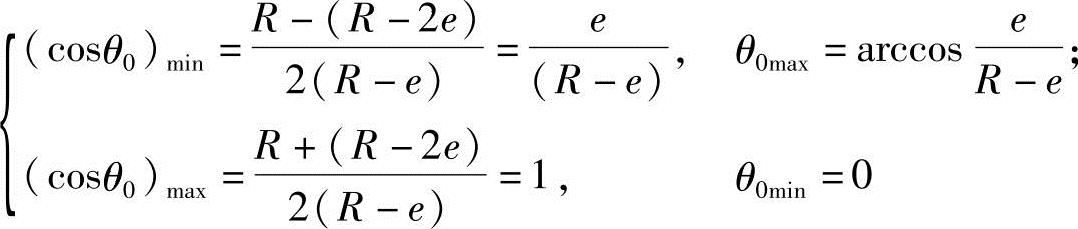

即当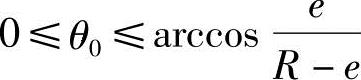时，转子和定子的齿形曲线完全重合；从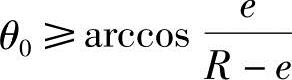起，两条曲线分离，此时定子的齿形曲线为直线段。

2）

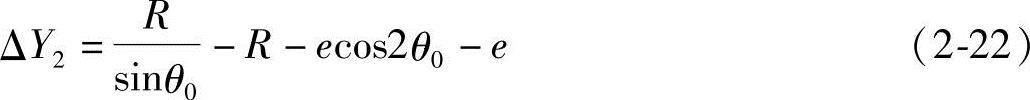
就是说当时有式（2-22），在齿形曲线直线段时转子和定子的接触点也即ΔY₂=0，

因为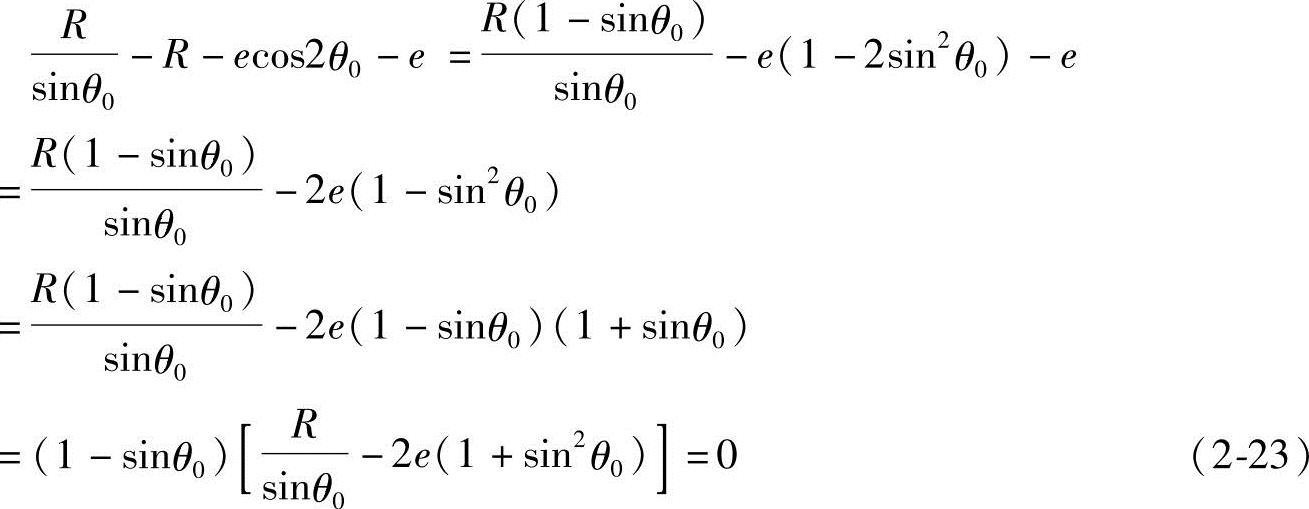

由式（2-23）可知，其解有两个。(www.xing528.com)

第一个解为 （1-sinθ₀）=0，即sinθ₀=1，θ₀=π/2。

此解表示：当θ₀=π/2时，转子和定子的齿形曲线重合。

第二个解为 ，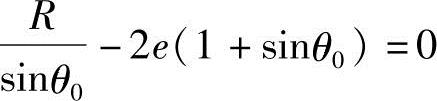

即 R-2esin²θ₀-2esinθ₀=0

所以，sinθ₀无意义。

此解表示：在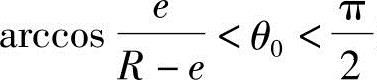区间时，转子和定子的齿形曲线不重合。由上可知：在一个导程T的轴截面区间内，转子和定子的不重合区间为

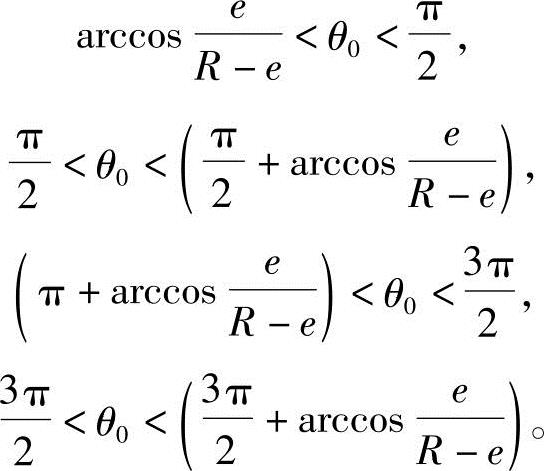
依据上述推导，就可绘出定子和转子的轴截面齿形重叠图形，如图2-9所示。

从图2-10转子和定子的端面齿形啮合可以看出，当转子在定子的内螺旋孔内转动时，转子和定子的啮合线只是在两个半径为R的半圆弧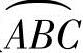和F存在。转子和定子的齿形曲线在这两个半圆弧的区间完全重合，在其他位置均为点啮合。当转子和定子在两直线段CD和FA相啮合时，即可得如图2-10所示的点a和b相仿的一系列啮合点。由此结合式（2-21）和式（2-22）得到的结论，可得到转子和定子在导程T范围内的啮合线和啮合点。

在此不再赘述轴截面上转子和定子的密封线的绘制过程，仅将结果表示在图2-11上。在导程T的范围内，其各端面的啮合点和啮合线显然是连续的，将各端面上的啮合点在轴截面上连起来，就得到图2-11中由直线和虚线表示的啮合线。可以看出，由啮合线形成的密封腔在理论上是完全密封的，即密封腔能将吸入室和排出室完全隔开，其密封性非常好。但在实际上，转子和定子心轴的加工总会存在误差；对于非橡胶的定子，转子和定子之间必需存在一定的间隙；而对于橡胶为材质的定子，在压制时由于配方和橡胶收缩时的不均匀性等因素，也会造成定子齿形曲线的误差。因此，实际上转子和定子相啮合时的密封腔通常是不会完全密封的，运转时总会有些介质从排出腔泄漏回吸入腔。

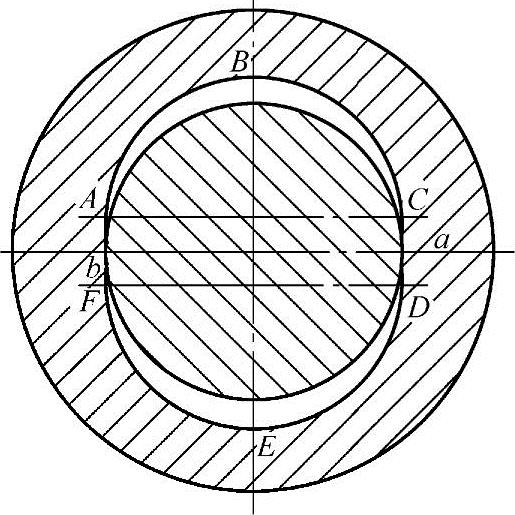
图2-10 转子与定子的端面齿形啮合

以橡胶为材质的定子，在设计时定子和转子之间必须存在微量的过盈，即必须有初始的过盈量，使其有较高的容积效率。因此，实际上两者的啮合已不再是点啮合和线啮合，变成了面接触。从表面看，似乎定子对转子的过盈量大，密封腔的密封程度就会好，但是过盈量大会增加摩擦力，使摩擦损失增大，特别在起动时还会使起动力矩大大增加，造成难以起动的后果。而且过盈量过大会使定子很快磨损。其实，对转子和定子而言，最为重要的是确保加工后齿形曲线的正确，而不是用增大过盈来弥补齿形曲线的误差。

若检查转子和定子的配合密封性好坏，在转子和定子的配合好后可截取一个导程长度，再在孔内灌水。根据泄漏的情况，可看出密封性的好坏，也即可得出加工定子和转子的精度如何的结论。若在转子表面涂以红丹后，装入定子孔内，用手转动转子，再取出，这样从转子的表面也可以看出转子和定子的接触好坏。

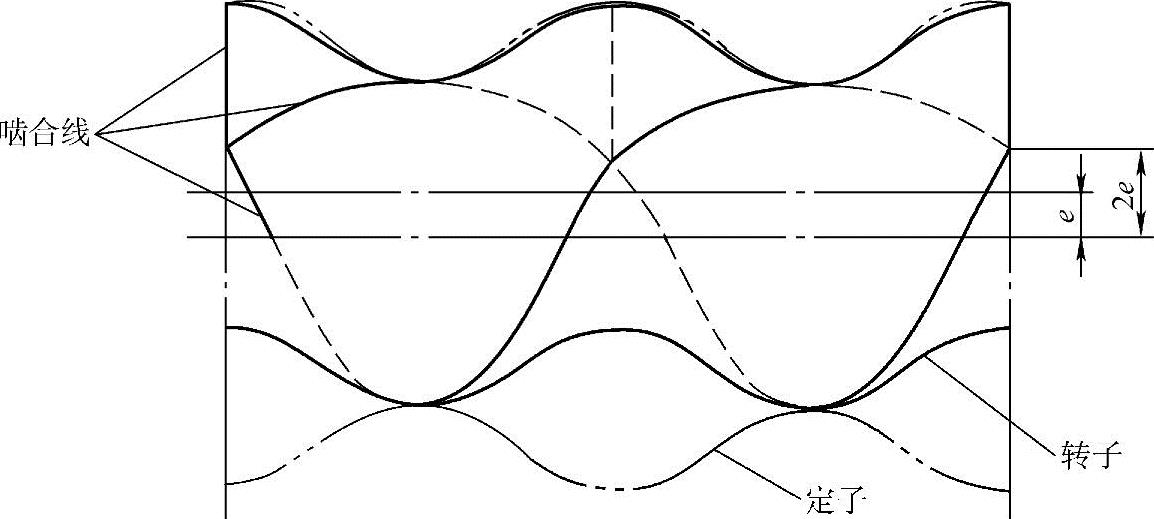
图2-11 理论密封腔