(1)螺旋面的构成 转子的螺旋面其横截面均为半径为R的圆,转子的螺旋型面是其横截面的圆心O1以偏心距e绕转子中心线O2作匀速旋转,并以导程(因是单头螺旋,故此处导程T即为螺距t)匀速向前移动,从而形成左旋或右旋的螺旋型面(图2-1)。
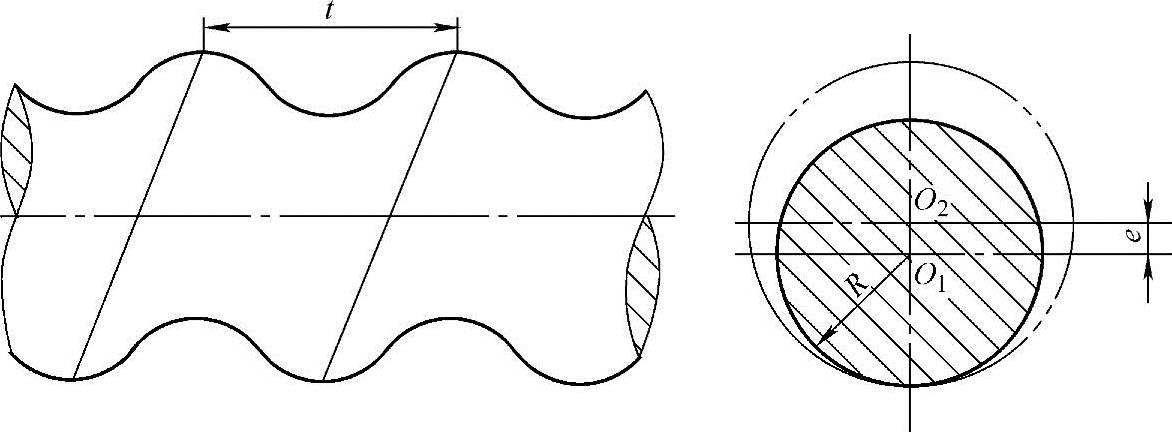
图2-1 转子的形成
单螺杆泵运行时和其他类型的泵最大的不同是:当动力源驱动时,其转子在定子内的运动可看做是行星运动,即偏心为e的转子既绕自身的轴线转动(为相对运动),又因转子中心线对定子的中心线位移为e,又绕定子轴线转动(为绝对运动)。
定子的螺旋面的横截面是由半径与转子半径R相同的两个半圆弧 和
和 以及由上述这两个半圆的圆心之间的距离为4e、宽为2R的长方形ACDF构成(图2-
以及由上述这两个半圆的圆心之间的距离为4e、宽为2R的长方形ACDF构成(图2-
2)。螺旋面是由ABCDEFA曲面一边绕其轴线O作匀速旋转,一边又以T=2t的导程作匀速向前移动,形成左旋或右旋的型面。
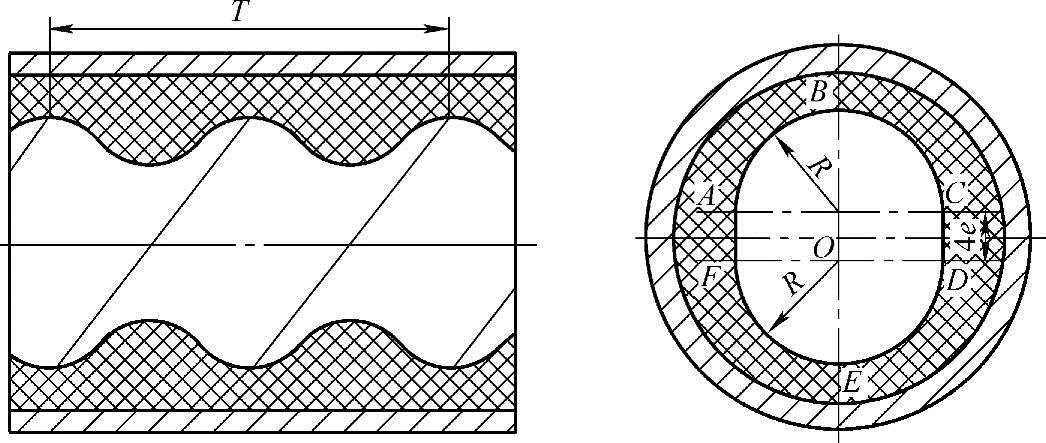
图2-2 定子的形成
显然,转子为单头凸螺旋、定子为双头凹的内螺旋曲面体。转子和定子的螺旋旋向则相同。
(2)转子的齿形曲线方程式 图2-3中转子的横截面是圆心O1、半径为R的圆,O1X1Y1Z1为动坐标系;圆心O2为转子的中心,O1O2为偏心距e,O2XYZ为定坐标系。O1Z轴和O2Z轴垂直纸面(未表示出来)。
显见,转子横截面上任意点M(X1Y1)的方程式为
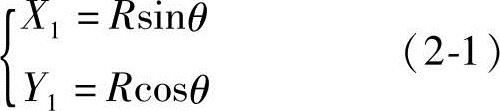
式中 θ——MO1与Y1轴的夹角。
而O1(X01、Y01、Z01)点在定坐标系O2XYZ中的方程式为
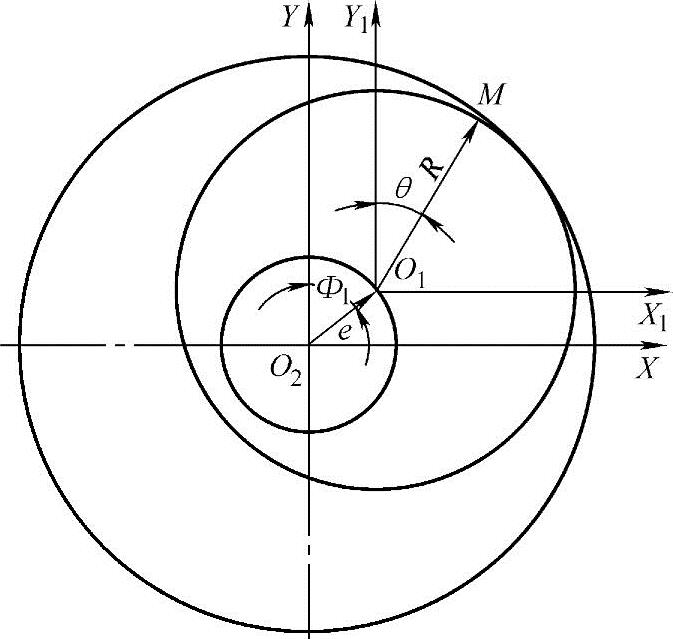
图2-3 转子横截面坐标系

式中 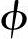 1——O1O2与Y轴的夹角。
1——O1O2与Y轴的夹角。
所以,转子的齿形曲线在坐标系O2XYZ中的方程式为

转子的轴截面用YOZ坐标表示,即X=0,则可得
Rsinθ+esinΦ1=0
即 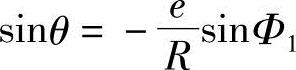
所以 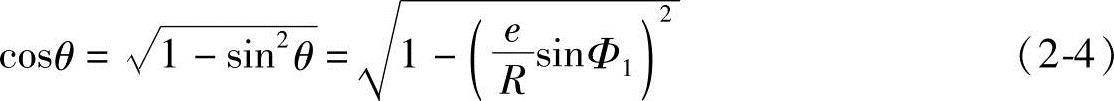
将式(2-4)的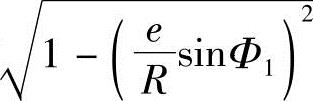 用牛顿二项式展开成级数,略去
用牛顿二项式展开成级数,略去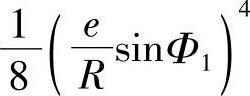 和以后的各项代入式(2-3),就可得转子轴截面方程式
和以后的各项代入式(2-3),就可得转子轴截面方程式
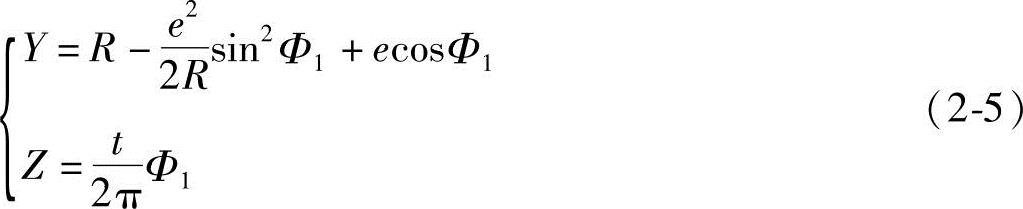
曲线Y=f(Φ1)与转子中心线的距离(即Y)就是轴截面上转子表面的曲线。
(3)定子的齿形曲线方程式 由图2-4可知,在动坐标系OX1Y1Z1中,定子齿形曲线的 段上任意点M(X1、Y1)的方程式为
段上任意点M(X1、Y1)的方程式为
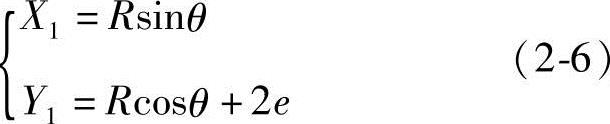
式中 θ——MO1与Y1轴的夹角
当动坐标系OX1Y1绕定子轴心线O即图2-4未表示出来的Z轴(垂直纸面)转动θ0时,得方程式为
 (https://www.xing528.com)
(https://www.xing528.com)
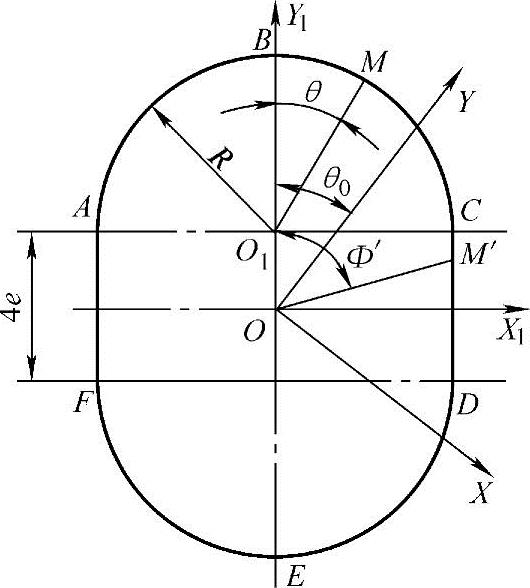
图2-4 定子横截面的坐标系
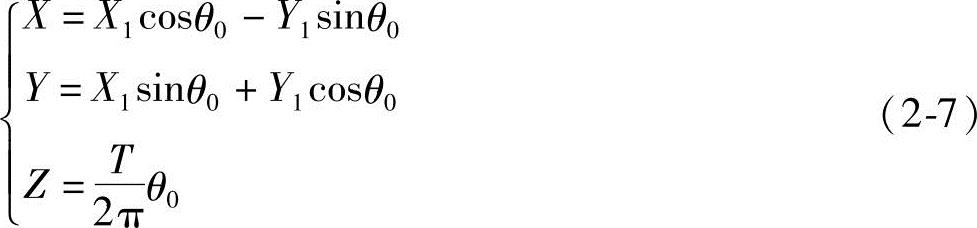
将式(2-6)代入式(2-7),可得定子齿形曲线方程式
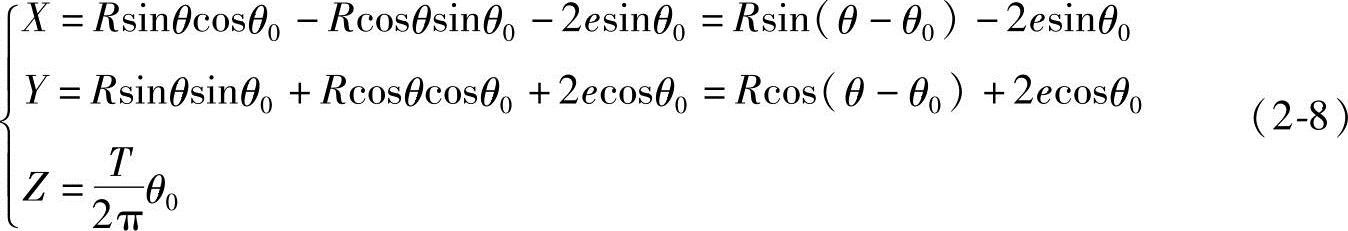
式中 -π/2≤θ≤π/2;0≤θ0≤2πn,其中n为整数。
图2-4中齿形曲线的直线段CD和AF上的任意点M′有

将式(2-9)代入式(2-7)可得
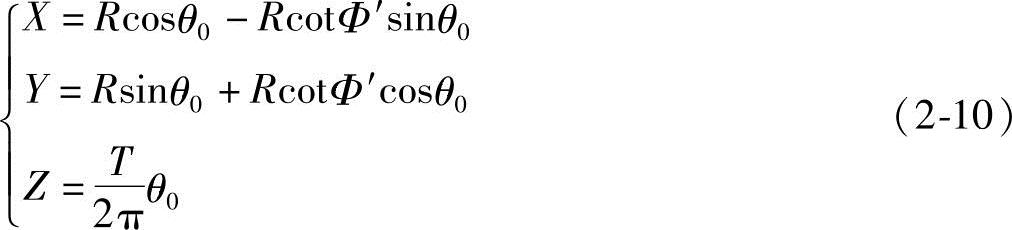
式中 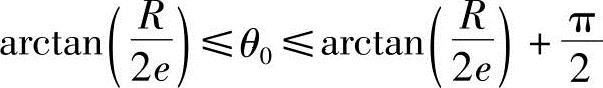 ;0≤θ0≤2πn,其中n为整数。
;0≤θ0≤2πn,其中n为整数。
所以,定子的轴截面方程式,即当X=0时,YOZ平面上的曲线方程。
对A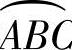 C段,由式(2-8)得Rsin(θ-θ0)-2esinθ0=0
C段,由式(2-8)得Rsin(θ-θ0)-2esinθ0=0
即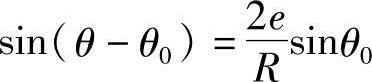
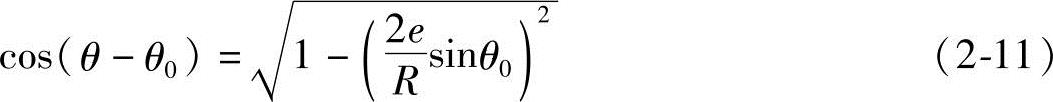
将式(2-11)代入式(2-8),可得
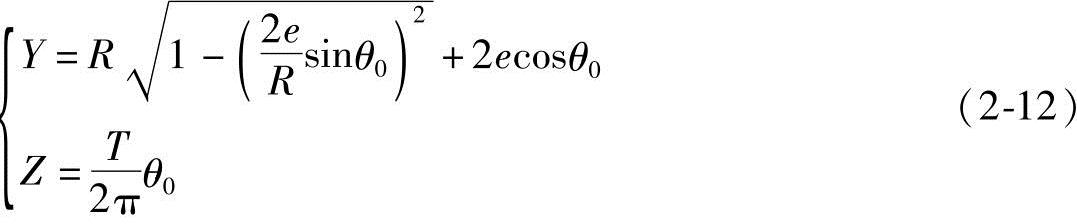
将式(2-12)中的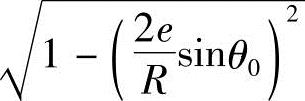 用牛顿二项式展开成级数,略去级数
用牛顿二项式展开成级数,略去级数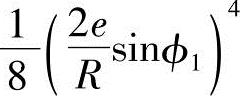 以后的各项,即可得用于计算定子轴截面齿形样板用的较为精确的方程式
以后的各项,即可得用于计算定子轴截面齿形样板用的较为精确的方程式
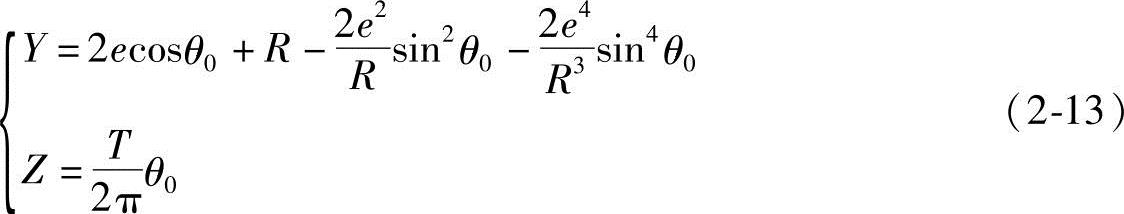
对CD和AF段直线,由式(2-10)得
Rcosθ0-RcotΦ′sinθ0=0
即 
将式(2-14)代入式(2-10),可得
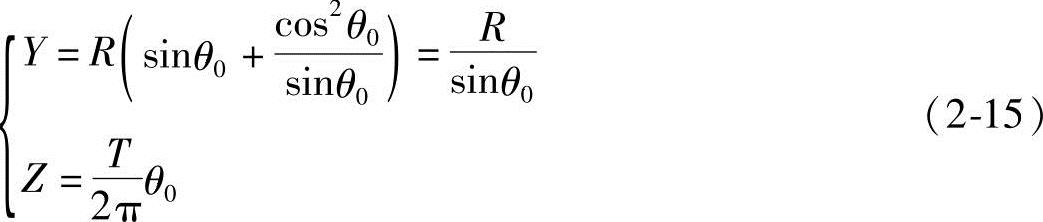
由式(2-13)和式(2-15)就可以绘出定子的轴截面齿形。
通常式(2-12)式中的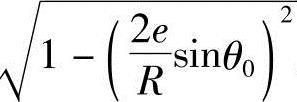 用牛顿二项式展开,略去级数
用牛顿二项式展开,略去级数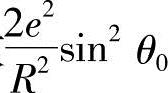 以后的各项,即可应用。故定子轴截面的简化方程式为
以后的各项,即可应用。故定子轴截面的简化方程式为
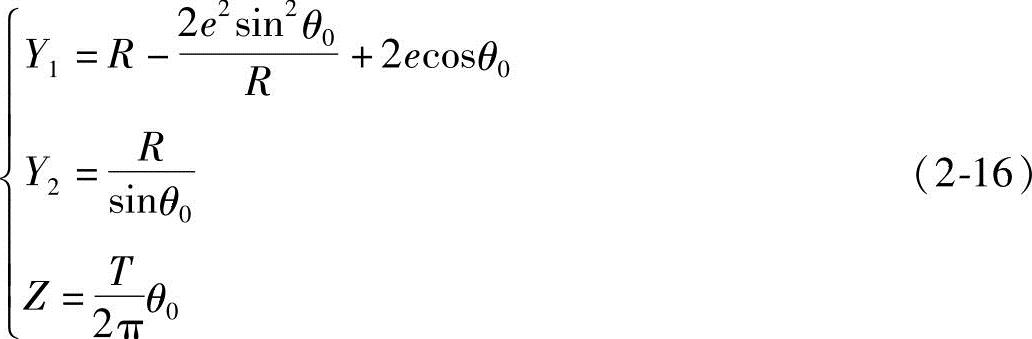
式(2-16)中Y1为定子齿形曲线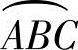 和
和 段上的任意点M的坐标值,M点在不同的位置。式(2-6)中的正负号应作相应改变;式(2-16)中Y2为定子齿形曲线CD和AF直线段上的任意点M′的坐标值,M′点在不同的位置,式(2-9)式中正负号也应作相应改变。
段上的任意点M的坐标值,M点在不同的位置。式(2-6)中的正负号应作相应改变;式(2-16)中Y2为定子齿形曲线CD和AF直线段上的任意点M′的坐标值,M′点在不同的位置,式(2-9)式中正负号也应作相应改变。
由于T=2t,由式(2-5)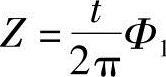 和式(2-16)
和式(2-16)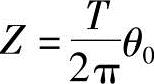 ,可知
,可知
Φ1=2θ0 (2-17)
将式(2-17)代入式(2-5)中,转子轴截面方程式也可表示为
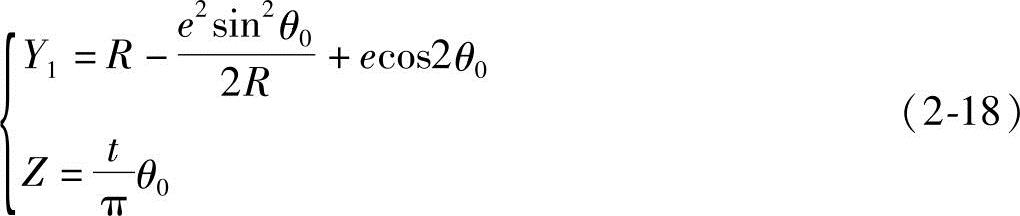
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




