摆线啮合线及其应用分析

（1）外摆线的啮合线 若外摆线和其共轭齿形曲线的相切之点移动，即为第五节坐标系旋转中提到的坐标系旋转了θ₁角，将动坐标系X₁′O₁Y₁′转换到固定坐标系X₁O₁Y₁。在这种情况下，共轭齿形曲线切点的移动轨迹（也就是啮合线）在固定坐标系X₁O₁Y₁中的方程式为式（1-64）。

将外摆线方程式（1-10）代入式（1-64），则可得外摆线啮合线上任意点M的方程式

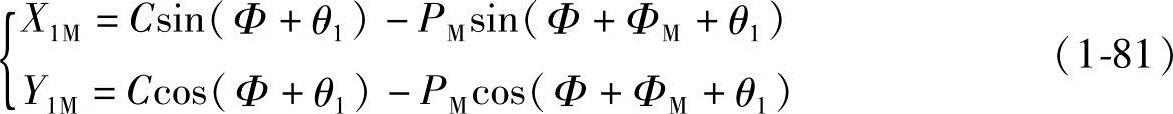
将式（1-71）θ₁=-Φ代入式（1-81），可得

将固定坐标系X₁O₁Y₁平移到发生圆的圆心O₂为原点的坐标系，即坐标系平移了（R+R₁）（图1-11）此时式（1-82）变化为

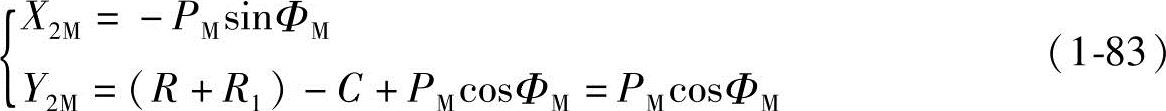
由式（1-83）可以看出，外摆线的啮合线（即共轭齿形曲线切点的移动轨迹）为：以发生圆圆心O₂为圆心、摆点M的半径P_M为半径的圆弧。从图1-2可知，外摆线齿形曲线位于Y轴的右边，现式（1-83）中X_2M为负值，即表示齿形曲线切点位于Y轴左边。故啮合线与外摆线齿形曲线分别在Y轴的两边。这一结论对分析螺杆泵螺杆螺旋型面啮合线具有十分重要的意义。外摆线齿形曲线的啮合线与短幅外摆线齿形曲线的啮合线情况相同，在此不再赘述（图1-11和图1-12）

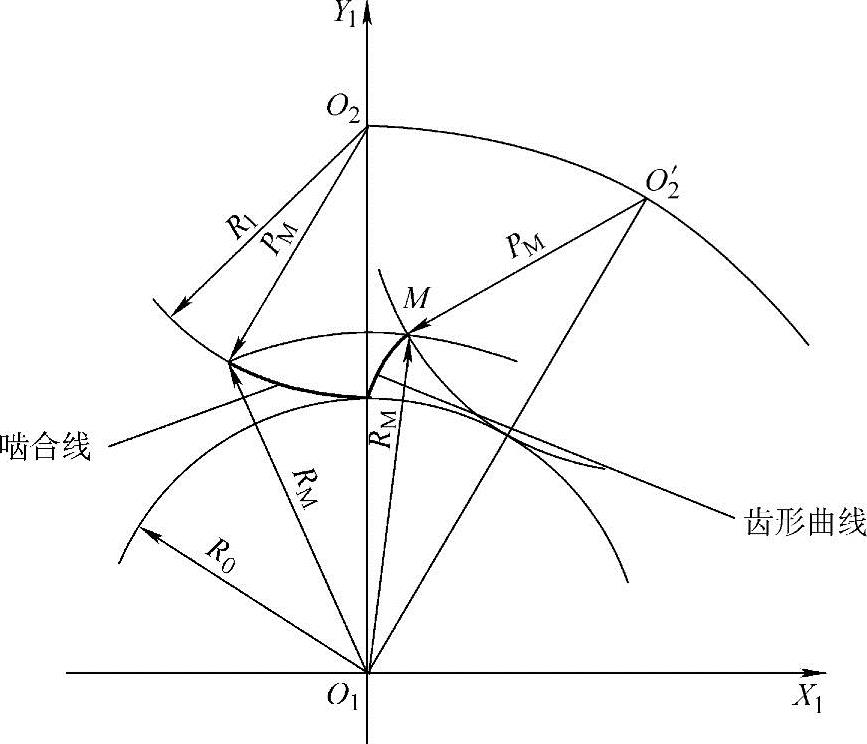
图1-11 外摆线的啮合线(www.xing528.com)

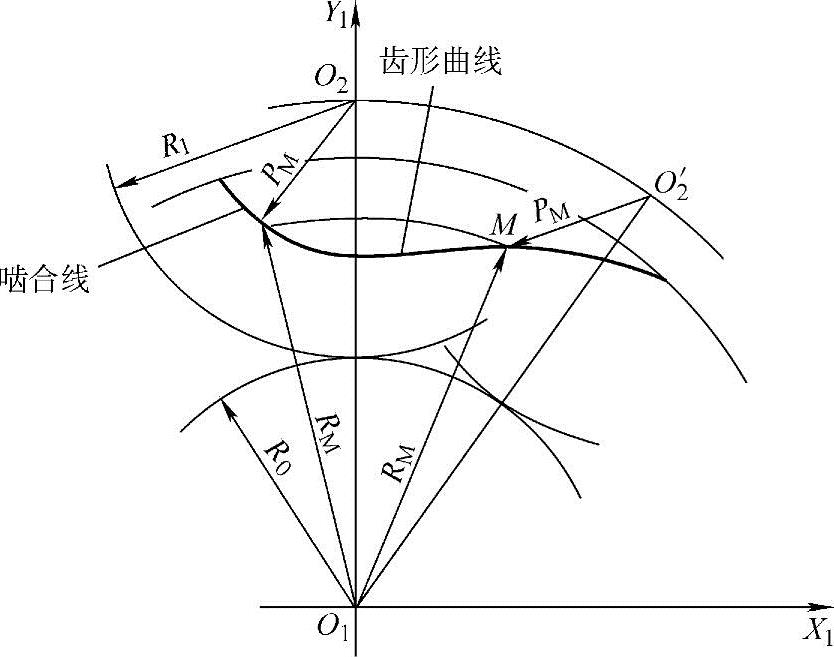
图1-12 短幅外摆线的啮合线

（2）长幅外摆线的啮合线 同上述外摆线的啮合线推导相仿，将长幅外摆线方程式（1-17）代入式（1-64），则可得长幅外摆线啮合线上任意点M的方程式：

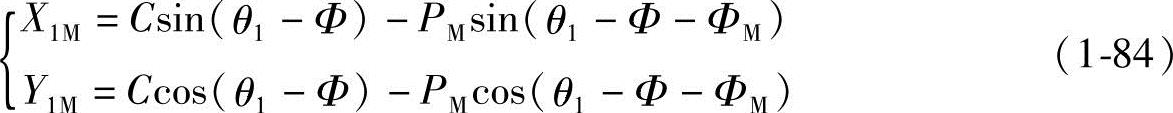
将式（1-75）θ₁=-Φ代入式（1-84），可得

将固定坐标系X₁O₁Y₁平移到发生圆的圆心O₂为原点的坐标系，即坐标系平移了（R+R₁）（图1-13），此时式（1-85）变化为

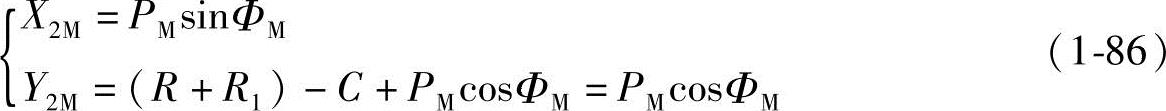
由式（1-86）可以看出，长幅外摆线的啮合线，即共轭齿形曲线切点的移动轨迹为：以发生圆的圆心O₂为圆心、摆点M的半径P_M为半径的圆弧。而从图1-3可知，长幅外摆线齿形曲线位于Y轴的右边，现式（1-84）中X_2M为正值，即表示齿形曲线切点也位于Y轴的右边。故与长幅外摆线的齿形曲线同在Y轴的一边（图1-13）。这是与外摆线和短幅外摆线的啮合线不相同的地方。