螺杆齿形共轭曲线详解

（1）外摆线和短幅外摆线的共轭曲线 由第四节已知外摆线方程式（1-10）和短幅外摆线方程式（1-24）；图1-2和图1-4中的C=R+R₁。由于R为定圆半径，也可将其看作螺杆螺旋的节圆，故R=r_j1，Φ_M即为齿形转角。所以外摆线和短幅外摆线的方程式可以统一表示为

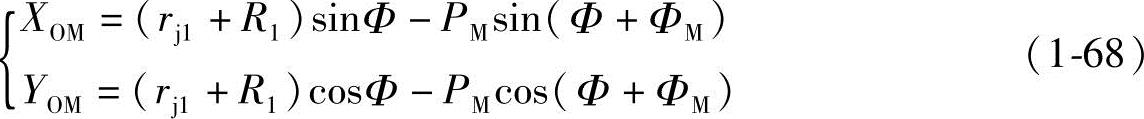
也就是说，可以将式（1-68）中的X_OM和Y_OM看作式（1-66）中的X₁′和Y₁′。现将式（1-68）代入式（1-66），可得

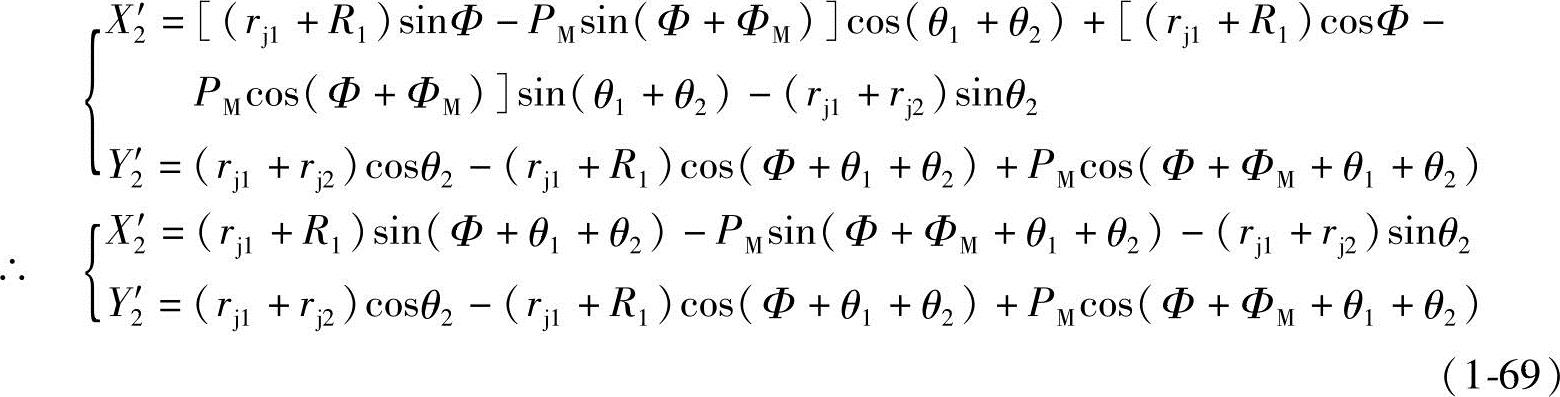
从式（1-69）可知，X′₂和Y′₂有Φ、Φ_M、θ₁和θ₂四个参变数，由动圆转角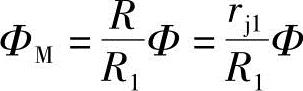和式（1-67）可知，这四个参变数实际上只是两个参变数。而齿型共轭的两曲线的切点是随着螺杆的转角θ₁而变动，故齿形曲线切点的齿形参数Φ与转角θ₁的关系可由如下条件来确定：

将式（1-67）和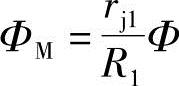代入式（1-69），

因为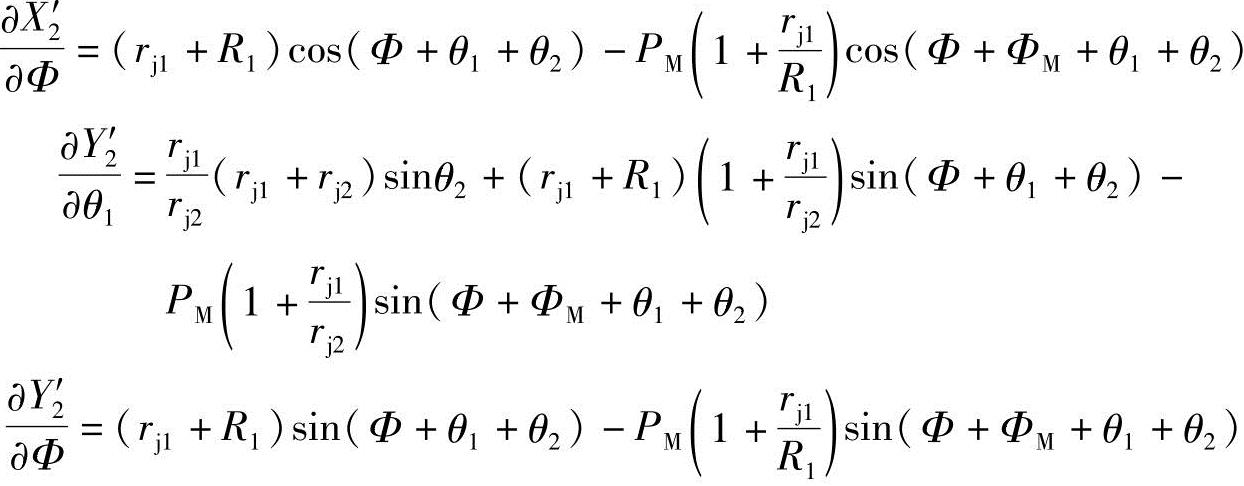

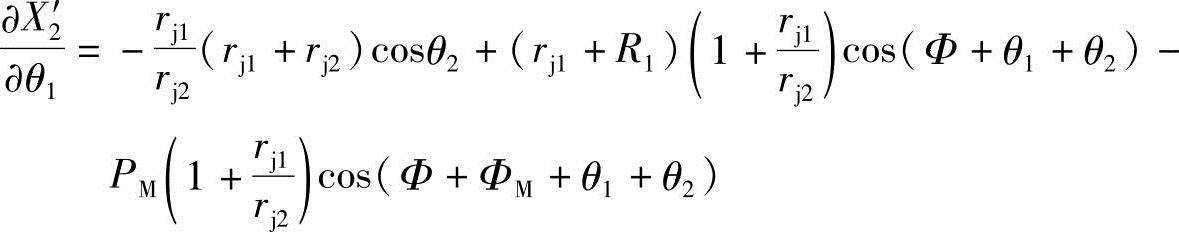
所以，将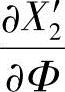、、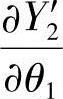、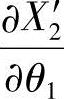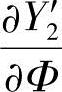代入式（1-70）后，整理可得

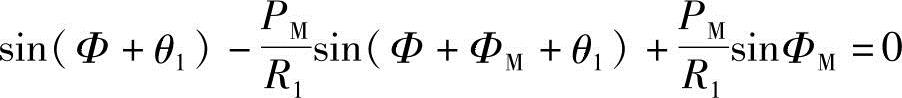
即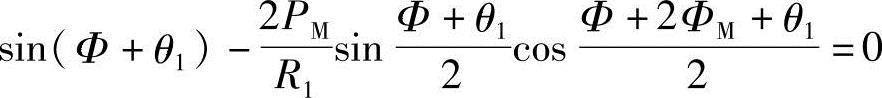

所以，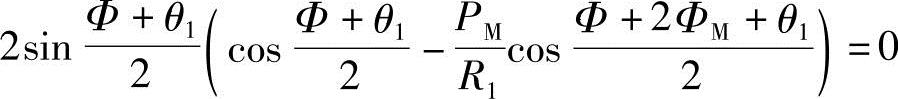

由此可得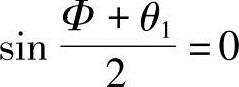，即Φ+θ₁=0

所以，θ₁=-Φ

由式（1-67）得：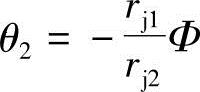

对于两根螺杆而言，存在着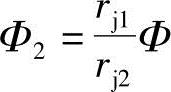的关系式

所以，θ₂=-Φ （1-71）

将上述四个参变数之间的关系式代入式（1-69），可得

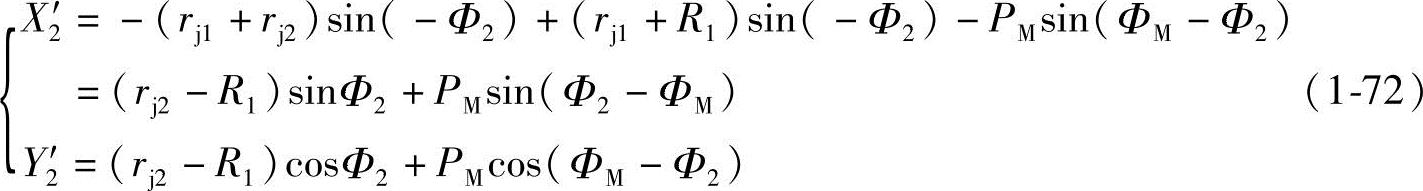
由上可知，外摆线和短幅外摆线的共轭齿形曲线方程式（1-72）和内摆线方程式（1-32）形式相同，差别仅仅由于转动方向不同造成的。可见，外摆线的共轭齿形曲线为内摆线，反之内摆线的共轭齿形曲线为外摆线。

可以推出：两根螺杆为共轭齿形曲线，则必是由同一发生圆、同一摆点半径P_M所形成，而且发生圆必定与螺杆螺旋的节圆相切。若发生圆位于一根螺杆螺旋的节圆之外（形成的齿形曲线为外摆线），则这一发生圆也必定位于另一根螺杆螺旋的节圆之内，形成的齿形曲线为内摆线。

对某些螺杆泵而言，发生圆即为另一螺杆螺旋的节圆，即R₁=r_j2，且发生圆与另一螺杆螺旋节圆的圆心相同，即Φ_M=Φ₂。此种情况下，从式（1-72）可以看出，外摆线的共轭曲线已不再是曲线，而变成了一个点，即点成为共轭齿形曲线内摆线的特殊情况。在此种情况下，X₂′=0，Y₂′=P_M，即点M距离另一螺杆圆心O₂为P_M。

（2）长幅外摆线的共轭曲线 与求外摆线的共轭曲线相仿：将X_OM和Y_OM看做式（1-17）中的X₁′和Y₁′，C=r_j1+R₁。

将长幅外摆线的方程式（1-17）代入式（1-66），得(www.xing528.com)

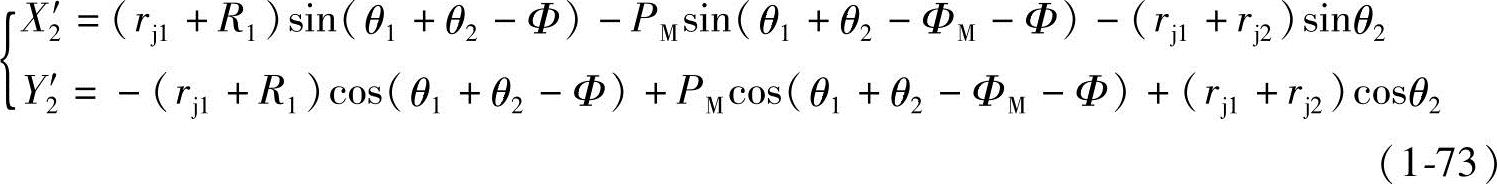
为确定Φ、Φ_M、θ₁和θ₂四个参变数之间的关系，求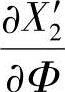、、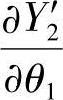、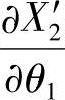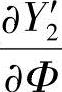，并将得到的结果代入式（1-70），进行整理后可得

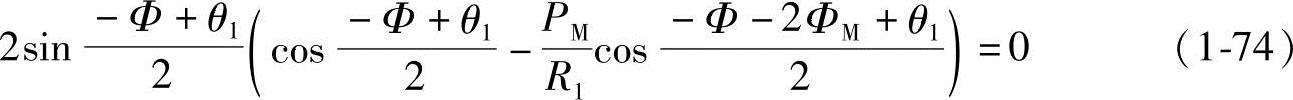
所以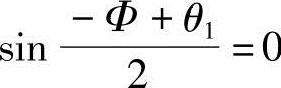，，即-Φ+θ₁=0，θ₁=Φ

由式（1-67）得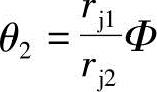

对于两根螺杆而言，存在着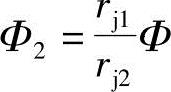的关系式：

θ₂=Φ₂ （1-75）

将所得的上述四个参变数之间的关系式代入式（1-73），可得

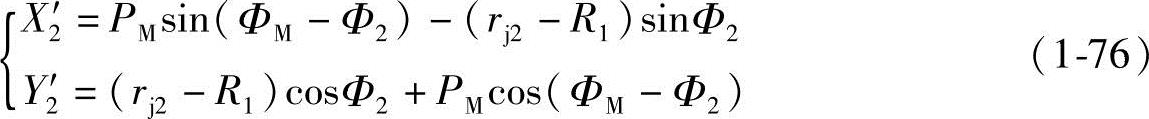
由上可知，长幅外摆线的共轭齿形曲线方程式（1-76）和内摆线方程式（1-32）形式完全相同。即其共轭齿形曲线为内摆线。

也可以推出：两根螺杆为共轭齿形曲线，则必是同一发生圆和同一摆点半径P_M所形成。

对某些螺杆泵而言，发生圆即为另一螺杆螺旋的节圆，即R₁=r_j2，且Φ_M=Φ₂，此种情况下，式（1-76）变为：X₂′=0，Y₂′=P_M，即长幅外摆线的共轭曲线变为一个点，这就成了其共轭曲线为内摆线的一种特殊情况。此时，点M距离另一螺杆圆心O₂为P_M。

（3）渐开线的共轭曲线 若考虑渐开线的坐标系转了θ₀角，则将渐开线的方程式（1-50）代入式（1-66），螺杆1上的渐开线在螺杆2上的共轭曲线方程式为

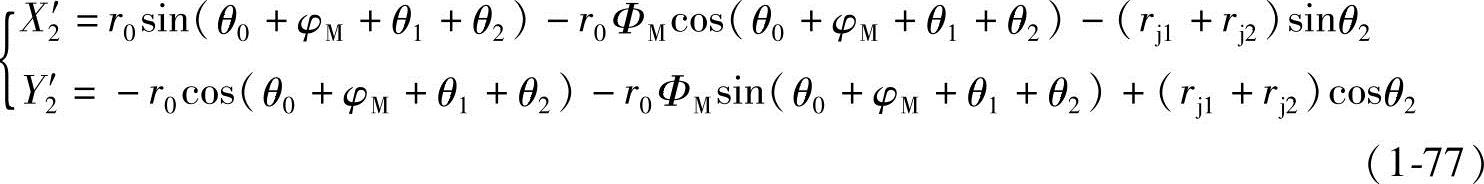
与求外摆线共轭曲线相仿，其参变数之间关系由式（1-70）得。将求得的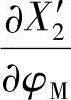、、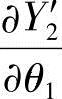、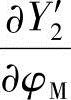，代入式（1-70），并整理后可得出：

对螺杆而言，

式中 α——啮合角。

将式（1-79）代入式（1-78）得cos（θ₁+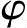_M）=cosα；

θ₁+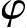_M=α （1-80）

再把式（1-80）代入式（1-76），经整理可得出的X₂′和Y₂′的方程式，即为渐开

线方程式的形式。由于渐开线的共轭曲线必为渐开线，而对其的求证和推导又较复杂，在此就不

作详细介绍。