齿形曲线的等距线及其法线方向距离

螺杆泵螺杆螺旋面加工时，需要计算刀具的齿形曲线坐标值，此坐标值为螺旋面某一截面理论上的坐标值。实际上螺杆在运行时，相啮合的螺杆螺旋面之间必须存在一定的啮合间隙，才可能进行正常的运行。因此，须对刀具的理论齿形曲线的坐标值进行修正，这种修正方式邓定国和朱鹏程采用等距线的修正。若刀具理论齿形曲线为mm，它是由一系列离散的坐标点组成的（图1-9）。所谓齿形曲线mm的等距线m′m′，即距mm上的每一点的法线方向距离均为δ的点的集合。

若在mm上任意点M的法线矢量n上取MM′=δ，则M′就是距齿形曲线mm为δ的等距线m′m′上的一个点。

设OM（X，Y）=r

OM′（X′，Y′）=r′

所以r′=r+MM′

MM′=|MM′|e=δ·e

式中 e——mm齿形曲线上M点的单位法向矢量，其矢量坐标为

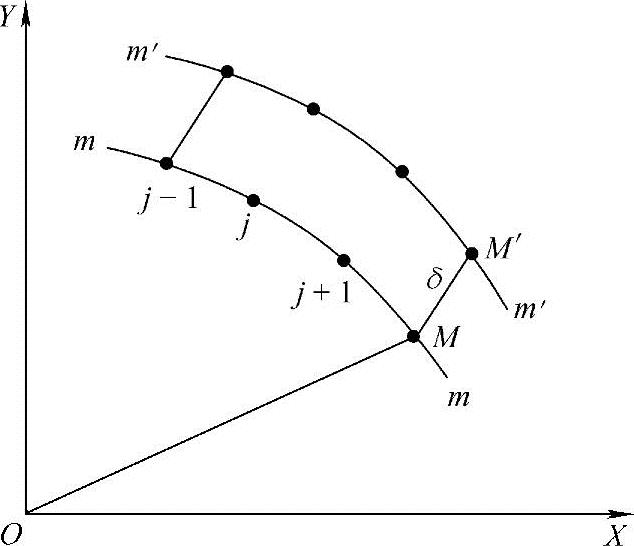
图1-9 齿形曲线的等距线

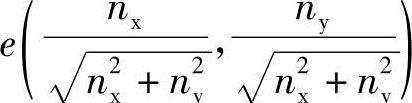
故等距线m′m′的方程为r′=r+δ·e

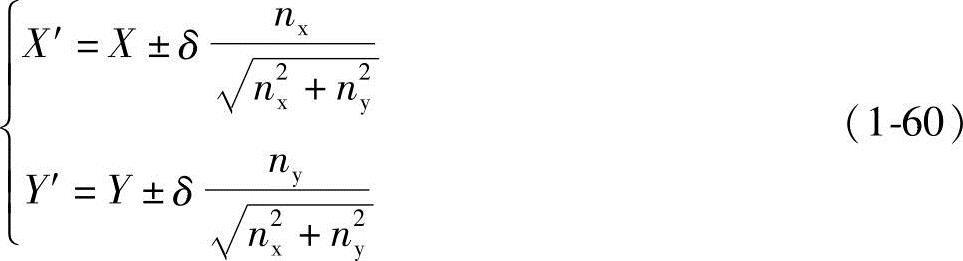(www.xing528.com)

式中的正负号是指齿形曲线mm的上或下两条等距线。

若以曲线的切线斜率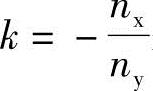表示，则式（1-59）可写成

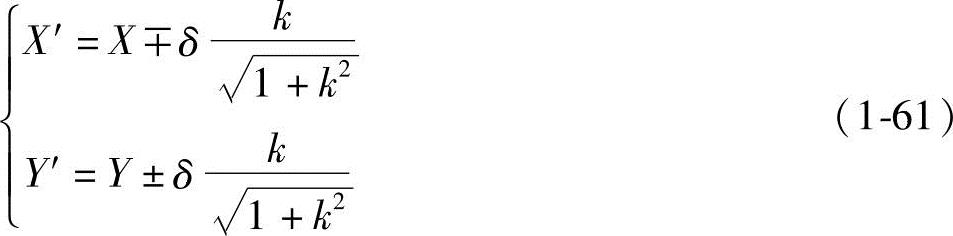
由于齿形曲线mm是由一系列离散的坐标点形成的，故上述的法向矢量n_x、n_y或切线斜率k只能用数值微分法近似表示。

现齿形曲线mm上的三个点，j_-1（X_j-1，Y_j-1）、j（X_j，Y_j）和j₊₁（X_j+1，Y_j+1）用拉格朗日插值多项式L（X）近似表示通过这三个点的曲线方程

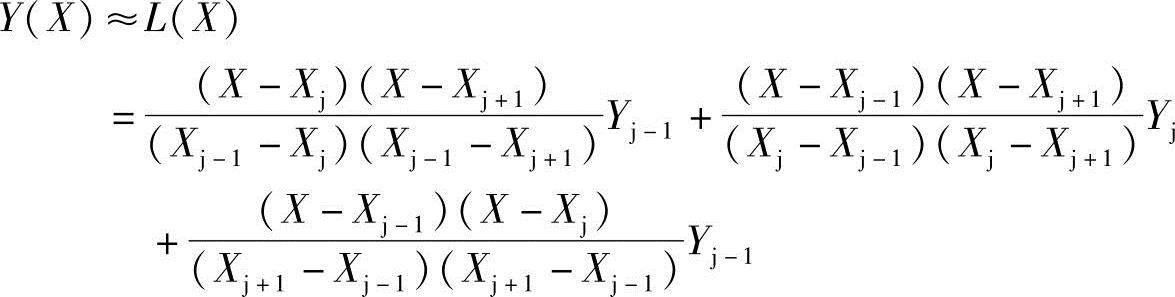
对上式求理论齿形曲线mm的一阶导数，即切线斜率k

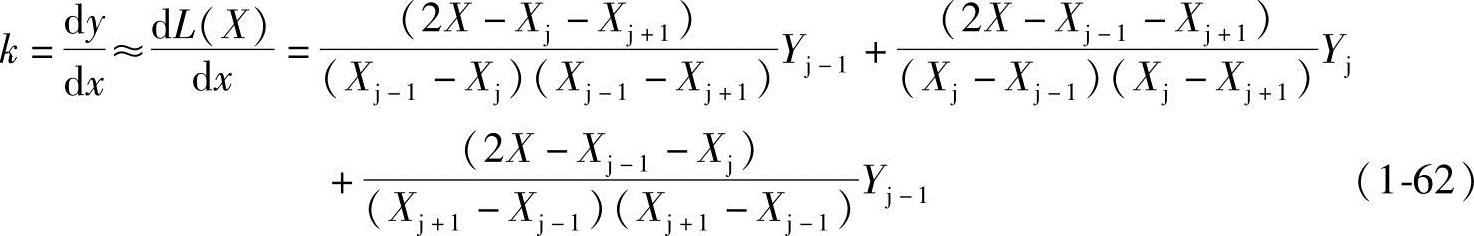
求第j点的一阶导数k，只要令式（1-62）中X=X_j即可得

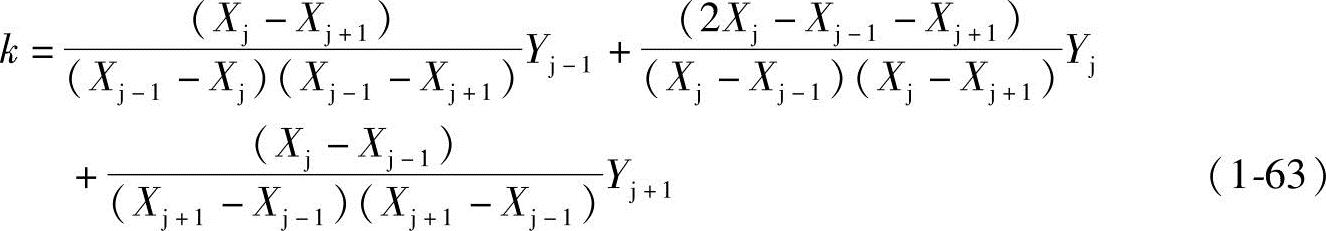
逐点求出一阶导数k后，代入式（1-61），就得到mm的近似等距线m′m′。