螺旋端面的渐开线齿形曲线分析

（1）渐开线齿形曲线 假如形成摆线的动圆，即发生圆的半径趋向无穷大时，此种情况下，动圆就变成了一条直线，当这条直线在定圆上滚动时，直线上一点的轨迹就是定圆的渐开线。所以可以把渐开线看作摆线的特殊情况。

图1-6中发生线KL沿着半径r₀的基圆圆周作纯滚动时，发生线上M点的轨迹曲线MN即为渐开线。

可见渐开线齿形上的任意点M到基圆的切线之长MK等于切点K到曲线起点M运动至基圆圆弧上的点N的弧长。

基圆半径为r₀的渐开线上任意点M的直角坐标参数方程式由图1-6可知：

图1-6 渐开线

式中 θ——渐开线极角，为渐开线上某点（如：M点）的向量半径R_M与通过渐开线起点N的Y₀轴之间的夹角。

θ=_M-α （1-45）

式中 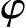_M——渐开线上任意点M的基圆展开角，为渐开线上任意点M与基圆相切之点K和通过渐开线起点N的Y₀轴之间的夹角。

α——渐开线啮合角，由图1-6可得α=arctan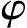_M。

由图1-6中的△OMK可知，M点的向量半径R_M和啮合角α为

(www.xing528.com)

即

将式（1-46）和式（1-47）代入式（1-45）可得极角θ方程式：

所以，渐开线的极坐标参数方程式则为

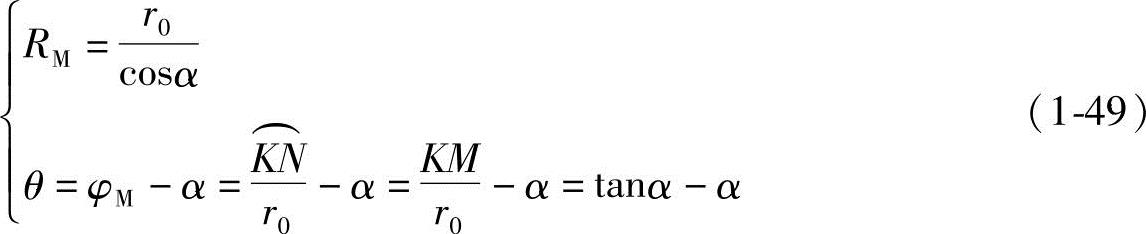
（2）坐标系旋转 渐开线所在的坐标系转了θ₀角后，其直角坐标参数方程式（1-44）变为

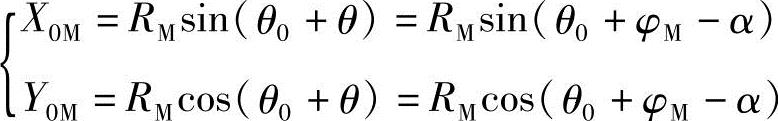
即：

由图1-6可知：R_Mcosα=r₀，R_Msinα=r_0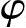M，