(1)外摆线齿形曲线 图1-2中半径为R1的动圆O1沿半径为R的定圆O的外圆作纯滚动(即无滑动的滚动)时,动圆O1上的一点N的运动轨迹NM称为外摆线。N点称为摆点,也称描绘点;动圆也称为发生圆。
为了简化后面的方程式,将Y0轴设置在通过曲线的起点。
由图1-2可知,外摆线上任意点M的坐标值为
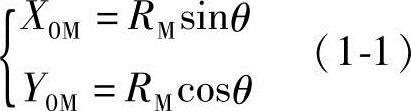
式中 θ——定圆圆心O至M点的半径和Y0轴之间的夹角,称为齿形极角。
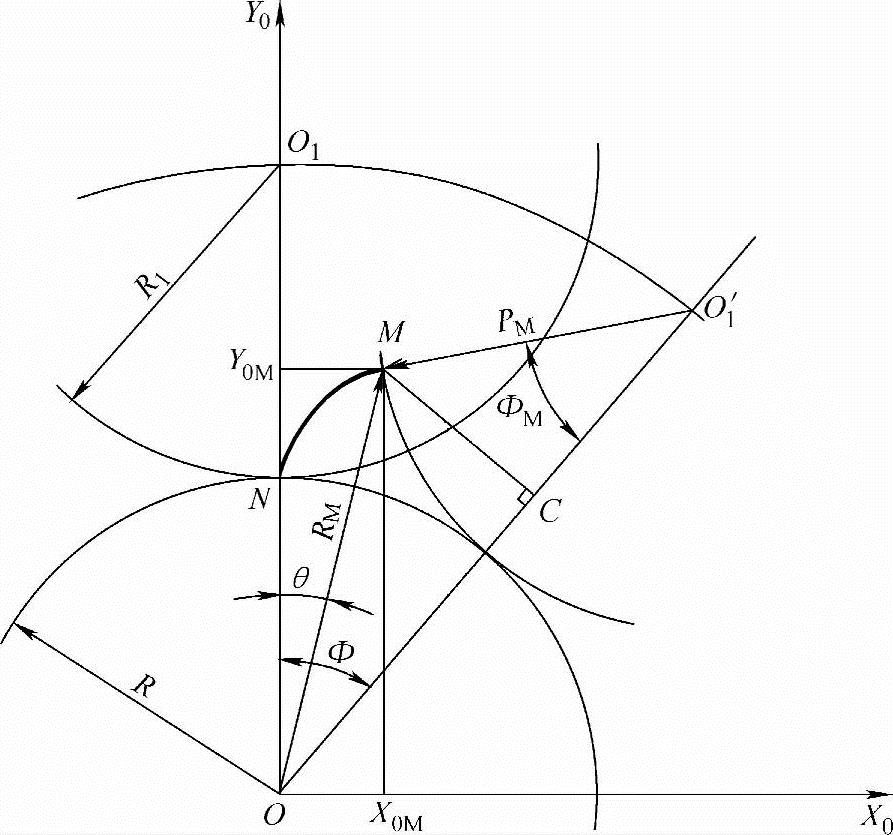
图1-2 外摆线
若Y0轴不通过曲线的起点,而与曲线的起点成θ0角时,则有关公式的变化将在本节坐标系旋转中讲述。
由图1-2可知,对于外摆线上任意点M,O1′M=R1。为了与后面叙述的长幅外摆线和短幅外摆线表达一致,此处将O1′M表示为PM。动圆O1转了ΦM角,定圆O相应地也转了角Φ,由于两圆作纯滚动,其滚动的圆弧也相等,由此可得

因为Φ=iΦM
θ=θ+Φ-Φ=iΦM-(Φ-θ) (1-3)
由图1-2中的△OMO1′可得
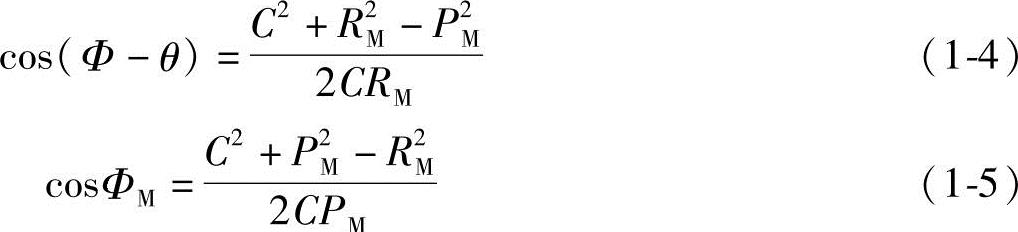
式中 ΦM——动圆转角,称为螺杆的齿形转角;
RM——定圆圆心O至外摆线上任意点M之间的距离;
C——定圆O与动圆O1两圆心之间的距离为O1′O,C=R+R1。
所以,将式(1-4)和式(1-5)代入式(1-3),可得外摆线的极坐标方程式:
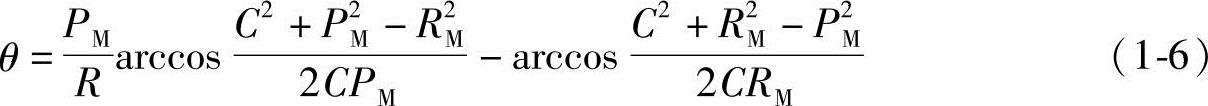
可见,只需要知道M点的半径RM,即摆点N摆至M点的半径和动圆的半径R1,就可以求得θ,从而由式(1-1)可得M点的坐标值X0M和Y0M。
从式(1-1)也可推导得到M点的直角坐标方程式:
X0M=RMsin(Φ-Φ+θ)=RMsinΦcos(Φ-θ)-RMcosΦsin(Φ-θ) (1-7)
由△OMO′得
RMsin(Φ-θ)=PMsinΦM (1-8)
RMcos(Φ-θ)=C-PMcosΦM (1-9)
将式(1-8)和式(1-9)代入式(1-7),得
X0M=(C-PMcosΦM)sinΦ-PMsinΦMcosΦ=CsinΦ-PMsin(Φ+ΦM)
同理可得
Y0M=RMcos(Φ-Φ+θ)=CcosΦ-PMcos(Φ+ΦM)
所以,外摆线任意点M的直角坐标方程为
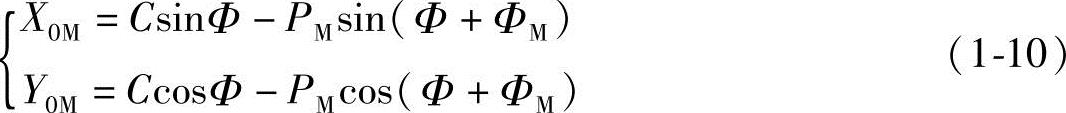
由式(1-2)可知,式(1-10)中的Φ和ΦM,实际上就是一个参数。改变ΦM,可以从式(1-10)得到外摆线的齿形曲线,故ΦM角称之为齿形转角。
所以,极角θ也可由直角坐标得到
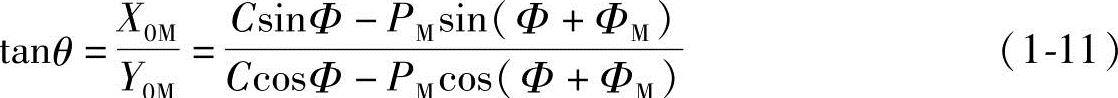
设计螺杆泵时,往往是已选定了齿形曲线及其二端的半径,然后求其角度和坐标值。若已知外摆线齿形曲线的两端半径,则从式(1-5)可求得ΦM,再将ΦM代入式(1-2),即可求得齿形曲线两端的齿形转角Φ。显然,采用极坐标参数方程式(1-1)和式(1-6)来求其角度和坐标值,比用直角坐标参数方程式方便。
上述的外摆线方程式是在动圆O1沿定圆O作顺时针方向滚动时得到的。若动圆沿定圆作逆时针方向滚动,则由图1-2可看出,X0M应为负值,故式(1-10)和式(1-11)中的有关正负号也应作相应的变动。在下面叙述的各种摆线齿形曲线时,情况相似,将不再赘述。
(2)长幅外摆线齿形曲线 当半径R1的动圆O1沿半径为R的定圆O的外圆作纯滚动时,与动圆O1固定的圆外一点N的运动轨迹NM称为长幅外摆线。N点即为摆点。
由图1-3可得

与前面叙述的外摆线相似,可知:
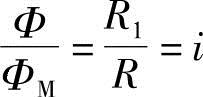
因为Φ=iΦM
θ=θ+Φ-Φ=θ+Φ-iΦM (1-13)
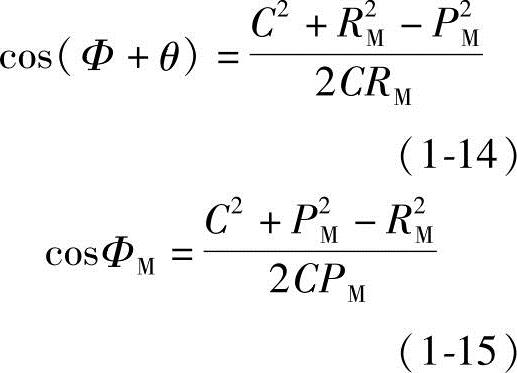
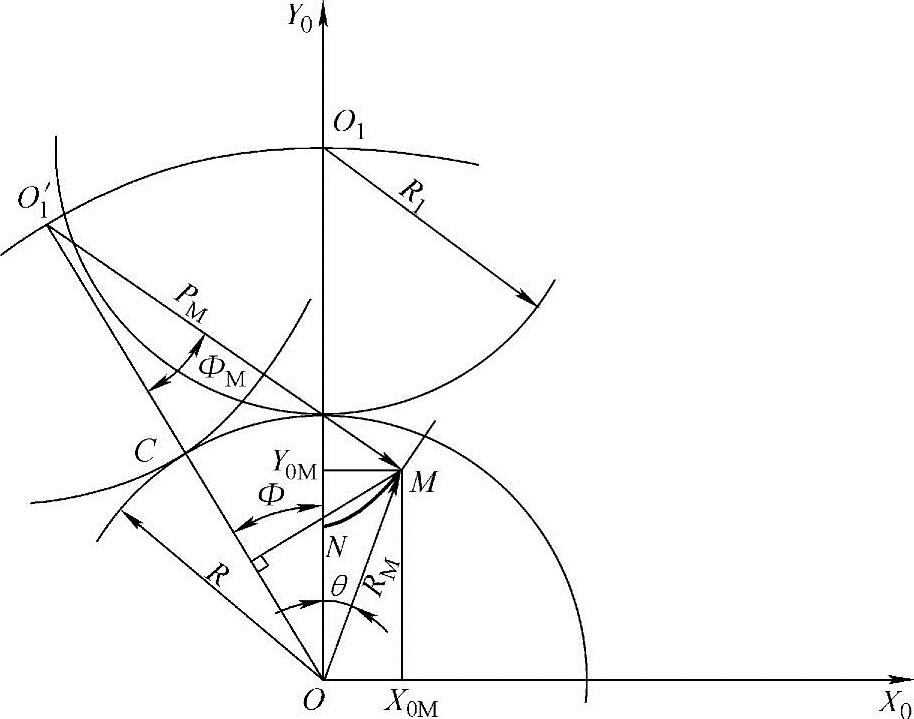
图1-3 长幅外摆线
式中 RM——定圆圆心从O至长幅外摆线上任意点M之间的距离;
PM——动圆圆心O1′至长幅外摆线上任意点M之间的距离;
C——定圆O与动圆O1′两圆心之间的距离为O1′O,C=R+R1。
所以,将式(1-14)和式(1-15)代入式(1-13)可得长幅外摆线的极坐标方程式为
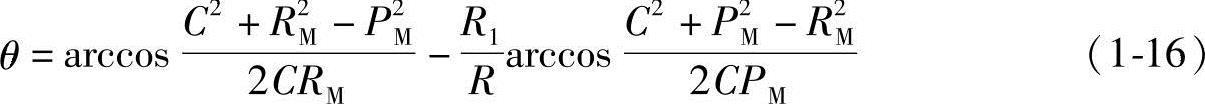
可见,只需要知道摆线N摆至M点的半径RM和摆点半径PM,就可以求得θ角,从而由式(1-12)可得M点的坐标值X0M和Y0M。
与外摆线的推导相仿,从式(1-12)也可推导得出长幅外摆线的齿形任意点M点的直角坐标参数方程式
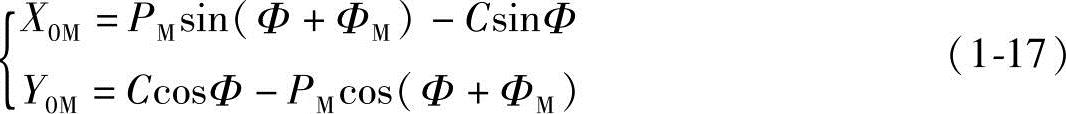
所以,极角θ也可由直角坐标得到
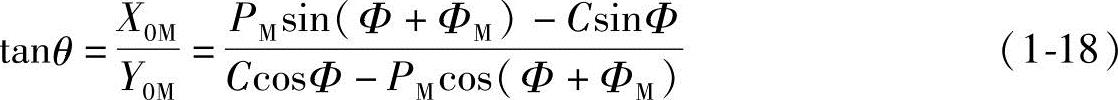
(3)短幅外摆线齿形曲线 当半径R1的动圆O1沿半径为R的定圆O的外圆作纯滚动时,与动圆O1固定的圆内一点N的运动轨迹NM称为短幅外摆线。N点即为摆点。
由图1-4可知,短幅外摆线上任意点M的坐标值为
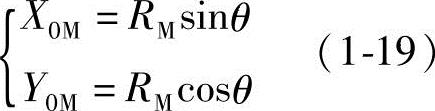
与上述同理,可以推得
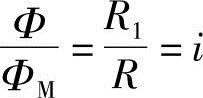
因为Φ=iΦM
θ=θ+Φ-Φ
=iΦM-(Φ-θ) (1-20)(https://www.xing528.com)
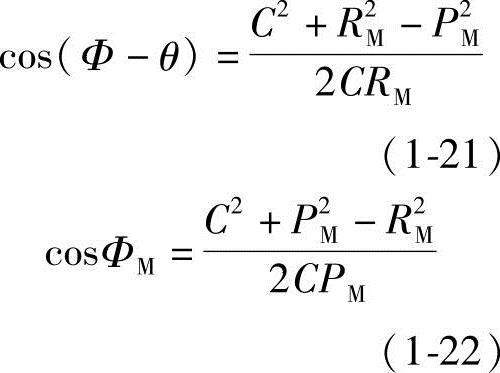
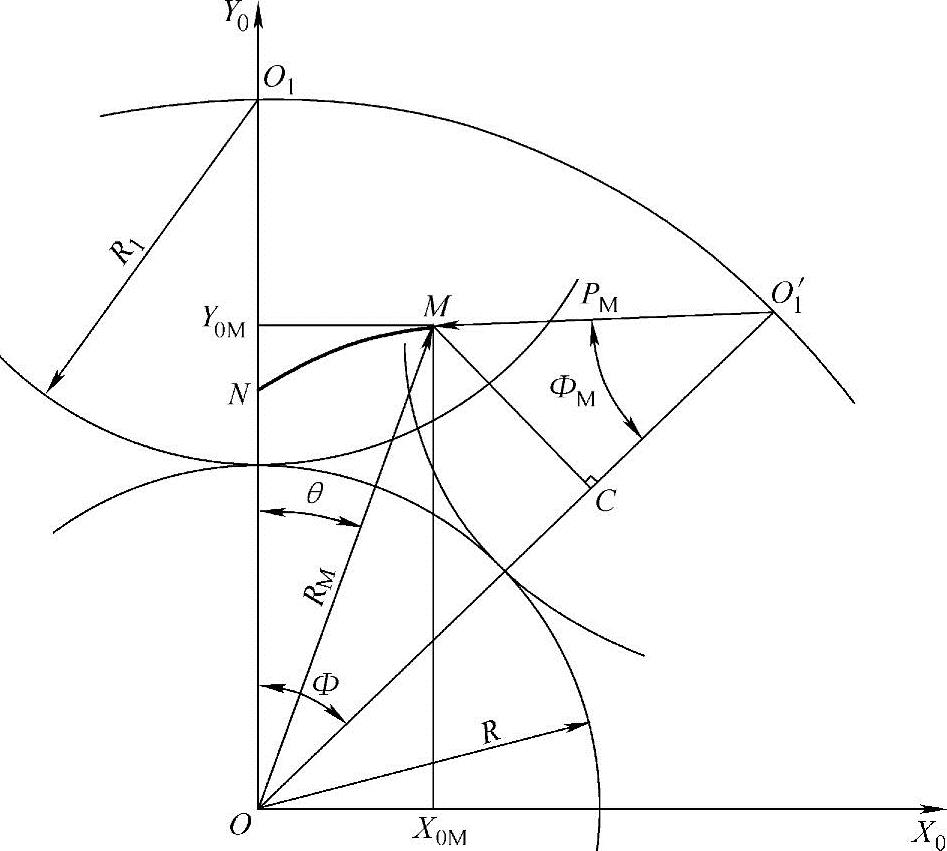
图1-4 短幅外摆线
式中 C——定圆O与动圆O1′两圆心之间的距离为O1′O,C=R+R1;
PM——动圆圆心O1′至短幅外摆线上任意点M之间的距离;
RM——定圆圆心O至短幅外摆线上任意点M之间的距离。
所以,将式(1-21)和式(1-22)代入式(1-20),可得短幅外摆线的极坐标方程式为
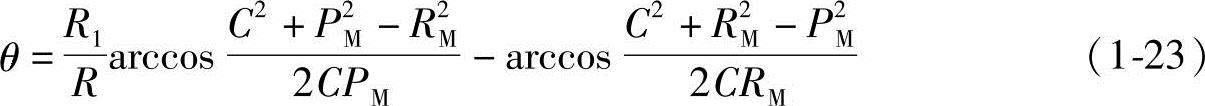
同上所述,由式(1-19)可推导得出短幅外摆线齿形曲线任意点M的直角坐标参数方程式
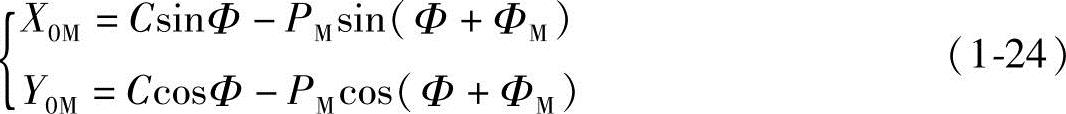
所以,极角θ也可由直角坐标得到
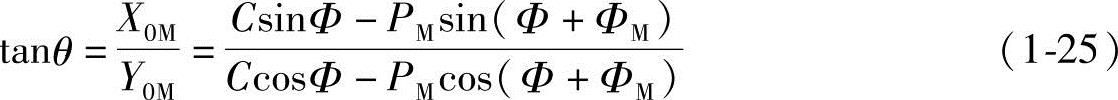
(4)内摆线齿形曲线 当半径R1的动圆O1沿半径为R的定圆O的内圆作纯滚动时,动圆O1上的点N的运动轨迹NM称为内摆线。N点即为摆点。
由图1-5可知,内摆线上任意点M的坐标值为

与外摆线同理,对于内摆线上任意点M,O1′M=R1,并将O1′M用PM表示,可得
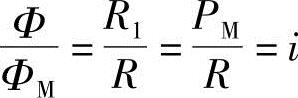
因为Φ=iΦM
θ=θ+Φ-Φ=θ+Φ-iΦM (1-27)
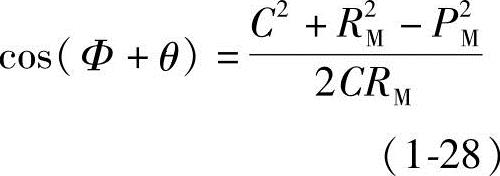
式中 C——定圆O与动圆O′1两圆心之间的距离为O1′O,C=R-R1;
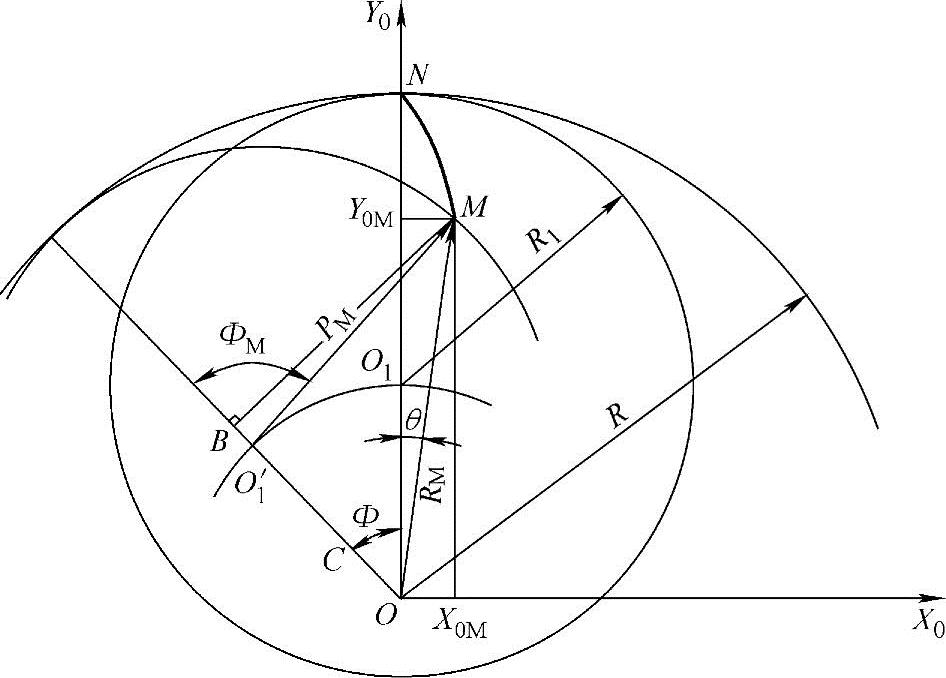
图1-5 内摆线
PM——动圆圆心O1′至内摆线上任意点M之间的距离;
RM——定圆圆心O至内摆线上任意点M之间的距离。
由图1-5中△OMB和△O1′MB可得
R2M=P2Msin2ΦM+(C+PMcosΦM)2=P2M+C2+2CPMcosΦM

将式(1-28)和式(1-29)代入式(1-27),可推得内摆线的极坐标方程式为
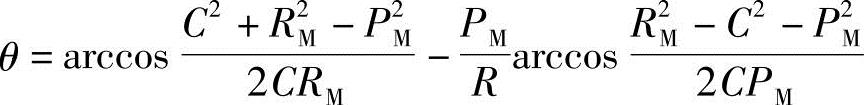
由△OMO1′和△O1MB可得
RMsin(Φ+θ)=PMsinΦM (1-30)
RMcos(Φ+θ)=C+PMcosΦM (1-31)
将式(1-30)、式(1-31)代入式(1-26),可得内摆线齿形曲线任意点M的直角坐标参数方程式:
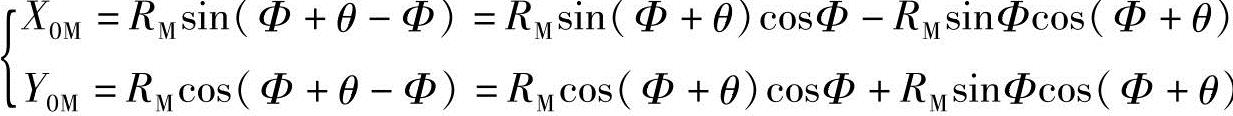
即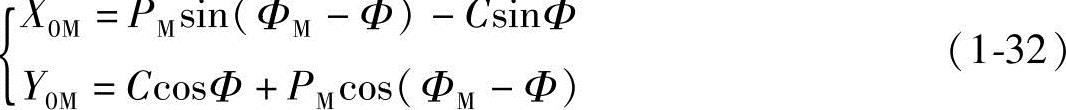
所以,极角θ也可由直角坐标得到:
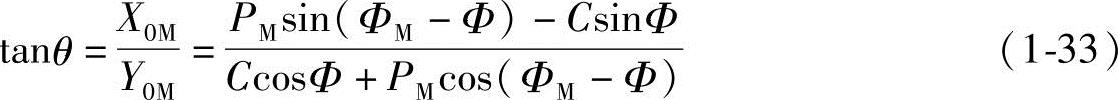
同理也可类推得长幅内摆线和短幅内摆线的有关方程式,在此就不再赘述。
(5)坐标系转换 由图1-2、图1-3、图1-4和图1-5可知,上述几种摆线上的任意点M的坐标值均是在X0OY0坐标系中,齿形曲线的起点通过Y0轴。实际上,螺杆泵螺旋面的齿形曲线大都是由多段曲线组合而成,各段曲线的起点和极角θ都不相同,为使齿形曲线有共同的坐标系,就需要规定共同的坐标系XOY。因此,各段曲线的起点N到坐标系旋转后的共同坐标系XOY的Y轴之间就有一角度θ0(Y轴就是各段曲线共同的纵轴)。通过这样的坐标旋转后,齿形曲线上任意点M到Y轴之间的极角就由原来的θ角变成了θ+θ0。显然,转换到共同坐标系XOY中的坐标值,由式(1-1)、式(1-12)、式(1-19)和式(1-26)变为

所以,从式(1-34)可推得坐标系旋转了θ0角后的直角坐标参数方程式,对于外摆线为
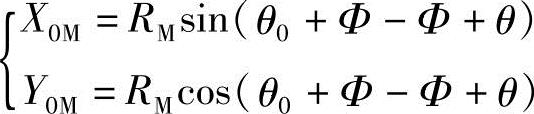
即: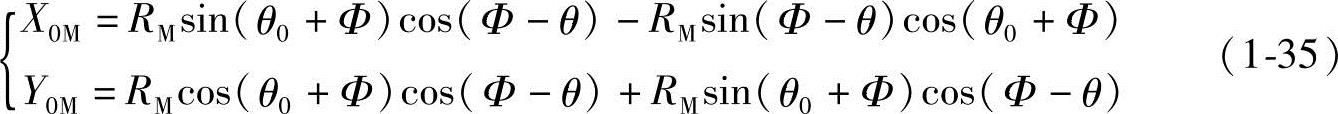
将式(1-8)和式(1-9)代入式(1-35),得
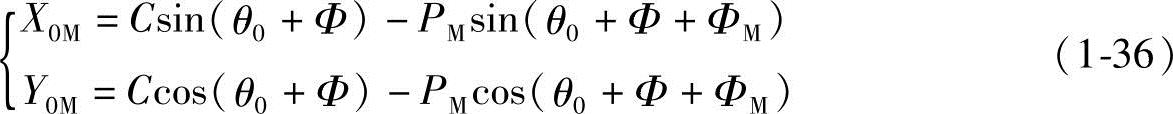
所以,极角θ也可由直角坐标得到:
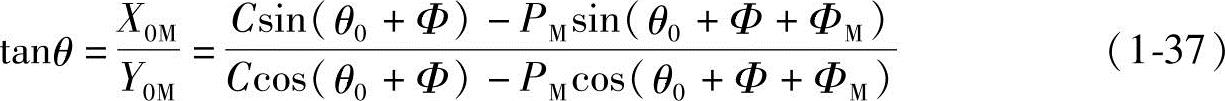
可见用极坐标参数方程式(1-6)和式(1-34)比用直角坐标参数方程式求极角θ和坐标值X0M、Y0M要方便。
同理可推得长幅外摆线的坐标系转了θ0角后的直角坐标参数方程式为
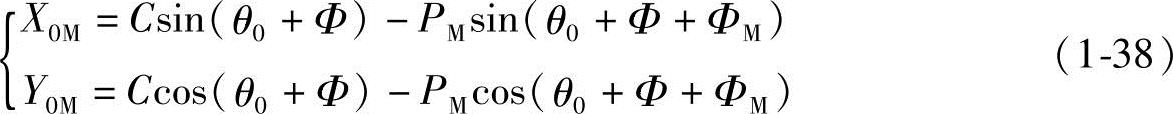
极角θ也可由直角坐标得到:
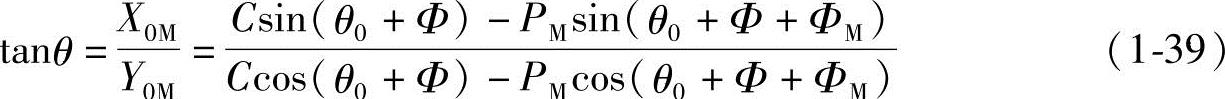
短幅外摆线的坐标系转了θ0角后,其直角坐标参数方程式为
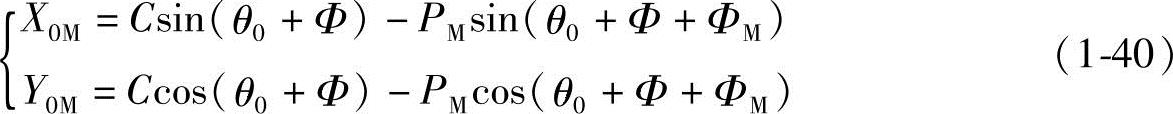
极角θ为
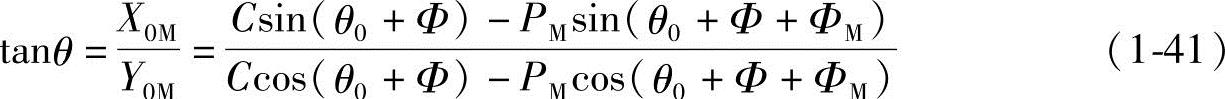
内摆线的坐标系转了θ0角后,其直角坐标参数方程式为
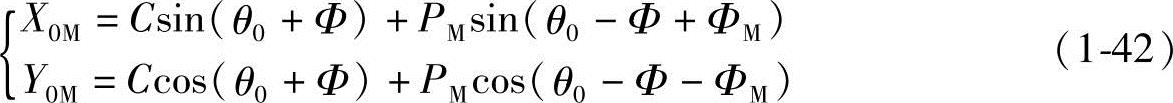
极角θ为
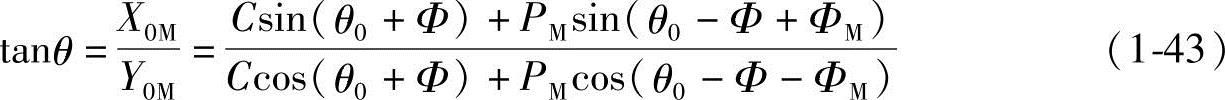
同理也可得到长幅内摆线和短幅内摆线的有关方程式,在此不再赘述。
若上述各种摆线其动圆滚动的方向相反,则这些方程式中的有关正负符号均需作相应改变。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




