在本书的第5章中已经建立了各性能参数的谐波模型，基于该模型以及电流谐波与开关角的映射关系，可以分析开关角对各性能参数的影响，分析流程如图6.9所示。
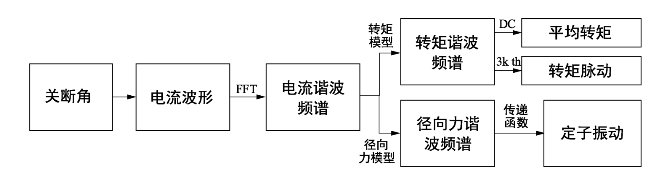
图6.9 基于谐波模型分析关断角与性能参数关系的流程
根据图6.9所示的分析流程，对1 200 r/min、6 N·m负载下的性能指标进行分析。图6.10给出了该工况下各性能参数随开关角的变化。由于不同模态的振动根源不同，即敏感谐波频率不同，选取多个径向力的谐波分量进行比较，包括径向力的5阶分量、10阶分量和15阶分量。在恒转矩约束下，转矩脉动和RMS电流随关断角的提前一直增大，5阶径向力随关断角的提前逐渐降低，而10阶径向力和15阶径向力则在达到最小值后开始增大。通过比较可以看出，各性能参数随开关角的变化并不一致。
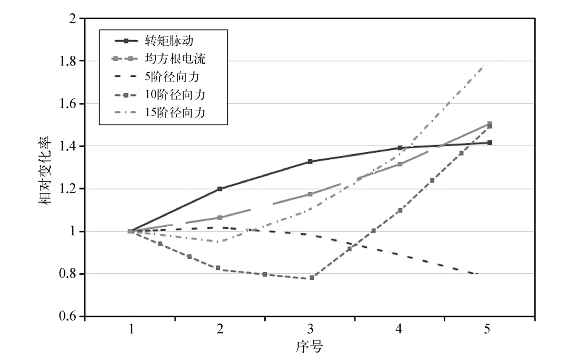
图6.10 性能参数随开关角的变化（转矩为10 N·m，转速为1 200 r/min）
在谐波模型下，各性能参数可以表示为开关角的函数，函数的导数则可以表示开关角对性能参数的影响，以径向力为例：
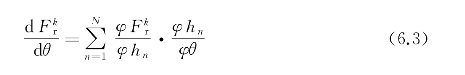(www.xing528.com)
式中，
表示第k阶径向力，hn表示第n阶电流谐波的幅值，θ表示关断角。由式（6.3）可知，开关角对性能参数的影响由两部分表征：一是电流谐波对性能参数的影响，即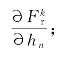
二是开关角对电流谐波的影响，即
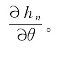图6.11给出各性能参数对谐波分量的偏导数
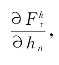偏导数可以表示一个函数对某个自变量变化的敏感度，偏导数越大，自变量的变化对函数值影响越大。
通过图6.11可以得到以下结论。
（1）转矩脉动和RMS电流对低阶谐波的偏导数更大，即对低阶谐波的变化更敏感。
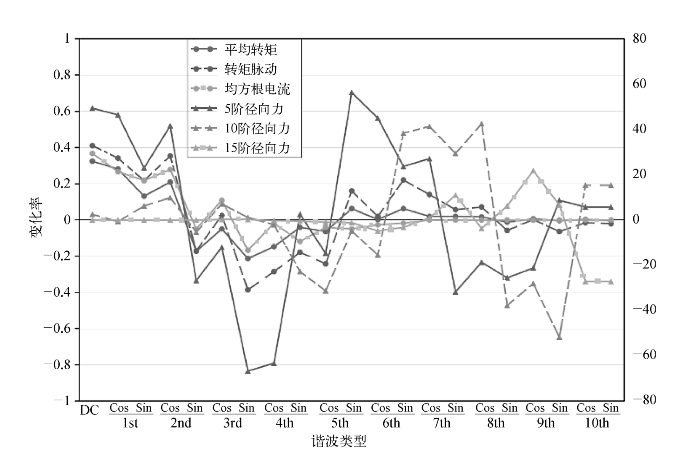
图6.11 各性能参数对谐波分量的偏导数（转矩为10 N·m，转速为1 200 r/min）
（2）不同阶的径向力敏感范围不同，5阶径向力对2～7阶的电流谐波更敏感，10阶径向力对6～9阶的电流谐波更敏感，15阶径向力对8～10阶的电流谐波更敏感。
（3）低阶径向力与转矩脉动和RMS电流的敏感范围重合度高，耦合更加明显。低阶电流谐波的变化会同时引起转矩脉动、RMS电流和低阶径向力的变化。
（4）当径向力的导数与其他性能指标的导数同符号时，径向力的优化与其他目标的优化可以同时进行，即通过调整某一谐波成分可以同时降低转矩脉动、径向力和RMS电流；反之亦然。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
