电流谐波分量与性能指标的关系

文献［6］研究了恒参考电流驱动方式下不同阶次电流谐波对转矩及转矩脉动的影响，指出电流的直流分量、1阶分量和2阶分量对平均转矩的贡献最大，而电流的3阶分量和4阶分量对平均转矩影响不大，但对转矩脉动影响较大。参照该文献的做法，本节对恒参考电流驱动方式下不同阶次电流谐波对径向力及振动的影响进行了研究。

在恒参考电流控制模式下，电流的波形近似为梯形波，首先对其进行傅里叶分解，得到电流波形的谐波频谱。电流谐波成分主要受开通角、关断角及参考电流的影响，以开通角和关断角分别为25°和140°（均为电角度）、参考电流为2 A的电流波形为例，各阶次电流谐波的幅值和相位如表5.1所示。

表5.1　电流波形谐波（开关角为25°～140°，参考电流为2 A）

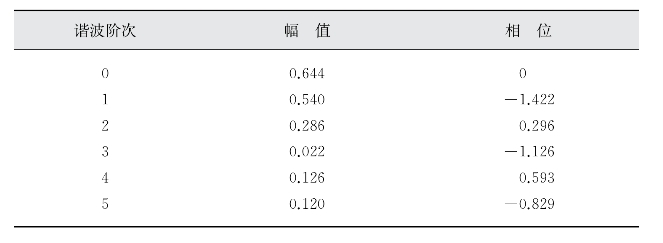
为了评价不同电流谐波对振动的影响，本节将不同谐波电流驱动下的径向力与恒参考电流下的径向力进行对比。首先将电流谐波进行组合，从最简单的直流成分＋1阶谐波开始，依次增加谐波成分，得到不同组合方式。根据不同组合方式下的电流波形，结合径向力-电流-位置的函数关系，通过查表的方法可以获得特定电流波形对应的径向力波形，再通过对径向力波形的分解可以获得径向力的谐波成分。通过对不同组合方式下径向力谐波成分的对比可以看出，不同阶次电流谐波对径向力的“贡献”。分析流程如图5.1所示。

本节对5种不同电流组合方式下的径向力谐波成分进行了对比，5种组合方式分布如表5.2所示。

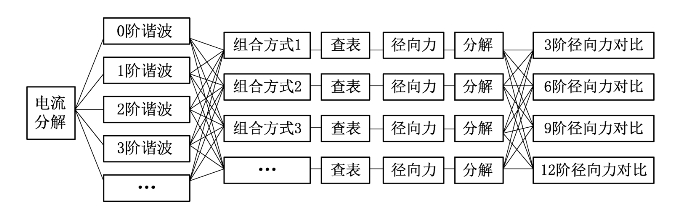
图5.1　电流谐波与径向力关联性分析流程

表5.2　电流谐波组合方式

(www.xing528.com)

表5.2所示的5种组合方式中，谐波分量的幅值和相位按照表5.1所给的各阶电流分量的幅值和相位设置。

由径向力-振动的传递函数知，对振动起作用的是某阶次的径向力谐波，且不同模态下起主导作用的径向力谐波阶次不同。根据开关磁阻电机的振动频谱，0阶模态的振动幅值较大，对于三相开关磁阻电机，考虑到不同相间径向力的叠加作用，在0阶模态下，3倍频径向力谐波为振动的主要来源，因此重点分析不同组合方式下3倍频径向力谐波的变化规律，3阶径向力谐波、6阶径向力谐波、9阶径向力谐波和12阶径向力谐波在5种组合方式下的幅值如图5.2所示。

根据图5.2可以得出以下结论。

（1）对于径向力的3阶谐波分量，在组合方式2（DC＋1st）下的幅值明显小于其他方式下的幅值，组合方式1、3、4、5的幅值接近，说明3阶电流谐波分量对3阶径向力谐波的贡献较大［见图5.2（a）］。

（2）对于径向力的6阶谐波分量，在组合方式2（DC＋1st）、3（DC＋1st＋2nd）、4（DC＋1st＋2nd＋3rd）下的幅值明显小于其他方式下的幅值，组合方式1的幅值最大，说明4阶及以上电流谐波分量对6阶径向力谐波的贡献较大［见图5.2（b）］。

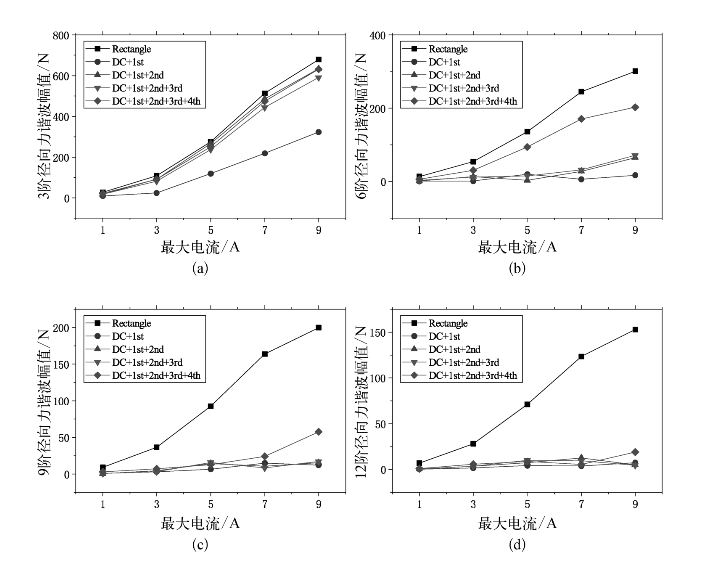
图5.2　不同电流组合方式下径向力谐波变化规律

（3）对于径向力的9阶和12阶谐波分量，在组合方式2（DC＋1st）、3（DC＋1st＋2nd）、4（DC＋1st＋2nd＋3rd）、5（DC＋1st＋2nd＋3rd＋4th）下的幅值均较小，远小于组合方式1的幅值，说明9阶和12阶径向力谐波主要由5阶及以上电流谐波产生［见图5.2（c）和（d）］。

（4）径向力的幅值随阶数的升高而降低。

根据上述分析可知，可以通过限制最高电流谐波频次的方式降低径向力，且径向力阶数越低，需要限制的电流谐波成分越多。考虑到电流谐波与转矩的关系，将电流谐波最高频次限制在2阶既可以保证足够的转矩能力，同时也有较好的降低径向力的作用。