开关磁阻电机定子绕组静态模型优化

开关磁阻电机（SRM）工作时遵循磁阻最小原理，即沿最小磁阻路径闭合的磁通使得磁场扭曲，由此产生使转子旋转的切向力。当其转子与定子在极对位时，SRM存在严重的磁路饱和问题。SRM的磁场是转子位置角和定子绕组相电流的非线性函数，因此需建立定子工作状态的电气模型分析SRM的电感特性。

图4.1　SRM定子绕组电流工作回路

由SRM工作原理可知，定子绕组在工作时分为励磁和退磁两个阶段，SRM单相工作时的不对称半桥型主回路如图4.1所示。

在开关K1、K2导通瞬间，电源正向加载在绕组两端，绕组开始励磁，相电流从零开始递增，电流从电源处通过功率开关流向绕组，在K1、K2关断前，绕组相电流从零遍历到最大值；在功率开关K1、K2断开瞬间，电源电压反向加载在绕组电感两端，绕组开始退磁，相电流开始减小，此时回路中的电流从绕组经二极管流向电源，绕组相电流从最大值遍历到零。

首先分析励磁阶段的定子绕组磁场，合理忽略各项间磁场耦合的影响，可得励磁阶段SRM的单相电压平衡方程为

式中，U为绕组相电压，R为绕组相电阻，i为绕组相电流，ψ为绕组相磁链。等式右边第一项Ri为绕组的电阻压降，第二项为绕组的电感压降。

绕组磁链ψ为绕组电流i和转子位置角θ的函数，且磁链对相电流的偏导数为绕组电感，即

(www.xing528.com)

又由式（4.1）和式（4.3）得到新的电路方程，即式（4.4）右边第一项为绕组线圈的电阻压降，第二项为绕组中电感的感抗压降，第三项为绕组中的磁场由位移改变而产生的反电动势［12］。

当固定SRM转子的位置角为θ0时，转子的角速度ω＝0，等式第三项的反电动势为零，电源电压只用来克服绕组的电阻压降和感抗压降。由此可得，当转子固定在某一位置角（θ＝θ0）时，磁链和电感成为绕组相电流的一元函数，所以绕组的电感可表示为

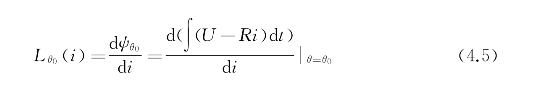
由此可知在励磁阶段，当SRM的转子固定在θ0时，绕组磁链值为绕组的电感端电压对时间的积分，并通过磁链对电流的求导可得该位置（θ＝θ0）时SRM的电感-电流曲线。

相应地可以推得该位置角处（θ＝θ0）退磁阶段的电感计算公式。在SRM的退磁阶段，电源的电压反向加载在绕组相的两端，即此时绕组的相电压为－U。绕组中相电流的流向并没有改变，但其值由峰值逐渐减小，并产生与励磁阶段方向相反的感应电动势。所以退磁时SRM的单相电路方程为

相应地可以导出在位置角为θ0时，退磁阶段的电感计算式为

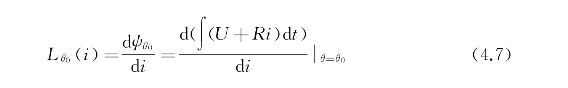
当向电机绕组加一遍历电流时，通过式（4.5）或式（4.7）可以计算得到位置角为θ0时的电感-电流曲线。在不同的位置角（θ＝θ1，θ2，θ3，θ4…）固定电机转子，通过重复上述电流遍历测量，可得到整个电气周期内不同位置角处的电感-电流曲线，即可以得到电感相对位置角和相电流的模型。